Física/Texto completo
Introducción a la Física
Definición de la Física
La Física es la ciencia dedicada al estudio de las fuerzas que se dan en la naturaleza, en el más amplio sentido de la búsqueda del conocimiento.
También la Física es una ciencia natural que estudia las propiedades del espacio, el tiempo, la materia, la energía y sus interacciones. La Física es la ciencia dedicada al estudio de los fenómenos naturales.
Historia de la Física
Desde la más remota antigüedad las personas han tratado de comprender la naturaleza y los fenómenos que en ella se observan: el paso de las estaciones, el movimiento de los cuerpos y de los astros, los fenómenos climáticos, las propiedades de los materiales, etc. Las primeras explicaciones aparecieron en la Antigüedad y se basaban en consideraciones puramente filosóficas, sin verificarse experimentalmente. Algunas interpretaciones falsas, como la hecha por Ptolomeo en su famoso "Almagesto" - "La Tierra está en el centro del Universo y alrededor de ella giran los astros" - perduraron durante siglos.
La física es una de las más antiguas disciplinas académicas, tal vez la más antigua a través de la inclusión de la astronomía. En los últimos dos milenios, la física había sido considerada sinónimo de la filosofía, la química, y ciertas ramas de la matemática y la biología, pero durante la Revolución Científica en el siglo XVII surgió para convertirse en una ciencia moderna, única por derecho propio. Sin embargo, en algunas esferas como la física matemática y la química cuántica, los límites de la física siguen siendo difíciles de distinguir.
La revolución científica post-renacentista
En el Siglo XVI Galileo Galilei fue pionero en el uso de experiencias para validar las teorías de la Física. Se interesó en el movimiento de los astros y de los cuerpos. Usando instrumentos como el plano inclinado, descubrió la ley de la inercia de la dinámica, y con el uso de uno de los primeros telescopios observó que Júpiter tenía satélites girando a su alrededor y las manchas solares del Sol. Estas observaciones demostraban el modelo heliocéntrico de Nicolás Copérnico y el hecho de que los cuerpos celestes no son perfectos. En la misma época, las observaciones de Tycho Brahe y los cálculos de Johannes Kepler permitieron establecer las leyes que gobiernan el movimiento de los planetas en el Sistema Solar.
En 1687 Isaac Newton publicó los Principios Matemáticos de la Naturaleza, una obra en la que se describen las leyes clásicas de la dinámica conocidas como: Leyes de Newton; y la ley de la gravitación universal de Newton. El primer grupo de leyes permitía explicar la dinámica de los cuerpos y hacer predicciones del movimiento y equilibrio entre ellos, la segunda ley permitía demostrar las leyes de Kepler del movimiento de planetas y explicar la gravedad terrestre (de aquí el nombre de gravedad universal). En esta época se puso de manifiesto uno de los principios básicos de la Física, las leyes de la Física son las mismas en cualquier punto del Universo. El desarrollo por Newton y Leibniz del cálculo matemático proporcionó las herramientas matemáticas para el desarrollo de la Física como ciencia capaz de realizar predicciones. En esta época desarrollaron sus trabajos físicos como Robert Hooke y Christian Huygens estudiando las propiedades básicas de la materia y de la luz.
A finales del siglo XVII la física comienza a influenciar el desarrollo tecnológico permitiendo a su vez un avance más rápido de la propia física. El desarrollo instrumental (telescopios, microscopios y otros instrumentos) y el desarrollo de experimentos cada vez más sofisticados permitieron obtener grandes éxitos como la medida de la masa de la Tierra en el experimento de la balanza de torsión. También aparecen las primeras sociedades científicas como la Royal Society en Londres en 1660 y la Académie des Sciences en París en 1666 como instrumentos de comunicación e intercambio científico, teniendo en los primeros tiempos de ambas sociedades un papel preeminente las ciencias físicas.
Siglo XVIII: Termodinámica y óptica
A partir del Siglo XVIII Robert Boyle, Thomas Young y otros desarrollaron la termodinámica. En 1733 Daniel Bernoulli usó argumentos estadísticos, junto con la mecánica clásica, para extraer resultados de la termodinámica, iniciando la mecánica estadística. En 1798 Benjamin Thompson demostró la conversión del trabajo mecánico en calor y en 1847 James Prescott Joule formuló la ley de conservación de la energía.
En el campo de la óptica el siglo comenzó con la teoría corpuscular de la luz de Isaac Newton expuesta en su famosa obra Opticks. Aunque las leyes básicas de la óptica geométrica habían sido descubiertas algunas décadas antes el siglo XVIII fue rico en avances técnicos en este campo produciéndose las primeras lentes acromáticas, midiéndose por primera vez la velocidad de la luz y descubriendo la naturaleza espectral de la luz. El siglo concluyó con el célebre experimento de Young de 1801 en el que se ponía de manifiesto la interferencia de la luz demostrando la naturaleza ondulatoria de ésta.
El siglo XIX: Electromagnetismo y la estructura de la materia
La investigación física de la primera mitad del siglo XIX estuvo dominada por el estudio de los fenómenos de la electricidad y el magnetismo. Coulomb, Luigi Galvani, Michael Faraday, Georg Simon Ohm y muchos otros físicos famosos estudiaron los fenómenos dispares y contraintuitivos que se asocian a este campo. En 1855 James Clerk Maxwell unificó las leyes conocidas sobre el comportamiento de la electricidad y el magnetismo en una sola teoría con un marco matemático común mostrando la naturaleza unida del electromagnetismo. Los trabajos de Maxwell en el electromagnetismo se consideran frecuentemente equiparables a los descubrimientos de Newton sobre la gravitación universal y se resumen con las conocidas, ecuaciones de Maxwell, un conjunto de cuatro ecuaciones capaz de predecir y explicar todos los fenómenos electromagnéticos clásicos. Una de las predicciones de esta teoría era que la luz es una onda electromagnética. Este descubrimiento de Maxwell proporcionaría la posibilidad del desarrollo de la radio unas décadas más tarde por Heinrich Rudolf Hertz en 1888.
En 1895 Wilhelm Röntgen descubrió los rayos X, ondas electromagnéticas de frecuencias muy altas. Casi simultáneamente, Henri Becquerel descubría la radioactividad en 1896. Este campo se desarrolló rápidamente con los trabajos posteriores de Pierre Curie, Marie Curie y muchos otros, dando comienzo a la física nuclear y al comienzo de la estructura microscópica de la materia. En 1897 Joseph John Thomson descubrió el electrón, la partícula elemental que transporta la corriente en los circuitos eléctricos proponiendo en 1904 un primer modelo simplificado del átomo.
El siglo XX: La segunda revolución de la física
El siglo XX estuvo marcado por el desarrollo de la física como ciencia capaz de promover el desarrollo tecnológico. A principios de este siglo los físicos consideraban tener una visión cuasi completa de la naturaleza. Sin embargo pronto se produjeron dos revoluciones conceptuales de gran calado: El desarrollo de la teoría de la relatividad y el comienzo de la mecánica cuántica.

En 1905 Albert Einstein formuló la teoría de la relatividad espacial, en la cual el espacio y el tiempo se unifican en una sola entidad, el espacio-tiempo. La relatividad formula ecuaciones diferentes para la transformación de movimientos cuando se observan desde distintos sistemas de referencia inerciales a aquellas dadas por la mecánica clásica. Ambas teorías coinciden a velocidades pequeñas en relación a la velocidad de la luz. En 1915 extendió la teoría espacial de la relatividad para explicar la gravedad, formulando la teoría general de la relatividad, la cual sustituye a la ley de la gravitación de Newton.
En 1911 Ernest Rutherford dedujo la existencia de un núcleo atómico cargado positivamente a partir de experiencias de dispersión de partículas. A los componentes de carga positiva de este núcleo se les llamó protones. Los neutrones, que también forman parte del núcleo pero no poseen carga eléctrica, los descubrió James Chadwick en 1932.

En los primeros años del Siglo XX Max Planck, Albert Einstein, Niels Bohr y otros desarrollaron la teoría cuántica a fin de explicar resultados experimentales anómalos sobre la radiación de los cuerpos. En esta teoría, los niveles posibles de energía pasan a ser discretos. En 1925 Werner Heisenberg y en 1926 Erwin Schrödinger y Paul Dirac formularon la mecánica cuántica, en la cual explican las teorías cuánticas precedentes. En la mecánica cuántica, los resultados de las medidas físicas son probabilidad|probabilísticos; la teoría cuántica describe el cálculo de estas probabilidades.
La mecánica cuántica suministró las herramientas teóricas para la física de la materia condensada, la cual estudia el comportamiento de los sólidos y los líquidos, incluyendo fenómenos tales como estructura cristalina, semiconductividad y superconductividad. Entre los pioneros de la física de la materia condensada se incluye Felix Bloch, el cual desarrolló una descripción mecano-cuántica del comportamiento de los electrones en las estructuras cristalinas (1928).
La teoría cuántica de campos se formuló para extender la mecánica cuántica de manera consistente con la teoría especial de la relatividad. Alcanzó su forma moderna a finales de los 1940s gracias al trabajo de Richard Feynman, Julian Schwinger, Tomonaga y Freeman Dyson. Ellos formularon la teoría de la electrodinámica cuántica, en la cual se describe la interacción electromagnética.
La teoría cuántica de campos suministró las bases para el desarrollo de la física de partículas, la cual estudia las fuerzas fundamentales y las partículas elementales. En 1954 Yang Chen Ning y Robert Mills desarrollaron las bases del modelo estándar. Este modelo se completó en los años 1970 y con él se describen casi todas las partículas elementales observadas.
La física en los albores del Siglo XXI
La física sigue enfrentándose a grandes retos, tanto de carácter práctico como teórico, a comienzos del siglo XXI. El estudio de los sistemas complejos dominados por sistemas de ecuaciones no lineales, tal y como la meteorología o las propiedades cuánticas de los materiales que han posibilitado el desarrollo de nuevos materiales con propiedades sorprendentes. A nivel teórico la astrofísica ofrece una visión del mundo con numerosas preguntas abiertas en todos sus frentes, desde la cosmología hasta la formación planetaria. La física teórica continúa sus intentos de encontrar una teoría física capaz de unificar todas las fuerzas en un único formulismo en lo que sería una teoría del todo. Entre las teorías candidatas debemos citar la teoría de supercuerdas.
División de la Física
La Física se divide para su estudio en dos grandes grupos, la física clásica y la física moderna. La física clásica no tiene en cuenta los efectos relativistas, descubiertos por Einstein, ni los efectos cuánticos, considerando la constante de Plank nula. La física moderna sí tiene en cuenta estos factores, dando lugar a la física relativista y a la física cuántica.
Física Teórica
Esta es una introducción a la física teórica la cual pueden encontrar en muchos libros aquí en wikibooks. Pero esta ese una manera mas fácil para entender a la física, desde una perspectiva teórica.
La física teórica se aprende en la Universidad y su estudio supone algún conocimiento previo de: física experimental, análisis matemático, álgebra vectorial, análisis vectorial y ecuaciones diferenciales sencillas.
La Física comienza con la cuidadosa observación de fenómenos físicos: como en la naturaleza o en los experimentos se presentan.
La observación de tales hechos sigue con la descripción mas precisa posible. Pongamos un ejemplo sencillo: para el continuo enfriamiento de agua a hielo. Para este fenómeno no se podría hacer mas un descubrimiento trivial: para el enfriamiento el agua entrega calor. Pero de aquí cabe una pregunta: "Cuanto calor?", respuesta: "La cantidad de calor depende de la masa del agua enfriada". - Como es la conexión entre masa y cantidad de calor? - "La cantidad de calor es proporcional a la masa" - Con esto comienza la "matematizacion" de la física: "proporcional" es un concepto matemático. Eso significa aqui, que el cociente entre la cantidad de calor y la masa siempre tiene el mismo valor. - Para finalizar se puede definir un nuevo concepto: el constante cociente de la cantidad de calor y la masa se lo llama "calor especifico" del agua en este caso. Pero con esto viene una nueva pregunta: " Tienen todas las sustancias el mismo calor especifico?" - Ni por coincidencia! - Después: "Es posible, el calor del agua - también la energía - transferirla y de donde proviene?" - y con eso estamos frente a una típica pregunta de la física teórica, que finalmente proviene de la teoría cinética del calor.
Ejemplo de una extraordinaria historia real
El astrónomo danés Tycho Brahe (1546-1601), el importante observador que perfeccionó el telescopio, observó como unos cuatro años la posición de los planetas desde un segundo plano a una parte del cielo fija y tomando precisas anotaciones sobre eso. Con los datos de esas anotaciones, Johannes Kepler (1571-1630) pudo deducir el movimiento planetario, una verbal-matemática descripción de los hechos. Lo que descubrió fue que:
- Los planetas se mueven en trayectorias elípticas, donde en uno de sus focos esta el Sol.
- El radio vector, la linea que une al Sol y a un planeta, cubre en el mismo tiempo el mismo espacio.
- La segunda potencia de un periodo de revolución de los planetas se comporta como la tercera potencia del gran semieje de su dirección elíptica.
La extracción de esos datos de Tycho Brahe no es siempre descrito en la Física, pese a que es un dato relevante. Sobre eso también se preguntó Kepler, sobre la causa física del movimiento y sus leyes. (La escolástica de la edad media aceptaba aun, que los planetas eran dirigidos por los ángeles por sus recorridos hacia la Tierra) El supuso que entre los planetas y el Sol - sobretodo entre dos masas - debería haber una fuerza atrayente.
Tycho Brahe fue aquí solo el observador, Johannes Kepler el interprete y el primer interlocutor de la razón física del movimiento planetario.
A partir de las leyes de Kepler, Isaac Newton (1643-1727), pudo deducir las leyes de la Gravitación: entre dos masas opera una fuerza de atracción, que es proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia. Issac Newton hizo aquí de físico teórico.
Un triunfo de la física teórica fue también que en 1846 el astrónomo Johann Galle pudiera descubrir el planeta Neptuno, después de que Urbain Le Verrier calculo su posición por la interferencia del camino del planeta Urano.
A la genialidad del físico teórico pertenecen también, que si antes se hubiera deducido la desconocida (o no clara) consecuencia de su resultado, la experiencia podría ponerse a prueba nuevamente. Ahi un impresionante ejemplo: Albert Einstein baso su Teoria de la Relatividad General del conocido, pero no claro hecho, que un cuerpo en caída libre es ingrávido, que significa, que masas pesadas y lentas deben ser proporcionales a sus cuerpos. Como consecuencia de su teoría resulto la conocida, pero no clara, movimiento de perihelio de Mercurio, cuyo camino elíptico rota alrededor del Sol.
Todo el mundo se fue en contra de la Teoría de la Relatividad General de Einstein cuando dijo que se producía una curvatura en un rayo de luz que pasa junto a las cercanías del Sol. Ese efecto puede ser observado en eclipses reales de Sol.
Para terminar un ultimo indicación de los significados "prácticos" de la física teórica: La moderna y complicada tecnología de ahora seria inconcebible sin la física teórica. ¡No hay nada practico sin una buena teoría!.
Concepto de Modelo
La Física utiliza modelos matemáticos para describir los fenómenos naturales. Es decir, que las leyes y principios que enuncia son sólo aproximaciones y no algo preciso.
Los físicos observan un fenómeno, acumulan datos y luego intentan formular una expresión matemática, generalmente basadas en conocimientos anteriores, que se adecue a los datos experimentales. Para hacer un modelo necesitas observar a la naturaleza y así entender más de los fenómenos.
Para mayor información ver:
Unidades y medidas
Cantidades dimensionales
Corresponden a ciertas magnitudes que están asociadas a las dimensiones. Se miden en unidades de longitud, área, tiempo, espacio, etc.
Cantidades adimensionales
Corresponden a magnitudes que pueden ser expresadas sin necesidad de una unidad de medida, pueden ser cocientes entre cantidades dimensionales. Ejemplo de estas son los grados de un ángulo o también las constantes, como la relación de la masa entre protón y electrón.
Magnitud
Se llama magnitud a la propiedad de la física que es medida. Pueden ser clasificadas en dos clases:
- magnitudes fundamentales y
- magnitudes derivadas
Magnitudes fundamentales
Son aquellas que se definen en función de otras magnitudes físicas y que sirven de base para obtener las demás magnitudes utilizadas en la física. Son las que no derivan de otras, única es su especie, son el cimiento de la física, y no se pueden ni multiplicar o dividir entre otras.
Magnitudes derivadas
Son las que resultan de multiplicar o dividir entre si las magnitudes fundamentales.
Medir
Medir es comparar una magnitud con otra que se utiliza como patrón. Este patrón es una magnitud de valor conocido y perfectamente definido que se usa como referencia para la medida. Así, cuando medimos una distancia, el patrón sería la cinta métrica, y la medida sería el resultado de comparar la distancia que estamos midiendo, con la cinta métrica.
Sistemas de medidas
Un sistema de medidas es un conjunto que consiste en unidades de medida. Definen un conjunto básico de unidades de medida a partir del cual se derivan el resto. Existen varios sistemas de unidades:
Sistema Métrico Decimal
El primer sistema de unidades bien definido que hubo en el mundo fue el Sistema Métrico Decimal, implantado en 1795 como resultado de la Convención Mundial de Ciencia celebrada en París, Francia; este sistema tiene una división decimal y sus unidades fundamentales son: el metro, el kilogramo-peso y el litro.
Sistema MKS
Tiene su origen en 1902 de la mano del ingeniero italiano Giovani Giorgi siendo adoptado por la Comisión Electrotécnica Internacional en París en el año 1935. Este sistema también recibe el nombre de MKS, cuyas iniciales corresponden al metro, al kilogramo y al segundo como unidades de longitud, masa y tiempo respectivamente.
Sistema Usual en Estados Unidos (EIA)
Se basa en el sistema inglés, y es muy familiar para todos en Estados Unidos. Usa el pie como unidad de longitud, la libra como unidad de peso o fuerza, y el segundo como unidad de tiempo. En la actualidad, el SUEU está siendo sustituido rápidamente por el sistema internacional, en la ciencia, la tecnología, y en algunos deportes.
Debido a que en el mundo científico se buscaba un solo sistema de unidades que resultara práctico, claro y de acuerdo con los avances de la ciencia. En 1960 científicos y técnicos de todo el mundo se reunieron en Ginebra, Suiza, y acordaron adoptar el llamado Sistema Internacional de Unidades (SI).
Este sistema se basa en el llamado MKS. El Sistema Internacional tiene como magnitudes y unidades fundamentales las siguientes: para longitud el metro (m), para masa el kilogramo (kg), para tiempo el segundo (s), para temperatura al Kelvin (K), para intensidad de corriente eléctrica al ampere (A), para la intensidad luminosa la candela (cd) y para cantidad de sustancia el mol
Unidades
Las unidades del Sistema Internacional de Unidades fueron fijadas en la XI Conferencia General de Pesas y Medidas de París (1960).
| Magnitud | Unidades | Dimensión | Simbolo | Descripción |
|---|---|---|---|---|
| Longitud | Metro | L | m | Unidad de longitud, se definió originalmente como la diezmillonésima parte del cuadrante del meridiano terrestre. Más tarde se estableció un metro patrón de platino iridiado que se conserva en París. En la actualidad, el metro se define como la longitud igual a 1.650.763,73 longitudes de onda, en el vacío, de la radiación correspondiente a la transición entre los niveles 2p10 y 5d5, del átomo de criptón 86. Ahora se define al metro como la longitud de la trayectoria recorrida por la luz en el vacío durante un intervalo de tiempo de 1/299,792,458 de segundo. |
| Masa | Kilogramo | m | Kg | Unidad de masa, es la masa de un cilindro de platino iridiado establecido en la III Conferencia General de Pesas y Medidas de París. También se define al gramo (milésima parte del kilogramo) como la masa de un centímetro cúbico de agua destilada cuando tiene la mayor densidad, esto sucede a cuatro grados centígrados. |
| Tiempo | Segundo | t | s | Unidad de tiempo, originalmente, el segundo fue definido como 1/86400 del día solar medio. Se llama día solar verdadero el tiempo transcurrido entre dos pasos consecutivos del Sol por el meridiano de un lugar; pero como no todos los días son de igual duración en el transcurso de un año, se toma un día ficticio, llamado día solar medio, cuya duración es tal que, al cabo del año, la suma de todos estos días ficticios es la misma que la de los días reales. Actualmente se define como la duración de 9.192.631.770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133. |
| Intensidad de corriente eléctrica | Amperio | A | A | Es la intensidad de corriente eléctrica constante que, mantenida en dos conductores paralelos rectilíneos, de longitud infinita, de sección circular despreciable y colocados en el vació a uno contra otro a una distancia de un metro uno de otro, produce entre estos dos conductores una fuerza igual a 2x10-7 newton por metro de longitud.[1] |
| Temperatura termodinámica | Kelvin | θ | K | Es la unidad de temperatura termodinámica, es la fracción 1/273,16 de la temperatura termodinámica del punto triple del agua. Este mismo nombre y símbolo son utilizados para expresar un intervalo de temperatura. |
| Cantidad de sustancia | mol | N | mol | Es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 0,012 kilogramo de carbono 12. |
| Intensidad luminosa | Candela | J | cd | Es la intensidad luminosa, en la dirección perpendicular de una superficie de 1/600000 metros cuadrados de un cuerpo negro a la temperatura de solidificación del platino, bajo la presión de 101.325 newton por metro cuadrado. |
Otras unidades
Newton (N)
Usado para medir la fuerza. Es una unidad derivada equivalente a la fuerza necesaria para acelerar un kilogramo de masa a un metro por segundo cada segundo, 1 kilogramo fuerza equivale a 9 newton
Joule
Un joule equivale a la cantidad de trabajo efectuado por una fuerza de 1 Newton actuando a través de una distancia de 1 metro. En 1948 el joule fue adoptado por la Conferencia Internacional de Pesas y Medidas como unidad de energía.
El joule también es igual a 1 vatio por segundo (W·s), por lo que eléctricamente es el trabajo realizado por una diferencia de potencial de 1 voltio y con una intensidad de 1 Amperio durante un tiempo de 1 segundo.
Formula despejada
Donde representa newtons; , metros; : kilogramos; : segundos.
Equivalencias:
- 1 vatio-hora = 3.600 joules.
- 1 joule = 0,24 calorías (no confundir con kcal).
- 1 caloría termoquímica (calth) = 4,184 J
- 1 Tonelada equivalente de petróleo = 41.840.000.000 joules = 11.622 kilovatio hora.
- 1 Tonelada equivalente de carbón = 29.300.000.000 joules = 8.138,9 kilovatio hora.
Referencias
Conversión de unidades en el Sistema Internacional
Longitud
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pulgada | milímetro (mm) | 25.4 |
| pulgada | metro (m) | 0.0254 |
| pie (ft) | metro (m) | 0.3047 |
| yarda (yd) | metro (m) | 0.9144 |
Área
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pie cuadrado (ft 2) | metro cuadrado | 0.09290 |
| pulgada cuadrado | milímetro cuadrado | 645.2 |
| pulgada cuadrado | metro cuadrado | 0.0000006452 |
| yarda cuadrada | metro cuadrado | 0.08361 |
Volumen
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pulgada cubica | metro cubico | 0.00001639 |
| pie cubico | metro cubico | 0.02832 |
| yarda cubica | metro cubico | 0.7646 |
| galòn (Canada) | metro cubico | 4.546 |
| galòn (Canada) | litro | 0.004546 |
| galòn (EUA) | metro cubico | 3.785 |
| galòn (EUA) | litro | 0.003785 |
Masa
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pulgada | milímetro (mm) | 25.4 |
| pulgada | metro (m) | 0.0254 |
| pie (ft) | metro (m) | 0.3047 |
| yarda (yd) | metro (m) | 0.9144 |
Fuerza
| Imperial | Internacional | Equivalencia |
|---|---|---|
| kilopontio | kilogramo | 453.6 |
| kilopontio | Newton | 4448 |
| libra | kilogramo | 0.4536 |
| libra | Newton | 4.448 |
Energía
| Imperial | Internacional | Equivalencia |
|---|---|---|
| Unidad Termica Britanica | joule | 1056 |
| Kilowatt Hora | joule | 3,600,000 |
Temperatura
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pulgada | ||
| pulgada | ||
| pie (ft) | ||
| yarda (yd) |
Presión o Tensión
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pulgada | ||
| pulgada | ||
| pie (ft) | ||
| yarda (yd) |
Momento Flexor o Tensor
| Imperial | Internacional | Equivalencia |
|---|---|---|
| pulgada | ||
| pulgada | ||
| pie (ft) | ||
| yarda (yd) |
Fuente
http://www.inti.gob.ar/cirsoc/pdf/tabla_conversion.pdf
Mecánica clásica
- Principio de conservación de la cantidad de movimiento
- Principio de conservación de la energia
- Principio de conservación del momento angular
- Descomposición de la energía cinética
- Introducción al Campo gravitatorio
- Energía potencial en un campo gravitatorio
- Leyes de Kepler
- Centro de gravedad
- Equilibrio y reposo
- Equilibrio de un sólido rígido
- Equilibrio de un punto en un campo de fuerzas
- Tipos de equilibrio
- Rozamiento
Cinemática
La cinemática es una rama de la física dedicada al estudio del movimiento de los cuerpos en el espacio, sin atender a las causas que lo producen (lo que llamamos fuerzas). Por tanto la cinemática sólo estudia el movimiento en sí, a diferencia de la dinámica que estudia las interacciones que lo producen. El Análisis Vectorial es la herramienta matemática más adecuada para ellos
En cinemática distinguimos las siguientes partes:
La magnitud vectorial de la cinemática fundamental es el "desplazamiento" , que experimenta un cuerpo durante un lapso Δt. Como el desplazamiento es un vector, por consiguiente, sigue la ley del paralelogramo, o la ley de suma vectorial. Asi si un cuerpo realiza un desplazamiento "consecutivo" o "al mismo tiempo" dos desplazamientos y , nos da un desplazamiento igual a la suma vectorial de a+b como un solo desplazamiento. ( )

Dos movimientos al mismo tiempo entran principalmente, cuando un cuerpo se mueve respecto a un sistema de referencia y ese sistema de referencia se mueve relativamente a otro sistema de referencia. Ejemplo: El movimiento de un viajero en un tren en movimiento, que esta siendo visto por un observador desde el terraplén. O cuando uno viaja en coche y observa las montañas y los árboles a su alrededor.
Observación sobre la notación: en el texto y en la ilustración se nombra a los vectores con letras negrillas y cursivas. En las fórmulas y ecuaciones, que se escriben con TeX, son vectores los que tienen una flecha sobre sus letras
Conceptos
Modelo físico: Para estudiar la realidad, los físicos se sirven de 'modelos' que, con cierta aproximación y en determinadas condiciones, corresponden con ella. Se usan para realizar cálculos teóricos. Así, puede modelizarse un balón con una esfera para, por ejemplo, calcular su volumen con cierta aproximación conociendo su radio aproximado, aunque no es exactos.
Punto: Es un modelo físico. Se refiere a un elemento de volumen despreciable (se considerará sin volumen) situado en el espacio (en 3D. Busca 'espacio euclidiano' para más detalles).
Posición: Llamamos posición de un punto a su localización con respecto a un sistema de referencia (lo que en física se llama 'observador').
Sistema de referencia: Es aquel sistema coordenado con respecto al cual se da la posición de los puntos y el tiempo (a determinadas velocidades el tiempo cambia, buscad la paradoja de los gemelos). Profundizaremos más en este tema cuando se aborde el de Movimiento relativo.
Tiempo: Por nuestro lenguaje parece complicado de definir. Los griegos dieron una solución que, por ahora, nos puede valer. Llamamos tiempo al contínuo transcurrido entre dos instantes.
Partícula puntual: Es un modelo físico. Se refiere a un elemento de tamaño diferencial (muy pequeño) y masa concentrada en su posición.
Sólido rígido o, simplemente, sólido: Es otro modelo físico. Puede definirse de varias formas. La más usada es la que lo hace como un cuerpo cuyas distancias entre partículas permanecen constantes con el tiempo. Aunque ésto no ocurre en la realidad, para esfuerzos moderados una mesa seguira siendo rígida, pero un globo puede no responder a éste modelo. Diariamente escuchamos los conceptos de rapidez y aceleración como velocidad y aceleración solamente. Pero en física la velocidad y la aceleración son vectores, por lo que es claro y necesario su diferenciación y entendimiento. De aquí en adelante (más por costumbre que por ganas) llamaremos tanto a la rapidez y a la aceleración solamente como velocidad y aceleración (a menos que se especifique lo contrario). (velocidad y rapidez no son lo mismo!) la rapidez es una magnitud escalar, en cambio la velocidad es una magnitud vectorial. Además la rapidez se define como el modulo de la velocidad.
En física, velocidad es la magnitud física que expresa la variación de posición de un objeto en función del tiempo, o distancia recorrida por un objeto en la unidad de tiempo. Se suele representar por la letra . La velocidad puede distinguirse según el lapso considerado, por lo cual se hace referencia a la velocidad instantánea, la velocidad promedio, etc. En el Sistema Internacional de Unidades su unidad es el metro por segundo ó .
En términos precisos, para definir la velocidad de un objeto debe considerarse no sólo la distancia que recorre por unidad de tiempo sino también la dirección y el sentido del desplazamiento, por lo cual la velocidad se expresa como una magnitud vectorial.
Velocidad
Si cubre una masa puntual en un punto P en un tiempo el tramo , se llamará al cociente su velocidad media en el intervalo de tiempo o en el tramo .
Se observa que aquí no es el desplazamiento, sino la longitud de arco: es el camino recorrido.
La llamamos velocidad media porque la masa puntual no se mueve por el trayecto uniforme trazado. O sea estamos tomando sólo los puntos final e inicial para hacer los cálculos.
Hagamos el trayecto como Δs (de manera diferencial, o sea infinitesimal), al igual que al intervalo de tiempo Δt. Para Δs cercano a cero (o Δt cercano a cero, que tienda a cero) el cociente Δs/Δt como valor al límite, nos da la velocidad v de la masa puntual en el punto P, así:
En el análisis se puede calcular ese valor al límite también como ds/dt. Así:
Velocidad media o velocidad promedio
La velocidad media o velocidad promedio informa sobre la velocidad en un intervalo dado. Se calcula dividiendo el desplazamiento (delta x) por el tiempo transcurrido (delta t):
Por ejemplo, si un objeto ha recorrido una distancia de 1 metro en un lapso de 31,63 segundos, el módulo de su velocidad media es:
Al módulo de la velocidad se le llama rapidez.
Velocidad vectorial
Vamos a ver ahora a una partícula, que atraviesa un espacio en una curva. Para el tiempo t se halla en P, para el tiempo t + Δt en Q. El lugar del punto esta descrito por su vector posición 'r'. Esta es una función de t y esta descrita por una función vectorial 'r'(t).
Así:
y
donde i, j y k son los vectores unitarios de los ejes de coordenadas.
El desplazamiento de la partícula en un determinado intervalo de tiempo es:
El cociente Δr/Δt es la velocidad media (vectorial) vm de la partícula en el intervalo de tiempo Δt. Es
Aquí es (mirar arriba: rapidez y aceleración) Δx/Δt la rapidez media de la partícula paralela al eje X, Δy/Δt la rapidez media paralela al eje Y y Δz/Δt la rapidez media paralela al eje Z en un intervalo Δt.
El vector resultante, del cociente Δr/Δt para Δt cercano a cero, se llama velocidad vP = v'(t) de la partícula en P o en el tiempo t.
La función vectorial v'(t) es la primera derivada de la función de posición r(t) en el tiempo.
Como se ve, son las componentes escalares del vector v(t) idénticos con la velocidad instantánea paralela a los ejes:
El recta en el punto P en la dirección del vector vP se llama La Tangente a la curva en P
Velocidad instantánea
Informa sobre la velocidad en un punto dado.
En forma vectorial, la velocidad es la derivada (tangente) del vector posición respecto del tiempo:
donde es un versor (vector de módulo unidad) de dirección tangente a la trayectoria de cuerpo en cuestión y es el vector posición, ya que en el límite los diferenciales de espacio recorrido y posición coinciden.
Unidades de velocidad
- Metro por segundo (m/s), unidad de velocidad del Sistema Internacional de Unidades
- Kilómetro por hora (km/h) (uso coloquial)
- Kilómetro por segundo (km/s) (uso coloquial)
Referencias
La aceleración es la magnitud física que mide la tasa de variación de la velocidad respecto del tiempo. Las unidades para expresar la aceleración serán unidades de velocidad divididas por las unidades de tiempo (en unidades del Sistema Internacional generalmente).
No debe confundirse la velocidad con la aceleración, pues son conceptos distintos, acelerar no significa ir más rápido, sino cambiar de velocidad.
Se define la aceleración media como la relación entre la variación o cambio de velocidad de un móvil y el tiempo empleado en dicho cambio:
Donde a es aceleración, y v la velocidad final en el instante t, la velocidad inicial en el instante t0.

La aceleración instantánea, que para trayectorias curvas se toma como un vector, es la derivada de la velocidad (instantánea) respecto del tiempo en un instante dado (en dos instantes cercanos pero diferentes el valor puede cambiar mucho):
Puesto que la velocidad instantánea v a su vez es la derivada del vector de posición r respecto al tiempo, se tiene que la aceleración vectorial es la derivada segunda respecto de la variable temporal:
aceleración
Tomemos luego una masa puntual que tiene en el punto P y en el tiempo t la velocidad v; y en el tiempo t + Δt y la velocidad v + Δv. Podemos calcular el cociente Δv/Δt como la aceleración media am de la masa puntual en el intervalo de tiempo Δt:
Para Δt cercano a cero se aspira a que ese cociente tenga un valor límite, la aceleración a de la masa puntual para el tiempo t.
Para ese valor límite, se puede simplificar:
Es el camino s descrito como una función analítica del tiempo t, así s=s(t), así es la función de velocidad v(t) la primera derivada de la función s(t) con respecto al tiempo, la función de aceleración a(t) es la segunda derivada. La derivación con respecto al tiempo se puede también escribir como un punto sobre las variables.
En sentido contrario se puede encontrar la función de velocidad y la función de la trayectoria a través de la integración:
En las integrales indefinidas de debe aumentar una constante que puede ser conocida con las condiciones iniciales del problema.
Ejemplo: aceleración constante g. Esto es, tiempo t=0 verticalmente de arriba abajo, tiene la velocidad v0 y sus coordenadas s0:
Componentes intrínsecas de la aceleración: aceleraciones tangencial y normal
Existe una descomposición geométrica útill del vector de aceleración de una partícula, en dos componentes perpendiculares: la aceleración tangencial y la aceleración normal. La primera da cuenta de cuanto varía el módulo del vector velocidad o celeridad. La aceleración normal por el contrario da cuenta de la tasa de cambio de la dirección velocidad:
Donde es el vector unitario y tangente a la trayectoria del mismo sentido que la velocidad. Usando las fórmulas de geometría diferencial de curvas se llega a que la expresión anterior es igual a:
Donde at es la aceleración tangencial, an es la aceleración normal y los vectores que aparecen en la anterior expresión se relacionan con los vectores del Triedro de Frênet-Serret que aparece en la geometría diferencial de curvas del siguiente modo:
- es el vector unitario tangente a la curva.
- es el vector normal (unitario) de la curva.
- es el vector velocidad angular que es siempre paralelo al vector binormal de la curva.
Aceleración
Análogamente vamos ahora a definir la función vectorial de la aceleración:
La función vectorial de la aceleración proviene de las componentes escalares de la función velocidad y de la función posición, así:
Como se conoce, son las componentes escalares del vector velocidad igual a la dirección de la velocidad instantánea en los ejes de coordenadas. En sentido contrario se puede hallar por integración las correspondientes funciones. Ejemplo: Para la caída libre con velocidad inicial v0 de un punto con el vector posición r0 (vertical o lanzamiento curvo). Cuando el eje Z (vector unitario k) esta dirigido verticalmente hacia abajo, es
Mientras el vector velocidad siempre tiene dirección tangencial, puede estar dirigido opcionalmente el vector aceleración. En un análisis profundo, la aceleración se descompone en dos componentes, en la una dirección es tangencial (aceleración tangencial) y la otra está en dirección vertical (aceleración normal). La aceleración tangencial cambia solo el valor de la velocidad (esta es la rapidez) Para esta descomposición de los vectores de la aceleración introducimos la curva s, este es el largo de la trayectoria, que recorre la partícula en la curva. Este arco cuenta con un punto cero escogido, que de todas formas aquí no juega ningún papel, aquí solo necesitamos el diferencial ds del arco. Además introducimos el vector unitario tangencial t y hacemos uso de la geometría diferencial. El vector unitario tangente t es el vector
así denominado, es igual al vector v dividido para su módulo v. Este módulo es igual a la rapidez y es otra vez el desplazamiento sobre la curva sobre el tiempo. Así es:
Si diferenciamos para el tiempo tenemos que
Aquí la longitud del vector unitario tangencial t es constante (cercano a 1), esta el vector desplazamiento dt/ds - cuando no es igual a cero - verticalmente hacia t.
De la geometría diferencial tenemos, que el vector desplazamiento dt/ds
- tiene la dirección del vector unitario normal n y
- el valor k = 1/ρ
De aquí es k la curvatura de la curva en el punto observado y ρ su radio de curvatura. El vector unitario normal n es dirigido hacia (momentáneamente) un punto medio de la curvatura (hacia dentro).
Siguiendo esto
Con esto nos da como resultado
El vector a está entre t y n' dirigido, en el plano de la curva en un determinado punto. El módulo de la aceleración tangencial es - como se esperaba:
el módulo de la aceleración normal es
Este par de ecuaciones tienen su interpretación: La aceleración de una partícula da lugar a la aparición de una fuerza. La dirección de esa fuerza determina la dirección de la aceleración. La componente tangencial de la aceleración causa un cambio en la velocidad, la componente normal de la aceleración causa la curvatura de la curva. El radio de curvatura de la curva en un determinado punto resulta de la aceleración normal y de la velocidad así:
Movimiento circular
Una partícula P se mueve en una circunferencia. Colocamos un eje de coordenadas XY y en el origen O del sistema de coordenadas en el centro de la circunferencia.
Entonces es
Análogo a la velocidad y a la aceleración podemos definir la velocidad angular ω así
y a la aceleración angular α
Cuando t = 0 es también φ = 0, entonces es
Movimiento circular uniforme
Un movimiento circular con velocidad angular constante se lo llama uniforme. Entonces
La ecuación del vector posición es
Con esto nos da la velocidad
y
Efectuando el producto escalar entre los vectores r y v obtenemos:
Con lo cual resulta que los vectores r y v son perpendiculares. Para la aceleración tenemos que
y así
La aceleración esta dirigida hacia O (aceleracion centripeta), y su modulo es constante.
Movimiento circular uniformemente acelerado
Aqui la aceleración angular α es constante y también ω(0) = 0
También, cuando φ(0)=0, así para el angulo de rotación
Así tenemos también que
y
o
Así, podemos deducir que la componente radial de la aceleracion (y su dirección) es
y su componente tangencial es
La velocidad angular como medida de direccion
A veces es muy útil ver a la velocidad angular como medida de la direccion y representarlo a través de un en el eje de
Ecuaciones de Movimiento en un sistema de coordenadas polares
Velocidad en coordenadas Polares
La velocidad v de una partícula material puede descomponerse en distintos tipos de componentes. Es usual e importante que se descomponga en componentes que tengan la dirección de los ejes de coordenadas, así se obtiene en la forma siguiente:
Otra alternativa puede ahora ser representado en un eje XY
Sistema de coordenadas
Un sistema de coordenadas es un conjunto de valores que permiten definir inequívocamente la posición de cualquier punto de un espacio euclídeo (o más generalmente variedad diferenciable). En física clásica se usan normalmente sistemas de coordenadas ortogonales, caracterizados por un punto denominado origen y un conjunto de ejes perpendiculares que constituyen lo que se denomina sistema de referencia Podemos llamarla bidimensional.
también, todo lo que presenta movimiento se puede medir bajo un sistema de referencia.
Sistemas usuales
Sistema de coordenadas cartesianas
El sistema de coordenadas cartesianas es aquel que formado por dos ejes en el plano, tres en el espacio, mutuamente perpendiculares que se cortan en el origen. En el plano, las coordenadas cartesianas o rectangulares x e y se denominan respectivamente abscisa y ordenada.
Sistema de coordenadas polares
Las coordenadas polares se definen por un eje que pasa por el origen (llamado eje ecopolar). La primera coordenada es la distancia entre el origen y el punto considerado, mientras que la segunda es el ángulo que forman el eje polar y la recta que pasa por ambos puntos.
Sistema de coordenadas cilíndricas
El sistema de coordenadas cilíndricas es una generalización del sistema de coordenadas polares plano, al que se añade un tercer eje de referencia perpendicular a los otros dos. La primera coordenada es la distancia existente entre el origen y el punto, la segunda es el ángulo que forman el eje y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada que determina la altura del cilindro.
Sistema de coordenadas esféricas
El sistema de coordenadas esféricas está formado por tres ejes mutuamente perpendiculares que se cortan en el origen. La primera coordenada es la distancia entre el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar la posición del punto.
Movimiento rectilíneo uniforme
Un movimiento es rectilíneo cuando describe una trayectoria recta y uniforme cuando su velocidad es constante en el tiempo, es decir, su aceleración es nula. Esto implica que la velocidad media entre dos instantes cualesquiera siempre tendrá el mismo valor. Además la velocidad instantánea y media de este movimiento coincidirán.
Ecuaciones del movimiento
Sabemos que la velocidad es constante.
Cálculo del espacio recorrido
Sabiendo que la velocidad es constante y según la definición de velocidad:
tenemos:
despejando términos:
integrando:
realizando la integral:
Donde es la constante de integración, que corresponde a la posición del móvil para , si en el instante , el móvil está en el origen de coordenadas, entonces . Esta ecuación determina la posición de la partícula en movimiento en función del tiempo.
Cálculo de la aceleración
Según la ecuación del movimiento y la definición de aceleración tenemos:
esto es:
sabiendo que la velocidad no varía con el tiempo, tenemos:
La aceleración es nula, como ya se sabía.
El reposo
Se debe notar que el reposo es un caso de movimiento rectilíneo uniforme en el que
Referencias
Dinámica
Dinámica es una rama de la física que estudia la relación entre las fuerzas que actúan sobre un cuerpo y los efectos que se producirán sobre el movimiento de los cuerpos.
La dinámica en el ámbito de la física está regulada por las Leyes de Newton lo cual obedece a 3 leyes: la primera ley, indica que un cuerpo se mantendrá en reposo o movimiento uniforme excepto que sobre el cuerpo actúe una fuerza; la segunda ley, establece que la variación del movimiento de los cuerpos es proporcional a la fuerza que se ejerce sobre él; la tercera ley expresa que a la fuerza que se aplica sobre un cuerpo se le opone una fuerza de la misma intensidad pero en dirección opuesta.
Leyes de Newton
Sin lugar a dudas, Newton fue uno de los matemáticos más sobresalientes en la historia de la humanidad. Su principal legado son las llamadas "Leyes de Newton", las cuales dan una explicación muy distinta a lo que normalmente conocemos como sólo movimiento. Estas leyes fueron los primeros modelos fisicos propuestos por el hombre para explicar el movimiento.
La segunda Ley de Newton establece la relación entre la fuerza y el movimiento, en ella se establece que "si sobre un cuerpo de masa m se aplica una fuerza F, este cuerpo adquiere una aceleración a que es directamente proporcional a la fuerza aplicada". Esta Ley se sintetiza en la siguiente fórmula:
Se denomina Leyes de Newton a tres leyes concernientes al movimiento de los cuerpos. La formulación matemática fue publicada por Isaac Newton en 1687, en su obra Philosophiae Naturalis Principia Mathematica. Las leyes de Newton constituyen, junto con la transformación de Galileo, la base de la mecánica clásica. En el tercer volumen de los Principia Newton mostró que, combinando estas leyes con su Ley de la gravitación universal, se pueden deducir y explicar las Leyes de Kepler sobre el movimiento planetario.
Debe aclararse que las leyes de Newton tal como comúnmente se exponen, sólo valen para sistemas de referencia inerciales. En sistemas de referencia no-inerciales junto con las fuerzas reales deben incluirse las llamadas fuerzas ficticias o fuerzas de inercia que añaden términos suplementarios capaces de explicar el movimiento de un sistema cerrado de partículas clásicas que interactúan entre sí.
Primera ley de Newton o Ley de Inercia
En ocasiones, esta ley se nombra también Principio de Galileo.
- En la ausencia de fuerzas, todo cuerpo continúa en su estado de reposo o de movimiento rectilíneo y uniforme respecto de un sistema de referencia Galileano.
Este principio puede ser reformulado de la manera siguiente:
- Un sistema de referencia en el que son válidas las leyes de la física clásica es aquel en el cual todo cuerpo permanece en un estado de movimiento rectilíneo y uniforme en ausencia de fuerzas.
La Primera ley constituye una definición de la fuerza como causa de las variaciones de velocidad de los cuerpos e introduce en física el concepto de sistemas de referencia inerciales o sistemas de referencia Galileanos. Los sistemas no inerciales son todos aquellos sistemas de referencia que se encuentran acelerados.
Esta observación de la realidad cotidiana conlleva la construcción de los conceptos de fuerza, velocidad y estado. El estado de un cuerpo queda entonces definido como su característica de movimiento, es decir, su posición y velocidad que, como magnitud vectorial, incluye la rapidez, la dirección y el sentido de su movimiento. La fuerza queda definida como la acción mediante la cual se cambia el estado de un cuerpo.
En la experiencia diaria, los cuerpos están sometidos a la acción de fuerzas de fricción o rozamiento que los van frenando progresivamente. La no comprensión de este fenómeno hizo que, desde la época de Aristóteles y hasta la formulación de este principio por Galileo y Newton, se pensara que el estado natural de movimiento de los cuerpos era nulo y que las fuerzas eran necesarias para mantenerlos en movimiento. Sin embargo, Newton y Galileo mostraron que los cuerpos se mueven a velocidad constante y en línea recta si no hay fuerzas que actúen sobre ellos. Este principio constituyó uno de los descubrimientos más importantes de la física.
Segunda Ley de Newton o Ley de la Fuerza
- La variación del momento lineal de un cuerpo es proporcional a la resultante total de las fuerzas actuando sobre dicho cuerpo y se produce en la dirección en que actúan las fuerzas.
Newton definió el momento lineal (momentum) o cantidad de movimiento como una magnitud representativa de la resistencia de los cuerpos a alterar su estado de movimiento definiendo matemáticamente el concepto coloquial de inercia.
- ,
donde m se denomina masa inercial. La segunda ley se escribe por lo tanto:
Esta ecuación es válida en el marco de la teoría de la relatividad de Albert Einstein si se considera que el momento de un cuerpo se define como:
Substituyendo en la ecuación de la fueza, la definción de la cantidad de movimiento clásica la segunda ley de Newton adquiere la forma más familiar de:
- .
Esta ley constituye la definición operacional del concepto de fuerza, ya que tan sólo la aceleración puede medirse directamente. De una forma más simple, se podría también decir lo siguiente:
- La fuerza que actúa sobre un cuerpo es directamente proporcional al producto de su masa y su aceleración.
Donde F es la fuerza aplicada, m es la masa del cuerpo y a la aceleración.
Tercera Ley de Newton o Ley de acción y reacción
- Por cada fuerza que actúa sobre un cuerpo, éste realiza una fuerza igual pero de sentido opuesto sobre el cuerpo que la produjo. Dicho de otra forma: Las fuerzas siempre se presentan en pares de igual magnitud y sentido opuesto.
Esta ley, junto con las anteriores, permite enunciar los principios de conservación del momento lineal y del momento angular.
Ley de acción y reacción fuerte
En la ley de acción y reacción fuerte, las fuerzas además de ser de la misma magnitud y opuestas, son colineales. La forma fuerte de la ley no se cumple siempre.
Ley de acción y reacción débil
En la ley de acción y reacción débil no se exige que las fuerzas de acción y reacción sean colineales, tan sólo de la misma magnitud y sentido opuesto, sin actuar necesariamente en la misma línea. Ciertos sistemas magnéticos no cumplen el enunciado fuerte de esta ley, y tampoco lo hacen las fuerzas eléctricas ejercidas entre una carga puntual y un dipolo. La forma débil de la ley de acción-reacción se cumple siempre. La cinemática de un punto se puede describir en un sistema de coordenadas cartesiano tridimensional con tres funciones que proporcionen la dependencia de cada una de ellas en función del tiempo.
En el caso del punto todas las fuerzas son concurrentes y se puede trabajar con la fuerza resultante , de la que se han de considerar sus tres componentes: , y . Derivando dos veces en función del tiempo y aplicando la segunda ley de Newton se encuentran las ecuaciones de la dinámica del punto.
Donde m es la masa del punto material.
Con estas ecuaciones se puede determinar completamente la cinemática de la masa puntual considerada.
Referencias
Discusión
Si se considera un sistema de puntos, la fuerza resultante sobre el punto i de todas las fuerzas, internas y externas, que actúan sobre el es:
donde es la resultante de todas las fuerzas internas del sistemas y la de todas las fuerzas externas.
Sumando para todas las particulas a considerar se obtiene un resultante para el sistema completo de partículas:
La ecuación anterior se puede simplificar dado que por el principio de acción y reacción sabemos que a toda fuerza interna sobre el punto i le ha de corresponder otra igual y de sentido opuesto ejercida en otro punto j, por lo que el primer sumatorio de la parte izquierda de la igualdad se anula, quedando solamente las fuerzas externas al sistema:
Si realizamos el ejercicio de considerar una masa puntal sometida a la misma fuerza que la resultante de fuerzas externas del sistema completo y con una masa igual a la masa total del sistema, podremos escribir:
donde vec{R} es el vector de posición del punto imaginario considerado y
Lo que inspira las siguientes definiciones.
Definición de centro de masas
El centro de masas de un sistema de puntos es el punto geométrico donde la resultante de las fuerzas ejercidas por todos los cuerpos del sistema se anula.
En un tratamiento de sistemas de masas puntuales el centro de masas es el punto donde se supone concentrada toda la masa del sistema. El concepto se utiliza para análisis físicos en los cuales no es importante considerar la distribución de masa. Por ejemplo, en las órbitas de los planetas.
Cálculo del CM de un sistema de masas discreto
Cálculo del CM de un sistema de masas continuo
Casos particulares en un sistema continuo
- Distribución de masa homogénea: Si la masa está distribuida homogéneamente, la densidad será constante por lo que se puede sacar fuera de la integral haciendo uso de la equivalencia
- Nota: V es el volumen total. Para cuerpos bidimensionales o monodimensionales se trabajará con densidades superficiales/longitudinales y con superficies/longitudes.
- - Para el caso de cuerpos con geometría regular tales como esferas, paralelepípedos, cilindros, etc. el CM coincidirá con el centro geométrico del cuerpo.
- Distribución de masa no homogénea: Los centros de masas en cuerpos de densidad variable pueden calcularse si se conoce la función de densidad . En este caso se calcula el CM de la siguiente forma.
- - La resolución de la integral dependerá de la función de la densidad.
Interpretación física del centro de masas
El centro de masa de un sistema es un punto que se comporta dinámicamente como si todas las fuerzas externas del sistema actuasen directamente sobre el.
Referencias
Rotación es el movimiento de cambio de orientación de un cuerpo extenso de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo. En un espacio tridimensional, para un movimiento de rotación dado, existe una línea de puntos fijos denominada eje de rotación.
La velocidad angular se expresa como el ángulo girado por unidad de tiempo y se mide en radianes por segundo. Otras unidades que se pueden utilizar son Hercios (ciclos por segundo) o revoluciones por minuto (rpm). Comúnmente se denomina por las letras: u . La rotación es una propiedad vectorial de un cuerpo. El vector representativo de la velocidad angular es paralelo a la dirección del eje de rotación y su sentido indica el sentido de la rotación siendo el sentido horario negativo y el sentido antihorario positivo. En ocasiones se utiliza también la frecuencia como medida escalar de la velocidad de rotación.
El grado de variación temporal de la frecuencia angular es la aceleración angular (rad/s²) para la cual se utiliza frecuentemente el símbolo .
Período y frecuencia: Estos parámetros son de uso frecuente en sistemas rotantes a velocidad constante. El período es el inverso de la frecuencia y representa el tiempo que se tarda en dar una revolución completa. Período y frecuencia se representan respectivamente como:
- Período:
- Frecuencia:
Transformaciones de rotación
En matemáticas las rotaciones son transformaciones lineales que conservan las normas en espacios vectoriales en los que se ha definido una operación de producto interior. La matriz de transformación tiene la propiedad de ser una matriz unitaria, es decir, es ortogonal y su determinante es 1.
Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes:
La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector) .
En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente:
.
Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo en sentido horario: , es decir
donde y son las componentes del nuevo vector después de ser rotado.
Teorema de rotación de Euler
El teorema de rotación de Euler dice que cualquier rotación o conjunto de rotaciones sucesivas puede expresarse siempre como una rotación alrededor de una única dirección o eje de rotación principal. De este modo, toda rotación (o conjunto de rotaciones sucesivas) en el espacio tridimensional puede ser especificada a través del eje de rotación equivalente definido vectorialmente por tres parámetros y un cuarto parámetro representativo del ángulo rotado. Generalmente se denominan a estos cuatro parámetros grados de libertad de rotación.
Referencias
Rotación alrededor de un eje fijo es un caso especial del movimiento rotacional. La hipótesis del eje fijo excluye la posibilidad de un eje en movimiento, y no puede describir fenómenos como el “bamboleo”.
De acuerdo al teorema de la rotación de Euler, la rotación alrededor de más de un eje al mismo tiempo es imposible, así pues, si dos rotaciones son forzadas al mismo tiempo en diferente eje, aparecerá un nuevo eje de rotación.
Las siguientes fórmulas y conceptos son útiles para comprender más a fondo la rotación sobre un eje fijo.
Relación entre el movimiento de rotación y el lineal
El movimiento de rotación tiene una estrecha relación con el movimiento lineal.
El desplazamiento lineal es el producto del desplazamiento angular por el radio del círculo descrito por el movimiento.
- s=θR
La velocidad lineal es el producto de la velocidad angular por el radio del círculo descrito por el movimiento.
- v=ωR
La aceleración tangencial es el producto de la aceleración angular por el radio del círculo descrito por el movimiento.
- a=αR
Así mismo, tomando en cuenta lo anterior, las fórmulas de la cinemática mantienen esta misma relación.
Mientras que las fórmulas de la cinemática del movimiento lineal son:
Para la cinemática del movimiento rotacional utilizaremos las siguientes:
- ω_f ^2 = ω_o ^2 + 2αθ
- ω_f=ω_o+αt
- θ=ω_o t+1/2 αt^2
Desplazamiento angular θ
El desplazamiento angular de un objeto determina la cantidad de rotación del mismo y es descrito por la siguiente fórmula:
- ∆θ=θ_2-θ_1
El desplazamiento angular se mide en radianes (rad), aunque también se puede medir en revoluciones (rev). A continuación se presentan la comparación entre unidades.
- 1 rad = 57.3° 1 rev = 360° = 2π rad
Velocidad angular ω
La velocidad angular es el cambio del desplazamiento angular con respecto al tiempo, como se presenta en la siguiente fórmula:
- ω= ∆θ/∆t =(θ_2-θ_1)/(t_2-t_1 )
La velocidad angular, es siempre la misma sin importar la distancia que haya entre una partícula y el eje de rotación.
Las unidades en que se expresa comúnmente la velocidad angular es en radianes por segundo (rad/s), pero también puede expresarse en revoluciones por minuto (rpm o rev/min) y en revoluciones por segundo (rev/s).
Aceleración angular α
Al igual que en el movimiento lineal, el movimiento rotacional puede tener aceleración. La velocidad angular puede alterarse por la influencia de un momento de torsión resultante.
La fórmula para calcular la aceleración angular es la siguiente:
Momento de torsión (torque)
En la ley del movimiento rotacional, Newton menciona lo siguiente:
| Un momento de torsión resultante aplicado a un cuerpo rígido siempre genera una aceleración angular que es directamente proporcional al momento de torsión aplicado e inversamente proporcional al momento de inercia del cuerpo. [1] |
Energía cinética rotacional.
Tomando en cuenta que la energía cinética lineal está dada por la siguiente fórmula:
- K=1/2 mv^2
Y manteniendo la misma relación que ya se expresó más arriba, la energía cinética rotacional está dada por la fórmula:
- K=1/2 mω^2 R^2
Pero, si consideramos que un cuerpo está formado por diversas partículas de masas diferentes y localizadas a diferentes distancias del eje de rotación, la energía cinética total del cuerpo sería la sumatoria de las energías cinéticas de todas las partículas del cuerpo.
- K_T=∑▒〖1/2 mω^2 R^2 〗
Y tomando en cuenta que la velocidad angular es la misma para todas las partículas, la fórmula podríamos ordenarla de la siguiente manera:
- K_T=1/2 ω^2 (∑▒〖mR^2 〗)
Viendo que la cantidad en paréntesis no considera si la partícula está en movimiento o en reposo, definiremos a esa cantidad como momento de inercia.
Momento de inercia
La inercia es una propiedad de la materia para resistirse a cualquier cambio en su estado, ya sea de reposo o de movimiento como lo describe la Primera Ley de Newton:
| Un cuerpo permanece en estado de reposo o de movimiento rectilíneo uniforme, a menos que una fuerza externa no equilibrada actúe sobre él. Primera Ley de Newton[2]
|
Todos los cuerpos que giran alrededor de un eje desarrollan una inercia a la rotación (se resisten a cambiar su velocidad de rotación y la dirección de su giro. La inercia de un cuerpo a la rotación está determinada por su momento de inercia, que es la resistencia que opone un cuerpo en rotación al cambio de su velocidad de rotación.
La fórmula para calcular el momento de inercia de un cuerpo compuesto por partículas de masas dispersas es la siguiente:
- I=∑▒〖mR^2〗
Para calcular el momento de inercia de cuerpos con distribuciones parejas de masa, se utilizan fórmulas específicas para cada cuerpo. Algunos de los más comunes son los siguientes:
- Aro delgado:
- Aro delgado alrededor de uno de sus diámetros :
- Disco sólido:
- Cilindro sólido:
- Cilindro hueco:
- Barra delgada con eje a través de su centro :
- Barra delgada con eje en uno de sus extremos:
- Esfera sólida con eje en su diámetro:
- Esfera hueca de pared delgada:
Dada la fórmula del momento de inercia, podemos darnos cuenta de que la unidad en que se mide la inercia es en kilogramo-metro al cuadrado (kg m²).[3]
Referencias
- ↑ Tippens, Paul (2001). «11» (en español). FÍSICA CONCEPTOS Y APLICACIONES (sexta edición). McGraw-Hill. pp. 253.
- ↑ Tippens, Paul (2001). «4» (en español). FÍSICA CONCEPTOS Y APLICACIONES (sexta edición). McGraw-Hill. pp. 74.
- ↑ Tippens, Paul (2001). «11» (en español). FÍSICA CONCEPTOS Y APLICACIONES (sexta edición). McGraw-Hill. pp. 241-259.
Uno de los tipos de movimiento con los que nos encontramos son movimientos repetitivos en los que la posición del objeto que se se muevo vuelve a su posición original. La situación de estos tipos de movimiento que es más fácil de analizar es el que transcurre en un plano. Para estudiarlo es útil definir una serie de magnitudes angulares.
Definición de radián
Si consideramos un punto que describe algún tipo de movimiento rotatorio y tomamos el segmento que una un punto interior a la trayectoria y el punto móvil, nos daremos cuenta que dicho segmento barre un ángulo hasta que se repite la posición original y el ángulo recorrido es de 360º.
Si bien la medición del ángulo en grados sexagesimales es una posibilidad para el estudio de la cinemática de la rotación, resulta más conveniente otra unidad, conocida como radian. Para definirlo consideremos un segmento de longitud constante que barre la superficie de un círculo. Si llamamos a la longitud del arco de circunferencia correspondiente al ángulo barrido en un tiempo y la longitud del segmento considerado, el ángulo en radianes es . Para un círculo completo es la longitud de la circunferencia y por tanto el número de radianes de un círculo completo es .
Coordenadas angulares
La coordenada fundamental para el estudio de la cinemática de la rotación es el ángulo , de la que se derivan otras dos magnitudes: la velocidad angular y la acelaración angular.
Velocidad angular: El módulo de la velocidad angular se define como
su dirección es la perpendicular al plano del movimiento y el sentido el definido por la w:regla de la mano derecha.
Aceleración angular: De forma análoga a la aceleración lineal, se define la aceleración angular como
Relación entre magnitudes lineales y angulares
En el caso estudiado de un partícula que describe un movimiento circular se puede determinar la velocidad lineal como
siendo un vector unitario tangencial a la trayectoria circular. La descripción de dicho vector unitario y el vector unitario radial en coordenadas cartesianas es
siendo el ángulo entre el radio que describe el movimiento de la partícula y el eje X.
Las derivadas con respecto al tiempo de los vectores unitarios son
y
Referencias
- Gettys, W. Edward, Keller, Frederick J., Skove, Malcom J. (1995). Física Clásica y Moderna. 84-7615-635-9.
Rotación en sólidos rígidos
En general se utiliza un cuerpo sólido ideal no puntual e indeformable denominado sólido rígido como ejemplo básico para estudiar los movimientos de rotación de los cuerpos. La velocidad de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el cuerpo y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del cuerpo a alterar su movimiento de rotación.
Cinemática de la rotación de sólidos rígidos: Para analizar el comportamiento cinemático de un cuerpo rígido debemos partir de la idea de que un angulo θ define la posición instantánea de cualquier partícula contenida en el cuerpo rígido (CR); este angulo se mide desde un plano perpendicular al eje de rotación del CR.
Si la posición queda completamente definida por la coordenada angular θ, entonces la velocidad del CR se podrá expresar como:
Mientras que la aceleración quedaría definida por:
La energía cinética de rotación se escribe:
- .
La expresión del teorema del trabajo en movimientos de rotación se puede expresar así: la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado ().
- .
Definición de momento de inercia
El momento de inercia o inercia rotacional es una magnitud que da cuenta de cómo es la distribución de masas de un cuerpo o un sistema de partículas alrededor de uno de sus puntos. Este concepto, desempeña en el movimiento de rotación un papel análogo al de la masa inercial en el caso del movimiento rectilíneo y uniforme.
Dado un eje arbitrario, para un sistema de partículas se define como la suma de los productos entre las masas de las partículas que componen un sistema, y el cuadrado de la distancia r de cada partícula a al eje escogido. Representa la inercia de un cuerpo a rotar. Matemáticamente se expresa como:
Para un cuerpo de masa continua (Medio continuo) lo anterior se generaliza como:
El subíndice V de la integral indica que hay que integrar sobre todo el volumen del cuerpo.
Este concepto, desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme. Así, por ejemplo, la segunda ley de Newton: tiene como equivalente para la rotación:
donde:
- es el momento aplicado al cuerpo.
- es el momento de inercia del cuerpo con respecto al eje de rotación y
- es la aceleración angular.
La energía cinética de un cuerpo en movimiento con velocidad v es , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es . Donde I es el momento de inercia con respecto al eje de rotación.
La conservación de la cantidad de movimiento o momento lineal tiene por equivalente la conservación del momento angular :
El vector momento angular tiene la misma dirección que el vector velocidad angular .
Momentos de inercia de cuerpos simples

| Descripción | ||
|---|---|---|
| varilla respecto a un eje que pasa por su centro | ||
| anillo delgado respecto al eje | ||
| anillo delgado respecto a un diámetro | ||
| cilindro macizo respecto a su eje de revolución | ||
| esfera respecto a un diámetro |
Tensor de inercia de un sólido rígido
El tensor de inercia de un sólido rígido, es un tensor simétrico de segundo orden, que expresado en una base ortonormal viene dado por una matriz simétrica, dicho tensor se forma a partir de los momentos de inercia según tres ejes perpendiculares y tres productos de inercia tal como se explica a continuación.
Tal como se explica al principio del artículo, para un sólido rígido tridimensional pueden definirse momentos de inercia según diversos ejes, en particular pueden definirse según tres ejes perpendiculares prefijados indepedientes que llamaremos X, Y y Z:
Además de estas magnitudes pueden definirse los llamados productos de inercia:
Todas las formas anteriores pueden resumirse en la siguiente fórmula tensorial:
Donde y donde .
El momento con respecto a cualquier otro eje puede expresarse como combinación lineal anterior de las anteriores magnitudes:
Donde la matriz anterior es el tensor de inercia expresado en la base XYX y t = (tx, ty, tz) es el vector paralelo al eje según el cual se pretende encontrar el momento de inercia.
Derivación formal del tensor de inercia
La velocidad de un cuerpo rígido se puede escribir como la suma de la velocidad del centro de masa más la velocidad de un elemento del sólido, matemáticamente esto es
donde es la velocidad, es la velocidad del centro de masa, es la velocidad angular medida en un sistema solidario al sólido y es la distancia entre el orígen de este sistema y el elemento del sólido. Si se toma la norma al cuadrado de este vector se puede obtener la energía cinética de dicho diferencial de cuerpo rígido, a saber
donde , con la densidad del cuerpo y un elemento de volumen. Para obtener la energía cinética total del cuerpo rígido se debe integrar en todo el volumen de éste:
Con el fin de anular el último término, i. e. simplificar la expresión (y las sucesivas), se elige el origen del sistema solidario al sólido en el centro de masa. De este modo
pues, en virtud de la elección hecha . Se tiene luego que
es evidente, que el primer término el la energía cinética debido a la traslación del cuerpo. El otro término, en consecuencia, debe ser la energía asociada a la rotación del mismo. Si se escribe explícitamente el integrando de este último término se tiene
donde es claro que:
con la delta de Kronecker. Poniendo este resultado en la expresión asociada a la energía cinética debido a la rotación y poniendo la integral dentro de la sumatoria se tiene
Debe notarse que el factor correspondiente a la integral depende únicamente de las característica geométricas (físicas) del cuerpo. En efecto, depedende de su forma (volumen) y de la masa del cuerpo y de como cómo está distribuida en dicha forma. Este factor es la componente de un cierta matriz que se conoce como Tensor de Inercia, puesto que toda matriz corresponde a un tensor de segundo rango:
A los elementos se los llama momento de inercia respecto del eje . Claramente, se ve que el tensor de inercia es simétrico, por lo tanto es siempre diagonalizable. Es decir, siempre se puede encontrar una base de vectores tal que dicha matriz tenga forma diagonal. Tales vectores definen lo que se conoce como ejes principales. En otras palabras, siempre se puede elegir un sistema completo de vectores ortonormales (ejes principales) con los cuales el tensor de incercia toma forma diagonal.
Concepto de Momento Angular
El momento angular, en el contexto de las rotaciones, se refiere a la cantidad de movimiento rotacional que posee un objeto al girar alrededor de un eje. Este concepto es fundamental para comprender la conservación del momento angular, la estabilidad de sistemas giratorios y la transferencia de energía en sistemas rotacionales.
Aplicaciones en la Física
En el ámbito de la física, el momento angular es esencial para describir fenómenos como el movimiento de planetas, el giro de partículas subatómicas y la dinámica de sistemas rotativos. La comprensión del momento en las rotaciones permite explicar la conservación de la cantidad de movimiento en sistemas a escala microscópica y macroscópica.
Ingeniería y Tecnología
En ingeniería, el momento angular es crucial para el diseño y análisis de sistemas rotativos, como motores, turbinas y dispositivos mecánicos. La aplicación del momento angular en ingeniería permite optimizar la eficiencia y estabilidad de máquinas y mecanismos que operan mediante el movimiento rotacional.
Vida Cotidiana
En la vida cotidiana, el momento en las rotaciones se manifiesta en actividades que van desde el giro de ruedas en vehículos hasta el funcionamiento de dispositivos eléctricos y electrónicos. Comprender el momento angular es fundamental para el diseño y operación segura de tecnologías presentes en la vida diaria.
Conclusión
En resumen, el momento en las rotaciones es un concepto esencial en la descripción y comprensión de fenómenos físicos, ingenieriles y cotidianos que involucran movimiento rotacional. Su aplicación permite abordar la conservación de la cantidad de movimiento en sistemas giratorios, lo que tiene implicaciones significativas en el desarrollo de tecnologías y la comprensión de la naturaleza. El momento angular o momento cinético de una masa puntual, es igual al producto vectorial del vector de posición (brazo), del objeto en relación a la recta considerada como eje de rotación, por la cantidad de movimiento (también llamado momento lineal o momento). Frecuentemente se lo designa con el símbolo :
En ausencia de momentos de fuerzas externos, el momento angular de un conjunto de partículas, de objetos o de cuerpos rígidos se conserva. Esto es válido tanto para partículas subatómicas como para galaxias.
Momento angular de una masa puntual

En el dibujo de derecha vemos una masa que se desplaza con una velocidad instantánea . El momento angular de esta partícula, con respecto a la recta perpendicular al plano que contiene y es, como ya se ha escrito:
El vector es perpendicular al plano que contiene y , luego es paralelo a la recta considerada como eje de rotación. En el caso del dibujo, el vector momento angular sale del dibujo y va hacia el observador.
El módulo del momento angular es:
Es decir, el módulo es igual al momento lineal multiplicado por su brazo, el cual es la distancia entre el eje de rotación y la recta que contiene la velocidad de la partícula. Por esta razón, algunos designan el momento angular como el "momento del momento".
Dependencia temporal
Derivemos el momento angular con respecto al tiempo:
El primero de los paréntesis es cero ya que la derivada de con respecto al tiempo no es otra cosa que la velocidad . Y como el vector velocidad de paralelo al vector cantidad de movimiento , el producto vectorial de los dos es cero. Nos queda el segundo paréntesis:
donde es la aceleración. Pero , la fuerza aplicada a la masa. Y el producto vectorial de por la fuerza es el torque o momento de fuerza aplicado a la masa:
La derivada temporal del momento angular es igual al torque aplicado a la masa puntual.
Momento angular de un conjunto de partículas
El momento angular de un conjunto de partículas es la suma de los momentos angulares de cada una:
La variación temporal es:
El término de derecha es la suma de todos los torques producidos por todas las fuerzas que actúan sobre las partículas. Una parte de esas fuerzas puede ser de origen externo al conjunto de partículas. Otra parte puede ser fuerzas entre partículas. Pero cada fuerza entre partículas tiene su reacción que es igual pero de dirección opuesta y colineal. Eso quiere decir que los torques producidos por cada una de las fuerzas de un par acción-reacción son iguales y de signo contrario y que su suma se anula. Es decir, la suma de todos los torques de origen interno es cero y no puede hacer cambiar el valor del momento angular del conjunto. Solo quedan los torques externos:
El momento angular de un conjunto de partículas se conserva en ausencia de torques externos.
Esta afirmación es válida para cualquier conjunto de partículas: desde núcleos atómicos hasta grupos de galaxias.
Cuerpos rígidos
Cuando el conjunto de partículas forma un cuerpo rígido, sabemos que
donde:
- es el torque aplicado al cuerpo.
- es el momento de inercia del cuerpo.
- es la aceleración angular del cuerpo.
Luego:
Como el momento angular es cero si no hay rotación:
donde es la velocidad angular del cuerpo.
Teorema de Steiner
El teorema de Steiner establece que el momento de inercia con respecto a cualquier eje paralelo a un eje que pasa por el centro de gravedad, es igual al momento de inercia con respecto al eje que pasa por el centro de gravedad de un cuerpo, más el producto de la masa por el cuadrado de la distancia entre los dos ejes:
Donde: Ieje es el momento de inercia respecto al eje que no pasa por el centro de masa; I(CM)eje es el momento de inercia para un eje paralelo al anterior que pasa por el centro de gravedad; M - Masa de la sección transversal y h - Distancia entre los dos ejes paralelos considerados. La demostración de este teorema resulta inmediata si consideramos la descomposición de coordenadas relativa al centro de masas C inmediata:
Donde el segundo término es nulo puesto que la distancia vectorial promedio de masa en torno al centro de masa es nula, por la propia definición de centro de masa.
Aplicación de la Dinámica a la Rotación
La Dinámica de la Rotación se aplica en situaciones donde un objeto gira alrededor de un eje fijo, como una rueda girando, una peonza o un planeta orbitando alrededor de una estrella. Algunas de las aplicaciones de la dinámica a la rotación incluyen:
- Momento de Inercia: El momento de inercia se utiliza para calcular la resistencia de un objeto a cambiar su velocidad angular. Este concepto es fundamental para comprender cómo se comportan los objetos en rotación.
- Torque y Energía Rotacional: El torque es la medida de la tendencia de una fuerza a hacer girar un objeto alrededor de un eje, mientras que la energía rotacional se relaciona con la capacidad de un objeto en rotación para realizar trabajo.
- Conservación del Momento Angular: Al igual que la conservación del momentum lineal, la conservación del momento angular es una ley fundamental en la física, y se aplica a sistemas en rotación.
Estas aplicaciones ayudan a comprender el comportamiento de los objetos en rotación y son fundamentales en campos como la ingeniería, la física y la astronomía.
Magnitudes mecánicas fundamentales
SISTEMA INTERNACIONAL.
MAGNITUDES FUNDAMENTALES.
Midiendo la distancia recorrida por un coche y el tiempo que ha estado caminando podemos determinar su velocidad. Como la velocidad se calcula a partir de la distancia y el tiempo, decimos que son magnitudes fundamentales y que la velocidad es derivada.
Pero se trata de algo arbitrario, porque podríamos medir la velocidad del coche y el tiempo que estuvo andando para, a partir de ahí, calcular la distancia recorrida. Entonces velocidad y tiempo serían magnitudes fundamentales y la distancia una magnitud derivada.
Para eludir estos problemas de interpretación, los científicos del mundo se han puesto de acuerdo en determinar qué magnitudes son fundamentales, cuáles son derivadas y en qué unidades deben medirse. Esto (magnitudes y unidades) se conoce como Sistema Internacional. Las magnitudes fundamentales del sistema internacional son:
- Longitud: Se mide en metros (m). El metro se define como la longitud recorrida por la luz en el vacío en un intervalo de tiempo de 1/299792458 de segundo.
- Masa: Se mide en kilogramos (kg). El kilogramo se define como la masa de un cilindro que se conserva en Paris. INTRODUCCIÓN AL MÉTODO CIENTÍFICO 3º E.S.O. 32 PROYECTO ANTONIO DE ULLOA
- Tiempo: Se mide en segundos (s). El segundo se define como la duración de 9192631770 periodos de la radiación correspondiente a la transición entre los dos niveles energéticos hiperfinos del estado fundamental del átomo de cesio-133.
Referencias
Energía
La energía es una magnitud física abstracta, ligada al estado dinámico de un sistema cerrado y que permanece invariable con el tiempo. Todos los cuerpos, por el sólo hecho de estar formados de materia, contienen energía, además, pueden poseer energía adicional debido a su movimiento, a su composición química, a su posición, a su temperatura y a algunas otra propiedades. Por ejemplo se puede decir que un sistema con energía cinética nula está en reposo. La variación de energía de un sistema es igual en magnitud al trabajo requerido para llevar al sistema desde un estado inicial al estado actual. El estado inicial es totalmente arbitrario.
La energía no es un ente físico real, ni una "substancia intangible" sino sólo un número escalar que se le asigna al estado del sistema físico, es decir, la energía es una herramienta o abstracción matemática de una propiedad de los sistemas físicos.
El uso de la magnitud energía en términos prácticos se justifica porque es mucho más fácil trabajar con magnitudes escalares, como lo es la energía, que con magnitudes vectoriales como la velocidad y la posición. Así, se puede describir completamente la dinámica de un sistema en función de las energías cinética, potencial y de otros tipos de sus componentes. En sistemas aislados además la energía total tiene la propiedad de conservarse es decir ser invariante en el tiempo. Matemáticamente la conservación de la energía para un sistema es una consecuencia directa de que las ecuaciones de evolución de ese sistema sean independientes del instante de tiempo considerado, de acuerdo con el teorema de Noether.
Energía potencial
Si en una región del espacio existe un campo de fuerzas conservativo, entonces el trabajo requerido para mover una masa cualquiera desde un punto de referencia, usualmente llamado nivel de tierra y otro es la energía potencial del campo. Por definición el nivel de tierra tiene energía potencial nula.
Energía cinética de una masa puntual
Es igual en magnitud al trabajo requerido para llevar la partícula al estado en el que se encuentra.
Dado que los cuerpos están formados de partículas, se puede conocer su energía sumando las energías individuales de cada partícula.
Energía en diversos tipos de sistemas
Todos los cuerpos, pueden poseer energía debido a su movimiento, a su composición química, a su posición, a su temperatura, a su masa y a algunas otras propiedades. En las diversas disciplinas de la física y la ciencia, se dan varias definiciones de energía, por supuesto todas coherentes y complemetarias entre sí, todas ellas siempre relacionadas con el concepto de trabajo.
Referencias
Trabajo, potencia
En mecánica, el trabajo efectuado por una fuerza aplicada sobre una partícula durante un cierto desplazamiento se define como el producto , dependiente de la trayectoria y, por lo tanto, no constituye una variable de estado. La unidad básica de trabajo en el Sistema Internacional es Newtonxmetro y se denomina Julio.
Fórmulas

En trayectorias lineales se expresa como:
siendo
- es el vector resultante de todas las fuerzas aplicadas, que para el caso deben tener la misma dirección que el vector desplazamiento pero no necesariamente el mismo sentido. Si los vectores tienen dirección opuesta, es decir quedan como rectas secantes formando un ángulo recto el trabajo efectuado es 0.
- es el vector desplazamiento
donde indica la componente tangencial de la fuerza a la trayectoria.
Para calcular el trabajo a lo largo de toda la trayectoria basta con integrar entre los puntos inicial y final de la curva. En el caso más simple de una fuerza constante aplicada sobre una distancia , el trabajo realizado se expresa como la formula siguiente:
Relación entre trabajo y energía
También se llama trabajo a la energía usada para deformar un cuerpo o, en general, alterar la energía de cualquier sistema físico. El concepto de trabajo está ligado íntimamente al concepto de energía y ambas magnitudes se miden en la misma unidad, el julio.
Esta ligazón puede verse en el hecho que, del mismo modo que existen distintas definiciones de energía para la mecánica y la termodinámica, también existen distintas definiciones de trabajo en cada rama de la física. Es una magnitud de gran importancia para establecer nexos entre las distintas ramas de la física.
Trabajo y energía son conceptos que empezaron a utilizarse cuando se abordó el estudio del movimiento de los cuerpos.
Potencia
En Física, potencia es la cantidad de trabajo efectuado por unidad de tiempo. Esto es equivalente a la velocidad de cambio de energía en un sistema o al tiempo empleado en realizar un trabajo, según queda definido por:
- ,
donde
- P es la potencia
- E es la energía o trabajo
- t es el tiempo.
La potencia se puede considerar en función de la intensidad y la superficie:
P = I · S
- P es la potencia realizada
- I es la intensidad
- S es la superficie
La unidad de potencia en el Sistema internacional (SI) es el vatio (W), el cual es equivalente a un julio por segundo.
Fuera del SI también se utiliza el caballo de vapor (CV), equivalente a la potencia necesaria para elevar verticalmente un peso de 75 kgf a una velocidad constante de 1 m/s (movimiento uniforme). Teniendo en cuenta que un kilopondio o kilogramo-fuerza (kg-f) es la fuerza ejercida sobre una masa de 1 kg por la gravedad estándar en la superficie terrestre, esto es, 9,80665 m/s2, entonces
Referencias
Campos y energía potencial
Concepto de campo
El concepto de campo en física se refiere a una magnitud que presenta cierta variación sobre una región del espacio. En ocasiones campo se refiere a una abstracción matemática para estudiar la variación de una cierta magnitud física; en este sentido el campo puede ser un ente no visible pero sí medible. Históricamente fue introducido para explicar la acción a distancia de las fuerzas de gravedad, eléctrica y magnética, aunque con el tiempo su significado se ha extendido substancialmente.
En física el concepto surge ante la necesidad de explicar la forma de interacción entre cuerpos en ausencia de contacto físico y sin medios de sustentación para las posibles interacciones.
La acción a distancia se explica, entonces, mediante efectos provocados por la entidad causante de la interacción, sobre el espacio mismo que la rodea, permitiendo asignar a dicho espacio propiedades medibles. Así, será posible hacer corresponder a cada punto del espacio valores que dependerán de la magnitud del cuerpo que provoca la interacción y de la ubicación del punto que se considera.
Campos clásicos de fuerzas
Los campos más conocidos en física clásica son:
- Campo electromagnético, superposición de los campos:
- campo electrostático.
- campo magnético.
- Campo gravitatorio.
- Accion a Distancia.
- Fuerzas de contacto.
- Fuerza Nuclear Fuerte
- Fuerza Nuclear Debil
Clasificación por tipo de magnitud
Una clasificación posible atendiendo a la forma matemática de los campos es:
- Campo escalar: aquel en el que cada punto del espacio lleva asociada una magnitud escalar. (campo de temperaturas de un sólido, campo de presiones atmosféricas...)
- Campo vectorial: aquel en que cada punto del espacio lleva asociado una magnitud vectorial (campos de fuerzas,...).
- Campo tensorial: aquel en que cada punto del espacio lleva asociado un tensor (campo electromagnético en electrodinámica clásica, campo gravitatorio en teoría de la relatividad general, campo de tensiones de un sólido, etc.)
Energía potencial
La energía potencial puede pensarse como la energía almacenada en un sistema, o como una medida del trabajo que un sistema puede entregar. Más rigurosamente, la energía potencial es una magnitud escalar asociado a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energia potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A. Posee un cuerpo en función de la posición que ocupa
Energía potencial asociada a campos de fuerzas
La energía potencial puede definirse solamente cuando la fuerza es conservativa, es decir que cumpla con alguna de las siguientes propiedades:
- El trabajo realizado por la fuerza entre dos puntos es independiente del camino recorrido.
- El trabajo realizado por la fuerza para cualquier camino cerrado es nulo.
- Cuando el rotor de F es cero.
Se puede demostrar que todas las propiedades son equivalentes (es decir que cualquiera de ellas implica la otra). En estas condiciones, la energía potencial se define como
De la definición se sigue que si la energía potencial es conocida, se puede obtener la fuerza a partir del gradiente de U:
También puede recorrerse el camino inverso: suponer la existencia una función energía potencial y definir la fuerza correspondiente mediante la fórmula anterior. Se puede demostrar que toda fuerza así definida es conservativa.
Evidentemente la forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico) el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.
Energía potencial gravitatoria
- Caso general. La energía potencial gravitatoria VG de una partícula material de masa m situada dentro del campo gravitatorio terrestre viene dada por:
Donde:
, distancia entre la partícula material del centro de la Tierra.
, constante universal del la gravitación.
, masa de la tierra.
Esta última es la fórmula que necesitamos emplear, por ejemplo, para estudiar el movimiento de satélites y misiles intercontinentales
- Cálculo simplificado. Cuando la distancia recorrida por un móvil h es pequeña, lo que sucede en la mayoría de las aplicaciones usuales (tiro parabólico, saltos de agua, etc.), podemos usar el desarrollo de Taylor a la anterior ecuación. Así si llamamos r a la distancia al centro de la tierra, R al radio de la Tierra y h a la altura sobre la superficie de la Tierra tenemos:
Donde hemos introducido la aceleración sobre la superfice:
Por tanto la variación de la energía potencial gravitatoria al desplazarse un cuerpo de masa m desde una altura h1 hasta una altura h2 es:
Dado que la energía potencial se anula cuando la distancia es infinita, frecuentemente se asigna energía potencial cero a la altura correspondiente a la del suelo, ya que lo que es de interés no es el valor absoluto de V, sino su variación durante el movimiento.
Así, si la altura del suelo es h1 = 0, entonces la energía potencial a una altura h2 = h será simplemente VG = mgh.
Energía potencial electrostática
La energía potencial electrostática de un sistema formado por dos partículas de cargas q y Q situadas a una distancia r una de la otra es igual a:
- llamada la Ley_de_Coulomb
Siendo K una constante universal o contante de Coulomb cuyo valor aproximado es 9*109 (voltios·metro/culombio).
La constante es la Constante de Coulomb y su valor para unidades SI es Nm²/C² (Voltio equivale a Newton/m).
Y siendo la constante de permisibilidad eléctrica en el vacio F/m.
Energía potencial elástica
- Potencial armónico (caso unidimensional).
- Dado una partícula en un campo de fuerzas que responda a la ley de Hooke (F= -k|r|) siendo k la constante de dicho campo, su energía potencial será V = 1/2 K |r|².
- Energía de deformación (caso general)
- En este caso la función escalar que da el campo de tensiones es la energía libre de Helmholtz por unidad de volumen f que representa la energía de deformación. En función de las deformaciones εij:
Donde la conexión con las tensiores viene dada por las siguientes relaciones termodinámicas:
Referencias
Impulso
En mecánica clásica, un impulso cambia el momento lineal de un objeto, y tiene las mismas unidades y dimensiones que el momento lineal. Las unidades del impulso en el Sistema Internacional son kg·m/s. Un impulso se calcula como la integral de la fuerza con respecto al tiempo.
donde
- I es el impulso, medido en kg·m/s
- F es la fuerza, medida en newtons
- t es la duración del tiempo, medida en segundos
En presencia de una fuerza constante el impulso se suele escribir con la fórmula:
donde
- es el intervalo de tiempo en el que se aplica la fuerza (F).
Usando la definición de campos de fuerza:
Así pues, lo más común es definir el impulso como una variación de cantidad de movimiento.
Teorema del momento cinético
Física/Magnitudes mecánicas fundamentales/Teorema del momento cinético
Principios de conservación
Uno de los objetivos de la mecánica es la prediccion del movimiento de los cuerpos materiales, para lo que se requiere saber que información del pasado es la más relevante a la hora pronosticar el futuro. Los principios de conservación que tratan sobre magnitudes que no varian en el tiempo bajo ciertas condiciones son muy útiles en la predicción ya que conociendo su magnitud en un momento dado conocemos automáticamente su valor otros tiempos.
Principio de conservación de la cantidad de movimiento
En un sistema aislado en el cual las fuerzas externas son cero, el momento lineal total se conserva. Al sistema o conjunto de partículas, que cumple esta ley se le llama Sistema inercial:
Por la Segunda Ley de Newton, tenemos:
Pero como la aceleración es:
Entonces, la fuerza la podemos escribir como:
Como las fuerzas externas son 0:
Dado que la derivada de una constante es 0:
Sin utilizar cálculo diferencial
La Segunda Ley de Newton puede ser planteada en términos de cantidad de movimiento:
De la segunda Ley de Newton obtenemos que:
Como la aceleración es:
Reemplazando con la aceleración:
Reemplazando con la cantidad de movimiento:
Si:
Entonces la cantidad de movimiento final será igual al inicial. A esto se le conoce como conservación de momento.
Equivalencia con leyes de Newton
Primera Ley o Inercia
Si la masa es constante esto implica que
Esto es equivalente a la primera ley de Newton o ley de la inercia, que establece que "en ausencia de fuerzas aplicadas un cuerpo se moverá con velocidad constante".
Segunda Ley
La segunda ley de Newton explica que al aplicar una fuerza externa a un cuerpo éste se acelerará, siendo esta fuerza igual al producto de la masa por la aceleración, es decir
De acuerdo a la definición de aceleración esta expresión también puede escribirse como
Si la masa es constante esto es equivalente a
lo que puede considerarse como una definición de fuerza: "fuerza es la razón de cambio del momento con respecto al tiempo".
Hay que resaltar que cuando Newton describió su Segunda Ley, en la que se describe qué es una fuerza, lo hizo derivando el momento lineal. Llegó a la conclusión de que para variar el momento lineal de una partícula, habría que aplicarle una fuerza. Por tanto la definición correcta de Fuerza es . Y, sólo en el muy probable caso de que la masa permanezca constante en dt, se puede transformar en . Lo normal es que al aplicarle una fuerza a un cuerpo, su masa permanezca constante; pero por ejemplo, en el caso de un cohete, esto no es así, pues va perdiendo masa según avanza.
Tercera Ley o Acción-Reacción
Finalmente, en la interacción entre dos cuerpos, si el momento ha de conservarse el cambio de momento de uno de los cuerpos debe ser el negativo del cambio de momento del otro
lo que de acuerdo a la definición de fuerza, puede expresarse como
que equivale al enunciado "a toda fuerza de acción le corresponde una fuerza de reacción igual y opuesta".
Principio de conservación de la energía
Física/Magnitudes mecánicas fundamentales/Principio de conservación de la energía
Principio de conservación del momento cinético
Física/Magnitudes mecánicas fundamentales/Principio de conservación del momento cinético
Descomposición de la energía cinética
La energía cinética de un solido rígido se expresa como la suma de dos componentes de ésta:
Energía cinética de traslación
Sea un cuerpo de masa , cuyo centro de masa se mueve con una velocidad . Su energía cinética de traslación es aquella que posee este cuerpo por el mero hecho de encontrarse su centro de masas en movimiento. Ésta viene dada por la expresión:
Energía cinética de rotación
Sea Un cuerpo de momento de inercia (o inercia rotacional) , el cual se mueve respecto a su centro de masa con una velocidad angular (que será la misma en cualquier punto del cuerpo que consideramos ya que se trata de un cuerpo rígido no deformable). Su energía cinética de rotación es aquella que posee este cuerpo por el mero hecho de encontrarse en movimiento circular respecto a su propio centro de masas. Ésta viene dada por la expresión:
Energía cinética total
Así, como hemos visto, un cuerpo no solo posee energía cinética por su velocidad lineal de traslación, si no que también posee energía debido a su movimiento de rotacion con respecto a su centro de masas. Por lo tanto, su energía cinética total será la suma algebraica de ambas ya que el movimiento de un sólido rígido siempre se puede descomponer en un movimiento de traslación de su centro de masas y otro de rotacion del cuerpo con respecto al centro de masas:
Campo gravitatorio
- Introducción al Campo gravitatorio
- Energía potencial en un campo gravitatorio
- Leyes de Kepler
- Centro de gravedad
Energía potencial en un campo gravitatorio
Ley de la Gravitación Universal de Newton
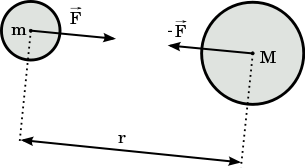
La Ley de la Gravitación Universal de Newton establece que la fuerza que ejerce una partícula puntual con masa sobre otra con masa es directamente proporcional al producto de las masas, e inversamente proporcional al cuadrado de la distancia que las separa:
donde es el vector unitario que va de la partícula 1 a la 2, y donde es la Constante de gravitación universal, siendo su valor 6,67 × 10–11 Nm2/kg2.
Trabajo realizado por la gravedad
De la definición de trabajo se puede calcular el trabajo ejercido por la fuerza gravitatoria de atracción de dos masas. Para ello realizaremos la integral a lo largo de la línea que une los centros de ambas masas
La Gravedad como fuerza conservativa
Se entiende que una fuerza es conservativa cuando el trabajo realizado por la misma entre dos puntos cualesquiera, no depende de la trayectoria seguida.
Para que una fuerza sea conservativa ha de poder escribirse como el gradiente de un escalar. Para demostralo supongamos que sea posible, entonces
Si para obtener el trabajo a lo largo de una trayectoria cualquiera integramos la expresión anterior obtenemos
es decir el resultado depende unicamente de la posición inicial y final y por tanto es conservativa.
Para la gravedad si recordamos el resultado para una trayectoria particular podremos ver una posible forma el potencial de la fuerza gravitatoria
si calculamos el gradiente recuperamos la ley de la gravitación de Newton
La forma más fácil de calcular el gradiente anterior es hacerlo en coordenada cilíndricas
Aplicandolo al inverso de r obtenemos
con lo que se recupera la expresión de la fuerza gravitatoria de partida
Leyes de Kepler
Johannes Kepler basó sus leyes en los primero estudios de Copérnico, quien fórmulo el modeo heliocentrico. La diferencia fue que Kepler, concluye que las órbitas de los planetas son elípticas con el Sol en uno de sus focos.
Las tres leyes de Kepler:
1) "Los planetas describen órbitas elípticas entorno al Sol".
2) "La recta que une un planeta cualquiera con el Sol (radio vector) describe áreas iguales en tiempos iguales". Esta ley es más conocida como la "ley de las áreas"
3) "Los cuadrados de los períodos de revolución de los planetas son proporcionales a los cubos de sus distancias medias al Sol".
Datos para aplicar la 3 ley:
T en años, a en unidades astronómicas.
Mercurio: T = 0,241 a = 0,387 Venus: T = 0,616 a = 0,723 Tierra: T = 1 a = 1 Marte: T = 1,88 a = 1,524 Júpiter: T = 11,9 a = 5,203 Saturno: T = 29,5 a = 9,539 Urano: T = 84,0 a = 19,191 Neptuno: T = 165,0 a = 30,071
Centro de gravedad
El centro de gravedad (C.G.) Es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas masas materiales de un cuerpo.
En física, el entronice, el centro de gravedad y el centro de masas pueden, bajo ciertas circunstancias, coincidir entre sí. En éstos casos es válido utilizar estos términos de manera intercambiable (como sinonimos).
El centroide es un concepto puramente geométrico, mientras que los otros dos términos se relacionan con las propiedades físicas de un cuerpo. Para que el centroide coincida con el centro de masas, el objeto tiene que tener densidad uniforme, o la distribución de materia a través del objeto debe tener ciertas propiedades, tales como simetría.
Para que un centro de coincida con el centro de gravedad, el entronice debe coincidir con el centro de masas de un cuerpo u objeto, y éste debe estar bajo la influencia de un campo gravitatorio uniforme.
Estática
La Estática es la parte de la mecánica que estudia el equilibrio de fuerzas, sobre un cuerpo en reposo. La estática es la rama de la física que analiza los cuerpos en reposo: fuerza, par / momento y estudia el equilibrio de fuerzas en los sistemas físicos en equilibrio estático, es decir, en un estado en el que las posiciones relativas de los subsistemas no varían con el tiempo. La primera ley de Newton implica que la fuerza neta y el par neto (también conocido como momento de fuerza) de cada organismo en el sistema es igual a cero. De esta limitación pueden derivarse cantidades como la carga o la presión. La red de fuerzas de igual a cero se conoce como la primera condición de equilibrio, y el par neto igual a cero se conoce como la segunda condición de equilibrio. Un cuerpo esta en reposo cuando su velocidad es igual a cero y está en equilibrio cuando la aceleración es igual a cero.
Análisis del equilibrio mediante momentos
La estática proporciona, mediante el empleo de la mecánica del sólido rígido, solución a los problemas denominados isostáticos. En estos problemas, es suficiente plantear las condiciones básicas de equilibrio, que son:
- El resultado de la suma de fuerzas es nula.
- El resultado de la suma de momentos respecto a un punto es nulo.
- Estas dos condiciones, mediante el vector, se convierten en un sistema de ecuaciones, la resolución de este sistema de ecuaciones, es resolver la condición de equilibrio.
- Existen métodos de resolución de este tipo de problemas estáticos mediante gráficos, heredados de los tiempos en que la complejidad de la resolución de sistemas de ecuaciones se evitaba mediante la geometría, si bien actualmente se tiende al cálculo por ordenador.
Para la resolución de problemas (aquellos en los que el equilibrio se puede alcanzar con distintas combinaciones de esfuerzos) es necesario considerar ecuaciones de compatibilidad. Dichas ecuaciones adicionales de compatibilidad se obtienen mediante la introducción de deformaciones y tensiones internas asociadas a las deformaciones mediante los métodos de la mecánica de sólidos deformables, que es una ampliación de la teoría del sólido rígido que da cuenta de la deformabilidad de los sólidos y sus efectos internos.
Existen varios métodos clásicos basados la mecánica de sólidos deformables, como los teoremas de las fórmulas de Navier-Bresse, que permiten resolver un buen número de problemas de modo simple y elegante.
debemos tener en cuenta las formulas para torques : F=KX k es una constante.
Aplicaciones
La estática abarca el estudio del equilibrio tanto del conjunto como de sus partes constituyentes, incluyendo las porciones elementales de material.
Uno de los principales objetivos de la estática es la obtención de esfuerzos cortantes, fuerza normal, de torsión y momento flector a lo largo de una pieza, que puede ser desde una viga de un puente o los pilares de un rascacielos.
Su importancia reside en que una vez trazados los diagramas y obtenidas sus ecuaciones, se puede decidir el material con el que se construirá, las dimensiones que deberá tener, límites para un uso seguro, etc. mediante un análisis de materiales. Por tanto, resulta de aplicación en ingeniería estructural, ingeniería mecánica, construcción, siempre que se quiera construir una estructura fija. Para el análisis de una estructura en movimiento es necesario considerar la aceleración de las partes y las fuerzas resultantes.
El estudio de la Estática suele ser el primero dentro del área de la ingeniería mecánica, debido a que los procedimientos que se realizan suelen usarse a lo largo de los demás cursos de ingeniería mecánica.
Equilibrio y reposo
Física/Estática/Equilibrio y reposos
Equilibrio de un sólido rígido
Definición de sólido rígido

Un sólido rigido esta formado por un conjunto de masas puntuales cuyas posiciones relativas entre sí no varían en el tiempo. Matemáticamente:
Esto significa que un cuerpo rigido se mueve como un todo y su movimiento podrá descomponerse como un componente de desplazamiento del centro de masas y otro de rotación.
Condiciones de equilibrio
En el apartado de discusión del principio de conservación del momento angular se define el momento angular como:
para un sistema de partículas se tiene:
y derivando respecto al tiempo:
los sumandos del primer término se anulan por tratarse del producto vectorial de un vector consigo mismo, mientras que el segundo es la definición del torque o momento de la fuerza, definido como:
donde se han definido la fuerza externa sobre la partícula i como y la fuerza que ejerce la partícula j sobre la i como . Sustituyendo en la expresión del momento angular total se llega a la expresión:
El último término del segundo miembro de la ecuación anterior puede considerarse como una suma de pares de la siguiente forma:
donde se ha utilizado el principio de acción y reacción. Si se considera además el denominado principo de acción y reacción fuerte, que enuncia que las fuerzas entre dos partículas, además de ser iguales y opuestas, están sobre la recta que las une, el producto vectorial en el último término se anula y se tendrá que:
Lo que nos lleva a que las condiciones de equilibrio estatico de un sólido rígido requiere que la resultante de las fuerzas se anule y, además, que se anule la resultante de la suma de momentos de las fuerzas exteriores.
Referencias
- Rañada y Menéndez Luarca, Antonio (1990). Dinámica Clásica. 84-206-8133-4.
- H. Goldstein (1990). Mecánica Clásica. 84-291-4306-8.
Equilibrio de un punto en un campo de fuerzas
Equilibrio estable/inestable
En general la fuerza puede expresarse como
Para analizar las condiciones de equilibrio de un cuerpo puntual en un campo de fuerzas, suponiendo que las fuerzas son funciones matemáticas analíticas, conviene partir del desarrollo de primer orden en función de las coordenadas de posición. El desarrollo se hará, sin pérdida de generalidad, en torno al origen.
Si el cuerpo puntual está en equilibrio la fuerza del campo en el origen se anula. Para que el equilibrio sea además estable la fuerza residual debe tender a devolver el cuerpo al origen para cualquier desplazamiento, es decir tener sentido opuesto al desplazamiento y por tanto
Campos conservativos
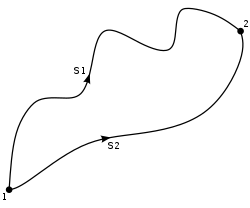
.
Si se trata de un campo conservativo se puede definir una función energía potencial que depende únicamente de la posición. Considerse el trabajo para desplazar el cuerpo de un punto 1 a otro 2 por un camino S1 y de nuevo a A por S2. Por la hipótesis de campo conservativo el trabajo total ha de anularse.
lo que significa que el trabajo no depende de la trayectoria.
Escogiendo arbitrariamente un valor para la energía potencial en un punto dado podemos definir
Calculemos la deriva parcial respecto a x de la funcion energía pontencial, para ello consideremos un pequeño desplazamiento en dicha dirección.
Asumiendo continuidad de la función fuerza, el teorema del valor medio permite escribir
Con
y en el límite
y el gradiente de de la energía potencial es
Condiciones de equilibrio en campos conservativos
Las condiciones de equilibrio en un campo de fuerzas implican que la fuerza se anula en el punto y tiene derivadas parciales negativas. En un campo conservativo en el que se puede definir una función energía potencial esto equivale a que dicha energía potencial tenga las primeras derivadas parciales nulas y las segundas derivadas positivas, que matemáticamente imponen la existencia de un mínimo de energía potencial en punto de equilibrio.
Referencias
- Rañada y Menéndez Luarca, Antonio (1990). Dinámica Clásica. 84-206-8133-4.
Tipo de equilibrio
Física/Estática/Tipo de equilibrio
Rozamiento
Se define como fuerza de rozamiento o fuerza de fricción a la resistencia que se opone al movimiento (fuerza de fricción cinética) o a la tendencia al movimiento (fuerza de fricción estática) de dos superficies en contacto. Se genera debido a las imperfecciones, especialmente microscópicas, entre las superficies en contacto. Estas imperfecciones hacen que la fuerza entre ambas superficies no sea perfectamente perpendicular a éstas, sino que forma un ángulo (el ángulo de rozamiento) con la normal. Por tanto esta fuerza resultante se compone de la fuerza normal (perpendicular a las superficies en contacto) y de la fuerza de rozamiento, paralela a las superficies en contacto.
Leyes del rozamiento para cuerpos sólidos
- La fuerza de rozamiento es de igual dirección y sentido contrario al movimiento del cuerpo.
En el movimiento de un automóvil la fuerza de rozamiento es la responsable de mover el auto hacia adelante y en este caso acompaña al movimiento. El auto no puede ejercer fuerza sobre si mismo.
- La fuerza de rozamiento es prácticamente independiente del área de la superficie de contacto.
- La fuerza de rozamiento depende de la naturaleza de los cuerpos en contacto, así como del estado en que se encuentren sus superficies.
- La fuerza de rozamiento es directamente proporcional a la fuerza normal que actúa entre las superficies de contacto.
- Para un mismo par de cuerpos, el rozamiento es mayor en el momento de arranque que cuando se inicia el movimiento.
- La fuerza de rozamiento es prácticamente independiente de la velocidad con que se desplaza un cuerpo sobre otro.
Formulación matemática
Existen dos tipos de roce: El estático y el cinético o dinámico. El primero es aquel que impide que un objeto inicie un movimiento y es igual a la fuerza neta aplicada sobre el cuerpo, solo que con sentido opuesto (ya que impide el movimiento). El segundo es una fuerza de magnitud constante que se opone al movimiento una vez que éste ya comenzó. En resumen, lo que diferencia a un roce con el otro es que el estático actúa cuando el cuerpo está quieto y el dinámico cuando está en movimiento.
El roce estático es siempre menor o igual al coeficiente de roce entre los dos objetos (número que se mide experimentalmente y está tabulado) multiplicado por la fuerza normal. El roce dinámico, en cambio, es igual al coeficiente de rozamiento, denotado por la letra griega , por la normal en todo instante. No se tiene una idea perfectamente clara de la diferencia entre el rozamiento dinámico y el estático, pero se tiende a pensar que el estático es mayor que el dinámico, porque al permanecer en reposo ambas superficies, pueden aparecer enlaces iónicos, o incluso micro soldaduras entre las superficies. Éste fenómeno es tanto mayor cuanto más perfectas son las superficies. Un caso más o menos común es el del gripaje de un motor por estar mucho tiempo parado (no solo se gripa por una temperatura muy elevada), ya que al permanecer las superficies del pistón y la camisa durante largo tiempo en contacto y en reposo, pueden llegar a soldarse entre sí.
Rozamiento estático
En el caso del rozamiento estático, existe un rango de fuerzas que pueden ser aplicadas al cuerpo y no una única como es el caso del roce dinámico. Para cualquier fuerza que cumpla con la expresión
el cuerpo se mantendrá en reposo
- es el coeficiente de roce estático.
- es la fuerza normal entre ambas superficies.
Valores de los coeficientes de fricción
Coeficiente de rozamiento de algunas sustancias:
| Materiales en contacto | Fricción estática | Fricción cinética |
|---|---|---|
| Articulaciones humanas | 0,22 | 0,003 |
| Hielo // Hielo | 0,1 | 0,03 |
| Vidrio // Vidrio | 0,9 | 0,4 |
| Vidrio // Cuero | 0,3 | 0,25 |
| Vidrio // Madera | 0,53 | 0,4 |
| Madera // Cuero | 0,5 | 0,4 |
| Madera // Piedra | 0,7 | 0,3 |
| Madera // Madera | 0,7 | 0,4 |
| Acero // Madera | 0,6 | 0,3 |
| Acero // Acero | 0,15 | 0,1 |
| Acero // Vidrio | 0,15 | 0,2 |
| Acero // Hielo | 0,03 | 0,02 |
| Acero // Latón | 0,5 | 0,4 |
| Acero // Teflón | 0,04 | 0,04 |
| Teflón // Teflón | 0,04 | 0,04 |
| Caucho // Cemento (seco) | 1,0 | 0,8 |
| Caucho // Cemento (húmedo) | 0,3 | 0,25 |
| Cobre // Hierro (fundido) | 1,1 | 0,3 |
| Esquí (encerado) // Nieve (0ºC) | 0,1 | 0,05 |
Vibraciones Mecánicas
Galileo Galilei
(1563-1641) estudió con detenimiento este fenómeno. Para ello se ayudó de un péndulo, aparato que consta de un hilo y de una esfera u otro cuerpo que esta suspendido de el y oscila libremente. Con sus experimentos Galileo descubrió los principios básicos del MAS.
El movimiento que describe el cuerpo recorre la misma trayectoria cada determinado tiempo. Cuando un cuerpo con este movimiento se desplaza, origina un movimiento ondulatorio.
La materia y la energía están íntimamente relacionadas. La primera está representada por partículas y la segunda por "ondas", aunque hoy en día esa separación no está tan clara. En el mundo subatómico "algo" puede comportarse como partícula u onda según la experiencia que se esté haciendo. Por ejemplo, la electricidad está constituida por electrones y estos presentan este doble comportamiento.
El tipo de movimiento característico de las ondas se denomina movimiento ondulatorio. Su propiedad esencial es que no implica un transporte de materia de un punto a otro. Así, no hay una ficha de dominó o un conjunto de ellas que avancen desplazándose desde el punto inicial al final; por el contrario, su movimiento individual no alcanza más de un par de centímetros. Lo mismo sucede en la onda que se genera en la superficie de un lago o en la que se produce en una cuerda al hacer vibrar uno de sus extremos. En todos los casos las partículas constituyentes del medio se desplazan relativamente poco respecto de su posición de equilibrio. Lo que avanza y progresa no son ellas, sino la perturbación que transmiten unas a otras. El movimiento ondulatorio supone únicamente un transporte de energía y de cantidad de movimiento.
Proceso por el que se propaga energía de un lugar a otro sin transferencia de materia, mediante ondas mecánicas o electromagnéticas. En cualquier punto de la trayectoria de propagación se produce un desplazamiento periódico, u oscilación, alrededor de una posición de equilibrio. Puede ser una oscilación de moléculas de aire, como en el caso del sonido que viaja por la atmósfera, de moléculas de agua (como en las olas que se forman en la superficie del mar) o de porciones de una cuerda o un resorte. En todos estos casos, las partículas oscilan en torno a su posición de equilibrio y sólo la energía avanza de forma continua. Estas ondas se denominan mecánicas porque la energía se transmite a través de un medio material, sin ningún movimiento global del propio medio. Las únicas ondas que no requieren un medio material para su propagación son las ondas electromagnéticas; en ese caso las oscilaciones corresponden a variaciones en la intensidad de campos magnéticos y eléctricos.
Ondas
Las ondas: imaginemos un estanque de agua quieta al que tiramos una piedra, pronto, pero no instantáneamente, se formarán olas. Esas "olas" en realidad son ondas que se propagan desde el centro donde la piedra, al caer, es la "fuente" de perturbaciones circulares. Si llevamos este ejemplo a un parlante, este igual que la piedra, perturba el medio propagándose y alejándose de su fuente. Así como las ondas necesitaban al agua para poder difundirse, el sonido necesita del aire para lograr lo mismo.
Al arrojar una roca a un recipiente con agua (H2O) observamos la propagación de la onda de un lado a otro, por medio del agua, en ella se nota el movimiento ondulatorio.
La onda consta de dos movimientos: uno es la vibración de las partículas y otro es la propagación de la onda en sí. Si el movimiento de cada partícula es " de arriba hacia abajo y viceversa" la onda se llama transversal.. Si la partícula se mueve en la misma dirección de propagación moviéndose atrás y adelante, la onda recibe el nombre de longitudinal.
El sonido es una onda longitudinal mientras que la luz y cualquier onda electromagnética es transversales. Si hacemos ondas con una soga nos dará ondas transversales mientras que un resorte puede transportar ambos tipos de ondas.
Una onda es una perturbación periódica que se propaga en un medio o en el espacio transportando energía. La propagación de una onda involucra el desplazamiento elástico de partículas materiales o cambios periódicos en alguna cantidad física como la presión, la temperatura o los cambios electromagnéticos. Para descubrir una onda se considera: el valle, la cresta, el nodo, frecuencia, longitud de onda, la amplitud y la velocidad de propagación.
Lo que afirma la ley de la conservación de la energía; “La energía ni se crea ni se destruye simplemente se transforma”, la energía puede ser propagada a través del espacio y de la materia por medio de vibraciones, por ejemplo el sonido, la luz, las ondas de radio, esto se comprende estudiando como se forman, como se comportan y como se propagan.
En física una onda es una oscilación que se propaga por el espacio a partir de un medio, transportando energía pero no materia. Una onda es causada por algo que oscila, es decir, que se mueve repetidamente de un lado a otro en torno a una posición central o de equilibrio.
Las ondas son una perturbación periódica del medio en que se mueven. En las ondas longitudinales, el medio se desplaza en la dirección de propagación. Por ejemplo, el aire se comprime y expande (figura 1) en la misma dirección en que avanza el sonido. En las ondas transversales, el medio se desplaza en ángulo recto a la dirección de propagación. Por ejemplo, las ondas en un estanque avanzan horizontalmente, pero el agua se desplaza verticalmente.
Los terremotos generan ondas de los dos tipos, que avanzan a distintas velocidades y con distintas trayectorias. Estas diferencias permiten determinar el epicentro del sismo. Las partículas atómicas y la luz pueden describirse mediante ondas de probabilidad, que en ciertos aspectos se comportan como las ondas de un estanque.
Propagación de las ondas
El mecanismo mediante el cual una onda mecánica monodimensional se propaga a través de un medio material puede ser descripto inicialmente considerando el caso de las ondas en un muelle. Cuando el muelle se comprime en un punto y a continuación se deja en libertad, las fuerzas recuperadoras tienden a restituir la porción contraída del muelle a la situación de equilibrio. Pero dado que las distintas partes del muelle están unidas entre sí por fuerzas elásticas, la dilatación de una parte llevará consigo la compresión de la siguiente y así sucesivamente hasta que aquélla alcanza el extremo final.
En las ondas en la superficie de un lago, las fuerzas entre las moléculas de agua mantienen la superficie libre como si fuera una película tensa. Tales fuerzas de unión entre las partículas componentes son las responsables e que una perturbación producida en un punto se propague al siguiente, repitiéndose el proceso una y otra vez de forma progresiva en todas las direcciones de la superficie del líquido, lo que se traduce en el movimiento de avance de ondas circulares.
Como puede deducirse del mecanismo de propagación descrito, las propiedades del medio influirán decisivamente en las características de las ondas. Así, la velocidad de una onda dependerá de la rapidez con la que cada partícula del medio sea capaz de transmitir la perturbación a su compañera. Los medios más rígidos dan lugar a velocidades mayores que los más flexibles. En un muelle de baja constante elástica k una onda se propagará más despacio que en otra que tenga una k mayor. Lo mismo sucede con los medios más densos respecto de los menos densos.
Ningún medio material es perfectamente elástico. Las partículas que lo forman en mayor o menor grado rozan entre sí, de modo que parte de la energía que se transmite de unas a otras se disipan en forma de calor. Esta pérdida de energía se traduce, al igual que en el caso de las vibraciones, en una atenuación o amortiguamiento. Sin embargo, el estudio de las ondas en las condiciones más sencillas prescinde de estos efectos indeseables del rozamiento.
Características de las ondas
- LONGITUD DE ONDA mecanica
Es la distancia entre una cresta y otra o valles consecutivos.
Parámetro físico que indica el tamaño de una onda. Si se representa la onda como una serie de crestas regulares (una línea ondulada), la longitud de onda sería la distancia entre dos crestas consecutivas. Se representa con la letra griega l (lambda)
En espectroscopia, la longitud de onda es el parámetro usado para definir el tipo de radiación electromagnética, y se mide usualmente en nanómetros. Una longitud de onda corta indica que la radiación es muy energética, y viceversa. Por ejemplo, la longitud de onda de la radiación ultravioleta de una lámpara de las usadas para comprobar billetes es de 254 nanómetros, mientras que la longitud de onda de la radiación infrarroja emitida por una bombilla es de unos 700 nanómetros.
Es la distancia entre dos puntos iguales correspondientes a dos ondas sucesivas. La longitud de onda esta relacionada con la frecuencia V de la onda mediante la formula:
Se expresa en unidades de longitud; metros, centímetros, kilómetros y las longitudes de onda de la luz son de orden de millonésimas de metro (micrometros)
- NODO
Es el punto donde la onda cruza la línea de equilibrio.
- OSCILACIÓN
Se lleva a cabo cuando un punto en vibración ha tomado todos los valores positivos y negativos.
Son los puntos medios que están entre las crestas y los valles en la línea central de los desplazamientos.
- ELONGACIÓN
Es la distancia en forma perpendicular de un punto de la onda a la línea o posición de equilibrio.
- AMPLITUD
Es la distancia entre el punto extremo que alcanza una partícula vibrante y su posición de equilibrio. La amplitud es la máxima elongación.
La amplitud de onda está directamente relacionada con la intensidad de la onda, la amplitud es el ancho de onda, es decir, la distancia que separa a dos crestas o dos valles sucesivos.
- FRECUENCIA:
Es el número de veces que se representa un fenómeno periódico en la unidad de tiempo, es decir, el número de ondas que pasan por segundo. La unidad en la que se mide la frecuencia es el hertz (Hz) en honor a Heinrich Hertz, quien demostró la existencia de las ondas de radio en 1886. Y se calcula como ciclos entre segundos, es decir, el número de veces por segundo que ocurre algún fenómeno.
1 Hz = 1/s
Una vibración por segundo corresponde a una frecuencia de 1 hertz; dos vibraciones por segundo equivalen a 2 hertz, y así sucesivamente. Las grandes frecuencia se miden en kilohertz (kHz) y las frecuencias aún más elevadas en megahetz (MHz). Las ondas de radio de amplitud modulada se transmiten en kilohertz, mientras que las ondas de frecuencia modulada se transmiten en megahertz.
Por ejemplo, una estación ubicada en la posición correspondiente a 960 kHz en la banda de AM emite ondas de radio cuya frecuencia es de 960 000 vibraciones por segundo. Una estación ubicada en la posición de 101 MHz de la banda de FM emite ondas de radio cuya frecuencia es de 101 000 000 hertz. La frecuencia con que vibra la fuente y la frecuencia de las ondas que produce son iguales.
- PERIODO:
Tiempo que tarda un cuerpo que tiene un movimiento periódico –el cual el cuerpo se mueve de un lado a otro, sobre una trayectoria fija-en efectuar un ciclo completo de su movimiento. Su unidad, oscilación, onda, ciclo, vibración, segundo.
RELACIÓN ENTRE FRECUENCIA Y PERIODO
Por ejemplo, un centro emisor produce una onda en ½ segundo, o sea su periodo es de T= ½ segundo y su frecuencia, f, será 2 ondas/segundo.
Lo que significa que f y T son reciprocas, es decir:
- VELOCIDAD DE PROPAGACIÓN
Desplazamiento de una onda en una unidad de tiempo, es decir, habrá realizado una oscilación completa cuando la onda se haya desplazado una longitud de onda. Si el periodo (T) es el tiempo en que el punto considerado tarda en realizar una oscilación, podemos decir que la onda ha avanzado una distancia en un tiempo, es decir: , pero como el periodo T es igual a 1/f, la expresión anterior también podemos expresarla de la siguiente manera: .
Velocidad de propagación es igual al valor de la longitud de onda entre el periodo. Sus unidades son, cm/s, m/s.
La velocidad con que se propague un fenómeno ondulatorio depende de la naturaleza del medio en que se realiza la propagación. Así, la velocidad del sonido no es la misma en el aire que en el agua o que en el acero, ni tampoco la velocidad de la luz en la misma en el vació que en el agua, aire o vidrio. La velocidad de la luz en el vació es igual a 300 000 km/s y es la máxima velocidad que se puede alcanzar en la naturaleza.
Las ondas sonoras por ejemplo, viajan con rapidez de 330 o 350 m/s en el aire (dependiendo la temperatura) y unas cuatro veces mas aprisa en el agua. Cual sea el medio, la rapidez de una onda esta relacionada con su frecuencia y su longitud de onda.
- VALLE
La parte inferior de una onda
- CRESTA
La parte superior de una onda
Tipos de ondas
Dimensiones en que se propaga la onda:
- Unidimensionales.
- Bidimensionales.
- Tridimensionales.
- Cuadimensionales.
Según la dirección de oscilación:
- Longitudinales: la dirección de oscilación y de propagación coinciden (sonido).
- Transversales: las direcciones de vibración y propagación son perpendiculares.
Una onda elástica es una perturbación tensional que se propaga a lo largo de un medio elástico. Por ejemplo las ondas sísmicas ocasionan temblores que pueden tratarse como ondas elásticas que se propagan por el terreno.
Tipos de ondas:
- Onda plana
En general una onda elástica puede ser una combinación de ondas longitudinales y de ondas transversales. Una manera simple de demostrar esto considerar la propagación de ondas planas en las que el vector de desplazamientos provocados por el paso de la onda tiene la forma u = u(x,t)
- Ondas P y S
Una descomposición más general de una onda elástica sirve como ecuación de onda es la descomposición de Helmholtz para campos vectoriales, en una componente longitudinal a lo largo de la dirección del recorrido de la propagación y una onda transversal a la misma. Estas dos componentes se llaman usualmente componente P (onda P o primaria) y componente S (onda S o secundaria).
- Ondas de Rayleigh
Las ondas de Rayleigh son ondas superficiales elípticas, que son una solución de la ecuación de la forma vectorial, cuya amplitud disminuye exponencialmente con la profundidad. Un modelo simple de ondas de Rayleigh es que se da en un medio elástico semi-infinito, que podría representar el terreno.
- Ondas de Love
Las ondas de Love son ondas superficiales, que requieren la existencia de una capa superficial con propiedades mecánicas ligeramente diferente de las capas más profundas.
Ondas longitudinales
Una onda longitudinal es aquella en la que el movimiento de las partículas del medio es paralelo a la dirección de propagación de la onda. Las ondas longitudinales reciben también el nombre de ondas de presión u ondas de compresión. Algunos ejemplos que hay de ondas longitudinales son el sonido y las ondas sísmicas de tipo P generadas en un terremoto.
Si imaginamos un foco puntual generador del sonido, los frentes de onda se desplazan alejándose del foco, transmitiendo el sonido a través del medio de propagación, por ejemplo:el aire.
Por otro lado, cada partícula de un frente de onda cualquiera oscila en dirección de la propagación, esto es, inicialmente es empujada en la dirección de propagación por efecto del incremento de presión provocado por el foco, retornando a su posición anterior por efecto de la disminución de presión provocada por su desplazamiento. De este modo, las consecutivas capas de aire (frentes) se van empujando unas a otras transmitiendo el sonido.
Ondas transversales
Las ondas transversales son las cuales las partículas del medio en que se propagan se mueven transversalmente a la dirección de propagación de la onda. Un ejemplo de ello son las ondas circulares en el agua, ya que se mueven describiendo todas las direcciones del plano sobre la superficie del agua, pero las partículas suben y bajan, no se trasladan según las direcciones que dibujan sobre el eje horizontal. Al igual que las ondas electromagnéticas, no se desplazan en sentido vectorial dentro del medio según las direcciones de propagación. Dicho de otra forma, los campos eléctrico y magnético oscilan perpendicularmente a la dirección de la propagación, es decir, transversalmente. Así, de acuerdo con el movimiento de las partículas del medio podemos decir que en las ondas transversales las partículas del medio vibran perpendicularmente a la dirección de propagación de la onda.
Lo mismo sucede en el caso de una cuerda; cada punto vibra en vertical, pero la perturbación avanza según la dirección de la línea horizontal. Las variaciones en el desplazamiento de los puntos de una cuerda tensa constituyen una onda típicamente transversal. La mal llamada "ola" que se hace en los estadios de fútbol es prácticamente una onda transversal, dado que la gente no se "mueve" de sus asientos (se mueve, pero levantándose y sentándose, no cambiándose a la silla de al lado). Cuando observamos este tipo de festejo deportivo vemos que la masa que forma el público dibuja un movimiento también en sentido horizontal, como si de una serpiente se tratara; ésa es la dirección de propagación de la onda.
Introducción
Una onda estacionaria es una perturbación que cumple la función de onda teniendo la particularidad de que no transmite momento ni energía. Recuerdese que la ecuación de onda unidimensional viene dada por:
La solución general puede escribirse como la suma de dos perturbaciones que se desplazan en sentidos opuestos:
Una onda estacionaria viene dada precisamente por la suma de dos perturbaciones iguales que se desplazan en sentidos opuestos. Como producto de tal interferencia se producen puntos en los que la perturbación se anula para todo instante denominados nodos.
Tratamiento matemático
Caso unidimensional
En este apartado analizaremos el caso de una onda estacionaria armónica en un medio unidimensional. Para empezar emplearemos la solución de la ecuación de ondas obtenida por separación de variables.
La anterior solución puede verificarse por simple sustitución en la ecuación de ondas. Supondremos que la onda está confinada en la región del espacio [0,a] de modo que . Supondremos además que la onda es armónica de modo que nos restringiremos un solo valor de k.
Aplicando las condiciones mencionadas obtenemos
Caso bidimensional
A continuación se estudiará el caso de una onda estacionaria bidimensional armónica confinada en un rectagulo de lados a y b. Análogamente al caso unidimensional la ecuación de ondas en coordenadas rectangulares tendrá la forma:
La solución será analogamente:
La onda esta confinada en un rectangulo de lados a y b de modo que han de cumplirse las condiciones . Si a estas condiciones imponemos que en cada coordenado dispogamos de un modo propio obtenemos:
Ejemplos
Las ondas estacionarias puuedes presentarse en vibraciones unidimensionales, bidimensionales y tridimensionales.
Ondas estacionarias unidimensionales
Si atas una cuerda a un muro y agitas el extremo libre de arriba abajo producirás una onda en la cuerda. El muro es demasiado rígido para agitarse, de modo que la onda se refleja y vuelve hacia ti desplazándose por la cuerda. Agitando la cuerda de cierta manera puedes hacer que la onda incidente (es decir, la onda original) y la onda reflejada formen una onda estacionaria en la que ciertos puntos de la cuerda llamamos nodos permanecen inmóviles. Los puntos de mayor amplitud de una onda estacionaria se conocen como antinodos. Los antinodos están en los puntos medios entre dos nodos.
Las ondas estacionarias son producto de la interferencia. Cuando dos ondas de la misma amplitud y longitud de onda pasan una sobre otra en direcciones contrarias, están siempre fuera de fase en los nodos. Los nodos son regiones estables de interferencia destructiva.
Ondas estacionarias bidimensionales
Cada uno de los modos normales de vibracion de una superficie constituye también una onda estacionaria. De este modo podemos observar ondas estacionarias en la superficie del agua o en la tela de un tambor (si despreciamos los efectos producidos por la atenuación).

Examinado en detalle la figura adyacente, observamos que la distancia entre dos picos (valles) adyacentes es la misma con independencia de cuales sean los picos (valles) escogidos. Esta distancia en la onda idealizada representada como , es la longitud de onda.
En general, la longitud de onda es la distacia de separación entre puntos adyacente en fase (dos puntos están en fase cuando están separados por un número entero de ciclos de onda completos).
Referencias
- FHSST Authors (agosto de 2005). The Free High School Science Texts: A Textbook for High School Students Studying Physics..
http://savannah.nongnu.org/projects/fhsst Las propiedades de las ondas se manifiestan a través de una serie de fenómenos que constituyen lo esencial del comportamiento ondulatorio. Así, las ondas rebotan ante una barrera, cambian de dirección cuando pasan de un medio a otro, suman sus efectos de una forma muy especial y pueden salvar obstáculos o bordear las esquinas.
El estudio de los fenómenos ondulatorios supone la utilización de conceptos tales como periodo, frecuencia, longitud de onda y amplitud, y junto a ellos el de frente de onda, el cual es característico de las ondas bi y tridimensionales.
Se denomina frente de ondas al lugar geométrico de los puntos del medio que son alcanzados en un mismo instante por la perturbación.
Las ondas que se producen en la superficie de un lago, como consecuencia de una vibración producida en uno de sus puntos, poseen frentes de onda circulares. Cada uno de esos frentes se corresponde con un conjunto de puntos del medio que están en el mismo estado de vibración, es decir a igual altura. Debido a que las propiedades del medio, tales como densidad o elasticidad, son las mismas en todas las direcciones, la perturbación avanza desde el foco a igual velocidad a lo largo de cada una de ellas, lo que explica la forma circular y, por tanto, equidistante del foco, de esa línea que contiene a los puntos que se encuentran en el mismo estado de vibración.
Las ondas tridimensionales, como las producidas por un globo esférico que se infla y desinfla alternativamente, poseen frentes de ondas esféricos si el foco es puntual y si el medio, como en el caso anterior, es homogéneo. En física, la interferencia es un fenómeno en el que dos o más ondas se superponen para formar una onda resultante de mayor, menor o igual amplitud. El efecto de interferencia puede ser observado en todos los tipos de onda, como ondas de luz, radio, sonido, entre otros. La ecuación de la onda resultante es la suma algebraica de las funciones de las ondas que se están superponiendo. Se denomina pulsación u oscilación a una variación, perturbación o fluctuación en el tiempo de un medio o sistema. En física, química e ingeniería es el movimiento repetido en torno a una posición central, o posición de equilibrio. Más específicamente que totalmente existe y aparte de todo se suele hablar de vibración cuando la oscilación tiene lugar en un sólido. Este fenómeno de vaivén tan habitual y con orígenes tan dispares, es fácil de reconocer por ejemplo, en el movimiento de un columpio, el péndulo de un reloj, el movimiento de la lengüeta de un instrumento musical de viento o en la forma rizada de la superficie del agua como consecuencia de las ondas que se generan en ella. Se dice que un sistema físico (mecánico, eléctrico, luminoso, etc.) oscila cuando algunos parámetros representativos del mismo (tiempo, posición, velocidad, intensidad eléctrica, tensión eléctrica, elongación, ángulo de giro, intensidad luminosa, etc...) adquieren unos valores que se van repitiendo periódicamente. La explicación de los fenómenos ondulatorios puede hacerse de forma sencilla sobre la base de un principio propuesto por Christian Huygens (1629−1695) para ondas luminosas, pero que es aplicable a cualquier tipo de ondas. La observación de que las ondas en la superficie del agua se propagaran de una forma gradual y progresiva suscitó en Huygens la idea de que la perturbación en un instante posterior debería ser producida por la perturbación en otro anterior. Este fue el germen del siguiente principio general de propagación de las ondas que lleva su nombre:
Cada uno de los puntos de un frente de ondas puede ser considerado como un nuevo foco emisor de ondas secundarias que avanzan en el sentido de la perturbación y cuya envolvente en un instante posterior constituye el nuevo frente.
La aplicación del principio de Huygens se lleva a efecto mediante un método puramente geométrico conocido como método de construcción de Huygens. En el caso de una onda bidimensional circular producida por un foco o fuente puntual la aplicación de este método sería como sigue.
Si S es el frente de ondas correspondiente a un instante cualquiera t, según el principio de Huygens, cada punto de S se comporta como un emisor de ondas secundarias también circulares. Al cabo de un intervalo de tiempo t los nuevos frentes formarán una familia de circunferencias Si, con sus centros situados en cada uno de los puntos de S y cuyo radio r = v • Dt será el mismo para todas ellas si la velocidad v de propagación es igual en cualquier dirección. La línea S' tangente a todos los frentes secundarios Si y que los envuelve resulta ser otra circunferencia y constituye el nuevo frente de ondas para ese instante posterior
La reflexión es el cambio de dirección de una onda al entrar en contacto con la superficie (interfaz) que separa dos medios diferentes. Algunos ejemplos comunes son la reflexión de la luz, el sonido y las ondas de agua. La ley de la reflexión dice que para la reflexión especular (por ejemplo en un espejo) el ángulo con el que la onda incide en la superficie es igual al ángulo con el que se refleja.
La refracción es el cambio de dirección y velocidad que experimenta una onda de luz al pasar de un medio a otro, ya sea líquido o gaseoso, con distinto índice refractivo. Solo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si estos tienen índices de refracción distintos. La refracción se origina en el cambio de velocidad de propagación de la onda señalada. {{:Física/Vibraciones mecánicas/Efecto Doppler|Efecto Doppler]]
Oscilacion armónica libre
Decimos que una partícula está sometida a un potencial armónico unidimensional cuando este es de la forma:
O dicho de otro modo, cuando la fuerza a la que está sometido es del tipo:
Si planteamos la ecuación del movimiento tenemos que:
La solución de la ecuación diferencial es por tanto:
Redefiniendo variables:
siendo
Oscilación armónica amortiguada
A continuación estudiaremos el caso de una partícula sometida a un potencial armónico y que sufre una fuerza de rozamiento proporcional a la velocidad.
La fuerza de rozamiento es de la forma:
La ecuación de movimiento queda por tanto:
La solución en este caso es:
siendo
A continuación analizaremos el movimiento resultante en función del signo del anterior discriminante:
Oscilador con amortiguamiento débil
Suponiendo la condición de que , definimos:
En este caso la solución de la ecuación de movimiento toma la forma:
Redefiniendo variables:
Por tanto, la solución es un movimiento oscilante en torno a la posición de equilibrio cuya amplitud disminuye a medida que transcurre el tiempo.
Oscilación armónica amortiguada y forzada
Vibraciones Acopladas
Las vibraciones acopladas se refieren al fenómeno en el que dos o más sistemas vibrantes interactúan entre sí, lo que resulta en un comportamiento vibratorio complejo. Esta interacción puede manifestarse de diversas maneras, como la transferencia de energía entre los sistemas o la modificación de las frecuencias naturales de vibración. Algunos ejemplos de vibraciones acopladas incluyen:
Vibraciones Forzadas:
Cuando un sistema vibrante transfiere energía a otro sistema cercano, causando que este último vibre a una frecuencia específica.
Resonancia:
Dos sistemas vibrantes pueden influenciarse mutuamente, lo que resulta en una amplificación de la amplitud de las vibraciones en ciertas condiciones.
Modos Normales de Vibración Acoplada:
En sistemas complejos, las vibraciones de los componentes individuales pueden combinarse para formar modos de vibración acoplada, que tienen frecuencias y formas específicas.
El estudio de las vibraciones acopladas es importante en campos como la ingeniería estructural, la física y la acústica, ya que permite comprender y predecir el comportamiento de sistemas complejos en los que interactúan múltiples vibraciones.
Acústica
Sonido
El sonido es una sensación, en el órgano del oído, producida por el movimiento ondulatorio en un medio elástico (normalmente el aire), debido a rapidísimos cambios de presión, generados por el movimiento vibratorio de un cuerpo sonoro.
- Véase: Onda sonora
La función del medio transmisor es fundamental, ya que el sonido no se propaga en el vacío. Por ello, para que exista el sonido, es necesaria una fuente de vibración mecánica y también un medio elástico (sólido, líquido o gaseoso) a través del cual se propague la perturbación. El aire es el medio transmisor más común del sonido. La velocidad de propagación del sonido en el aire es de aproximadamente 343 metros por segundo a una temperatura de 20 ºC (293 Kelvin).
Cuando un objeto (emisor) vibra, hace vibrar también al aire que se encuentra alrededor de él. Esa vibración se transmite a la distancia y hace vibrar (por resonancia) una membrana que hay en el interior del oído, el tímpano, que codifica (convierte) esa vibración en información eléctrica. Esta información se trasmite al cerebro por medio de las neuronas. El cerebro decodifica esa información y la convierte en una sensación. A esa sensación se le denomina "sonido".
Magnitudes físicas del sonido
Como todo movimiento ondulatorio, el sonido puede representarse por una curva ondulante, como por ejemplo una sinusoide y se pueden aplicar las mismas magnitudes unidades de medida que a cualquier Onda mecánica.
A saber:
- Longitud de onda: indica el tamaño de una onda. Entendiendo por tamaño de la onda, la distancia entre el principio y el final de una onda completa (ciclo).
- Frecuencia: número de ciclos (ondas completas) que se producen en una unidad de tiempo. En el caso del sonido la unidad de tiempo es el segundo y la frecuencia se mide en Hercios (ciclos/s).
- Periodo: es el tiempo que tarda cada ciclo en repetirse.
- Amplitud: indica la cantidad de energía que contiene una señal sonora. No hay que confundir amplitud con volumen o potencia acústica.
- Fase: la fase de una onda expresa su posición relativa con respecto a otra onda.
- Potencia: La potencia acústica es la cantidad de energía radiada en forma de ondas por unidad de tiempo por una fuente determinada. La potencia acústica depende de la amplitud.
Potencia acústica
La potencia acústica es la cantidad de energía (potencia) radiada por una fuente determinada en forma de ondas por unidad de tiempo.
La potencia acústica viene determinada por la propia amplitud de la onda, pues cuanto mayor sea la amplitud de la onda, mayor es la cantidad de energía (potencia acústica) que genera.
La potencia acústica es un valor intrínseco de la fuente y no depende del local donde se halle, el valor no varia por estar en un local reverberante o en uno seco.
La medición de la potencia puede hacerse o en la fuente o a cierta distancia de la fuente, midiendo la presión que las ondas inducen en el medio de propagación. En cada caso respectivo se utilizaría la unidad de potencia acústica (que en el SI es el vatio, W) o la unidad de presión (que en el SI es el pascal, Pa).
Nivel de potencia acústica
Parámetro que mide la forma en que es percibida la potencia acústica, es decir, el volumen.
Las personas no perciben de forma lineal el cambio (aumento/disminución) de la potencia conforme se acercan/alejan de la fuente. La percepción de la potencia es una sensación que es proporcional al logaritmo de esa potencia. Esta relación logarítmica es el nivel de potencia acústica:
en donde W1 es la potencia a estudiar, y W0 es la potencia umbral de audición, que expresada en unidades del SI, equivale a vatios o 1 pW, y que se toma como referencia fija.
La unidad para medir este sonido sería el Belio (o Bel) (B), pero como es una unidad muy grande, se utiliza normalmente su submúltiplo, el decibelio (dB), por lo que para obtener el resultado directamente habría que multiplicar el segundo término de la fórmula por 10.
Para sumar sonidos no es correcto sumar los valores de los niveles de potencia o de presión: han de sumarse las potencias o las presiones que los originan. Así, dos fuentes de sonido de 21 dB no dan 42 dB sino 24 dB.
En este caso se emplea la fórmula:
(dB)
O lo que es lo mismo:
(dB)
En las que , es el nivel de presión resultante y son los valores de los niveles de presión a sumar, expresados en decibelios. Las fórmulas convierten los niveles en sus expresiones físicas (potencia o presión y, tras sumar éstas, vuelve a hallar la expresión del nivel sumado.
Características o cualidades del sonido
Las cualidades del sonido son:
- El tono viene determinado por la frecuencia fundamental de las ondas sonoras y es lo que permite distinguir entre sonidos graves, agudos o medios. El tono lo determina la longitud de la onda, medida en ciclos por segundos o Hercios (Hz). Para que podamos percibir los humanos un sonido, éste debe estar comprendido en la franja de 20 y 20.000 Hz. Por debajo tenemos los infrasonidos y por encima los ultrasonidos. A esto se le denomina rango de frecuencia audible. Cuanto mas edad se tiene, este rango va reduciendose tanto en graves como en agudos.
- La intensidad es la cantidad de energía acústica que contiene un sonido. La intensidad viene determinada por la potencia acústica, que a su vez está determinada por la amplitud y nos permite distinguir si el sonido es fuerte o débil. Los sonidos que percibimos deben superar el umbral auditivo (0 dB) y no llegar al umbral de dolor (140 dB). Esta cualidad la medimos con el sonómetro y los resultados se expresan en decibelios (dB).
- El timbre es la cualidad que confiere al sonido los armónicos que acompañan a la frecuencia fundamental. Esta cualidad es la que permite distinguir dos sonidos, por ejemplo, entre la misma nota (tono) con igual intensidad producida por dos instrumentos musicales distintos.
- La duración. Esta cualidad está relacionada con el tiempo de vibración del objeto. Por ejemplo, podemos escuchar sonidos largos, cortos, muy cortos, etc..
Onda sonora
Las variaciones de presión, humedad o temperatura del medio, producen el desplazamiento de las moléculas que lo forman. Cada molécula transmite la vibración a la de su vecina, provocando un movimiento ondulatorio en cadena.
La presión de las partículas que transportan la onda se produce en la misma dirección de propagación del sonido de la onda, siendo por tanto éstas un tipo de ondas longitudinales.
Las ondas sonoras se desplazan también en tres dimensiones y sus frentes de onda son esferas concéntricas que salen desde el foco de la perturbación en todas las direcciones. Por esto son ondas esféricas o tridimensionales.
El hercio (Hz) es la unidad que expresa la cantidad de vibraciones que emite una fuente sonora por unidad de tiempo (frecuencia). El oído humano puede percibir ondas sonoras de frecuencias entre los 16 y los 20.000 Hz. Las ondas que poseen una frecuencia inferior a los 16 Hz se denominan infrasónicas y las superiores a 20.000 Hz, ultrasónicas.
Sonoridad
La sonoridad es una medida subjetiva de la intensidad con la que un sonido es percibido por el oído humano. Es decir, la sonoridad es el atributo que nos permite ordenar sonidos en una escala del más fuerte al más débil.
La unidad que mide la sonoridad es el decibelio.
La sensación sonora de intensidad (sonoridad) se agudiza para sonidos débiles, y disminuye para sonidos fuertes, lo que se debe a que la audición humana no es lineal, sino logarítmica.
Llamamos umbral de audición a la intensidad mínima de sonido capaz de impresionar el oído humano. Su valor se sitúa en 0 dB o 20 micropascales.
Llamamos umbral de dolor a la potencia o intensidad sonora a partir de la cual el sonido produce en el oído sensación de dolor. Su valor medio se sitúa en torno a los 110-130 dB o 100 Pascales.
También podríamos utilizar como unidad de medida el Microbar que es una mil milésima parte de un Bar (magnitud utilizada para medir la presión atmosférica: 1 Bar = 1.000 milibares). Sin embargo es poco práctica, dado que el sonido ejerce en el aire una millonésima parte de presión respecto a la presión atmosférica tomada como punto de equilibrio.
Normalmente, se utiliza la escala en decibelios por una razón obvia, es más manejable utilizar una escala de 0 a 130 (producto de una relación logarítmica) que una que va de la veinte millonésima parte de un pascal a los 100 pascales (producto de una relación lineal).
La sonoridad depende de la intensidad de un sonido, pero también de su frecuencia, amplitud y de otras variables, como pueden ser la sensibilidad del oído de quien escucha y de la duración del sonido.
Como la sonoridad no es una magnitud absoluta, lo que se hace es medir el nivel de sonoridad, es decir, determinar cómo es de fuerte un sonido en relación con otro. Para medir el nivel de sonoridad hay dos unidades: el fonio y el sonio.
Fonio
El fon (o fonio) está definido arbitrariamente como la sonoridad de un sonido senoidal de 1 kHz con un nivel de presión sonora (intensidad) de 0 . Así, 0 dB es igual a 0 fon y 120 dB es igual a 120 fon. Eso siempre para sonidos sinusoidales con frecuencias de 1 kHz.
fonios
El fon es una unidad que no sirve para comparar la sonoridad de dos sonidos diferentes, sino que hace referencia a la sonoridad de un determinado sonido. Lo que se debe a que la escala de fons está relacionada con una escala logarítmica.
Curvas isofónicas
Las curvas isofónicas son curvas de igual sonoridad. Estas curvas calculan la relación existente entre la frecuencia y la intensidad de sonido(en decibelios) de dos sonidos para que éstos sean percibidos como igual de fuertes, con lo que todos los puntos sobre una misma curva isofónica tienen la misma sonoridad.
Así, si 0 fon corresponden a una sonoridad con una intensidad de 0 dB con una frecuencia de 1 kHz, también una sonoridad de 0 fon podría corresponder a una sonoridad con una intensidad de 60 dB con una frecuencia de 70 Hz.
Las primeras curvas de igual sonoridad fueron establecidas por Munson y Fletcher en 1930.

En estas curvas isofónicas se observa como, a medida que aumenta la intensidad sonoras, las curvas se hacen, cada vez, más planas. Esto se traduce en que la dependencia de la frecuencia es menor a medida que aumenta el nivel de presión sonora, lo que significa que si disminuye la intensidad sonora los primeros sonidos en desaparecer serían los agudos (altas frecuencias).
Las curvas de Munson y Fletcher fueron recalculadas, más tarde, por Robinson y Dadson.
Las curvas Munson y Fletcher y las curvas de Robinson y Dadson sólo son válidas para un campo sonoro directo, dado que no tienen en cuenta que no percibimos por igual los sonidos si provienen de diferentes direcciones (campo sonoro difuso).
Otras curvas de ponderación muy difundidas son:
- la curva A (curva de nivel de sonoridad de 30 fon, medidas en decibelios A - ).
- La curva B (curva de nivel de sonoridad de 70 fon, medidas en decibelios B - ).
- La curva C (curva de nivel de sonoridad de 100 fon medidas en decibelios C - ).
El sonio
Como el fon es una unidad que no sirve para comparar la sonoridad de dos sonidos diferentes, se estableció una nueva unidad, el son (o sonio), capaz de establecer la relación real de sonoridad de sonidos diferentes.
El son está definido arbitrariamente como la sonoridad de un sonido senoidal de 1 kHz con un nivel de presión sonora (intensidad) de 40 .
Batimiento
El batimiento es un fenómeno que se genera al superponerse dos ondas sinusoidales con frecuencias ligeramente distintas. La frecuencia de batimiento es igual a la mitad de la diferencia de las frecuencias de las dos ondas. fbat = (f1 - f2) / 2
El batimiento de dos ondas sonoras se percibe como un golpeteo o un vibrato. Un ejemplo familiar de batimiento es el que producen dos cuerdas de guitarra de frecuencias parecidas. Si prestamos atención oiremos un sonido de intensidad muy baja y altura muy grave (casi inaudible).
Batimiento lento
El mínimo de desafinación que un oído humano entrenado puede discriminar es un savart (0,00231 de semitono), que equivale a 4 cents (el cual es una centésima "logarítmica" de semitono, que equivale a 0,00057779).
Si con un instrumento ejecutamos una nota la4 (la quinta tecla blanca a la derecha del do central de un piano), que equivale a 440 hercios (Hz) y con otro instrumento de afinación no fija emitimos simultáneamente una nota la muy ligeramente desafinada, por ejemplo de 439 Hz, escucharemos una resultante parecida a una nota la, pero con un desfase que adoptará la forma de un ligero vibrato (variación de la frecuencia del sonido).
En este ejemplo, este mínimo calamento ('desafinación hacia el grave') perceptible generaría una nota de 438,98 Hz de frecuencia.
fbat = (440,00 Hz - 438,9846 Hz) / 2 = 1,01544 / 2 = 0,5077 Hz
Esto significa que cada 1,9695 segundos se escuchará una variación de la intensidad del sonido (un batimiento).
Batimiento rápido
Cuando el batimiento es muy rápido y está por encima de los 20 Hz (inclusive menos), supera el umbral de audición y el cerebro humano lo comienza a percibir como una frecuencia muy grave, cuya frecuencia es correspondiente a la diferencia de las dos ondas que interactúan.
Es interesante notar que esa tercera frecuencia (el batimiento propiamente dicho) no es real, ya que no puede ser percibida mediante un osciloscopio) sino que es un falso sonido generado por el propio cerebro. Por eso se dice que el batimiento es un fenómeno psicoacústico.
Utilización práctica
Las personas que se dedican a la afinación de pianos utilizan el batimiento para lograr que todas las teclas del piano queden templadas de acuerdo con el "temperamento igual".
El "temperamento igual" fue diseñado para permitir la ejecución de música en todas las tonalidades con una cantidad de igual de desafinación en cada una, mientras que todavía se aproxima a la "entonación justa" (que no permitía cambiar de tonalidad durante una obra, ya que la cantidad de desafinación en algunos intervalos se volvía desagradablemente evidente).
Propagación del sonido
Fenómenos físicos que afectan a la propagación del sonido
Reflexión
Una onda cuando topa con un obstáculo que no puede traspasar se refleja (vuelve al medio del cual proviene).
Una onda se refleja (rebota al medio del cual proviene) cuando topa con un obstáculo que no puede traspasar ni rodear.
El tamaño del obstáculo y la longitud de onda determinan si una onda rodea el obstáculo o se refleja en la dirección de la que provenía.
Si el obstáculo es pequeño en relación con la longitud de onda, el sonido lo rodeara (difracción), en cambio, si sucede lo contrario, el sonido se refleja (reflexión).
Si la onda se refleja, el ángulo de la onda reflejada es igual al ángulo de la onda incidente, de modo que si una onda sonora incide perpendicularmente sobre la superficie reflejante, vuelve sobre sí misma.
La reflexión no actúa igual sobre las altas frecuencias que sobre las bajas. Lo que se debe a que la longitud de onda de las bajas frecuencias es muy grande (pueden alcanzar los 18 metros), por lo que son capaces de rodear la mayoría de obstacúlos.
En acústica esta propiedad de las ondas es sobradamente conocida y aprovechada. No sólo para aislar, sino también para dirigir el sonido hacia el auditorio mediante placas reflectoras (reflectores y tornavoces).
La línea amarilla es el sonido directo, las otras líneas son algunas de las primeras reflexiones.
Fenómenos relacionados con la reflexión
- Las ondas estacionarias. Una onda estacionaria se produce por la suma de una onda y su onda reflejada sobre un mismo eje. Dependiendo como coincidan las fases de la onda incidente y de la reflejada, se producirá una modificacion del sonido (aumenta la amplitud o disminuye), por lo que el sonido resultante puede ser desagradable. En determinadas circunstancias, la onda estacionaria puede hacer que la sala entre en resonancia.
- El eco. La señal acústica original se ha extinguido, pero aún nos es devuelto sonido en forma de onda reflejada. El eco se explica por que la onda reflejada nos llega en un tiempo superior al de la persistencia acústica.
- La reverberación. Se produce reverberación cuando las ondas reflejadas llegan al oyente antes de la extinción de la onda directa, es decir, en un tiempo menor que el de persistencia acústica del oído.
Absorción
Cuando una onda sonora alcanza una superfice, la mayor parte de su energía se refleja, pero un porcentaje de ésta es absorbida por el nuevo medio. Todos los medios absorben un porcentaje de energía que propagan, ninguno es completamente opaco.
En relación con la absorción ha de tenerse en cuenta:
- El coeficiente de absorción que indica la cantidad de sonido que absorbe una superficie en relación con la incidente.
- La frecuencia crítica es la frecuencia a partir de la cual una pared rígida empieza a absorber parte de la energía de las ondas incidentes.
Tipos de materiales en cuanto a su absorción
- Materiales resonantes, que presentan la máxima absorción a una frecuencia determinada: la propia frecuencia del material.
- Materiales porosos, que absorben más sonido a medida de que aumenta la frecuencia. Es decir, absorben con mayor eficacia las altas frecuencias (los agudos). Por ejemplo: la espuma acústica.
- Absorbentes en forma de panel o membrana absorben con mayor eficacia las bajas frecuencias (los graves), que las altas.
- Absorbente Helmholtz Es un tipo de absorbente creado artificialmente que elimina específicamente unas determinadas frecuencias.
Transmisión
En muchos obstáculos planos (los separados de los edificios) una parte de la energía se transmite al otro lado del obstáculo. La suma de la energía reflejada, absorbida y transmitida es igual a la energía sonora incidente (original).
Refracción
Es la desviación que sufren las ondas en la dirección de su propagación, cuando el sonido pasa de un medio a otro diferente. La refracción se debe a que al cambiar de medio, cambia la velocidad de propagación del sonido.
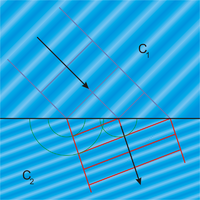
A diferencia de lo que ocurre en el fenómeno de la reflexión en la refracción, el ángulo de refracción ya no es igual al de incidencia.
La refracción se debe a que al cambiar de medio, cambia la velocidad de propagación del sonido.
La refracción también puede producirse dentro de un mismo medio, cuando las características de este no son homogéneas, por ejemplo, cuando de un punto a otro de un medio aumenta o disminuye la temperatura.
Ejemplo: Sobre una superficie nevada, el sonido es capaz de desplazarse atravesando grandes distancias. Esto es posible gracias a las refracciones producidas bajo la nieve, que no es medio uniforme. Cada capa de nieve tiene una temperatura diferente. Las más profundas, donde no llega el sol, están más frías que las superficiales. En estas capas más frías próximas al suelo, el sonido se propaga con menor velocidad.
Difracción o dispersión
Se llama difracción al fenómeno que ocurre cuando el sonido, ante determinados obstáculos o aperturas, en lugar de seguir la propagación en la dirección normal, se dispersa.
La explicación la encontramos en el Principio de Huygens que establece que cualquier punto de un frente de ondas es susceptible de convertirse en un nuevo foco emisor de ondas idénticas a la que lo originó. De acuerdo con este principio, cuando la onda incide sobre una abertura o un obstáculo que impide su propagación, todos los puntos de su plano se convierten en fuentes secundarias de ondas, emitiendo nuevas ondas, denominadas ondas difractadas.
La difracción se puede producir por dos motivos diferentes:
- porque una onda sonora encuentra a su paso un pequeño obstáculo y lo rodea. Las bajas frecuencias son más capaces de rodear los obstáculos que las altas. Esto es posible porque las longitudes de onda en el espectro audible están entre 3 cm y 12 m, por lo que son lo suficientemente grandes para superar la mayor parte de los obstáculos que encuentran.
- porque una onda sonora topa con un pequeño agujero y lo atraviesa.
La cantidad de difracción estará dada en función del tamaño de la propia abertura y de la longitud de onda.
- Si una abertura es grande en comparación con la longitud de onda, el efecto de la difracción es pequeño. La onda se propaga en líneas rectas o rayos, como la luz.
- Cuando el tamaño de la abertura es considerable en comparación con la longitud de onda, los efectos de la difracción son grandes y el sonido se comporta como si fuese una luz que procede de una fuente puntual localizada en la abertura.
En la ilustración, la línea azul representa la difracción; la verde, la reflexión y la marrón, refracción.
Velocidad del sonido
La velocidad del sonido' es la velocidad de propagación de las ondas mecánicas longitudinales, producidas por variaciones de presión del medio. Estas variaciones de presión generan en el cerebro la sensación del sonido. La velocidad de propagación de la onda sonora depende de las características del medio en el que se realiza dicha propagación y no de las características de la onda o de la fuerza que la genera.
Además del interés del estudio del propio sonido, su propagación en un medio puede servir para estudiar algunas propiedades de dicho medio de transmisión. Aunque la velocidad del sonido no depende del tono (frecuencia) ni de la longitud de onda de la onda sonora, sí es importante su atenuación. Este fenómeno se explica por ley cuadrática inversa, que explica que cada vez que se aumenta al doble la distancia a la fuente sonora, la intensidad sonora disminuye.
La velocidad del sonido varía dependiendo del medio a través del cual viajen las ondas sonoras. Varía ante los cambios de temperatura del medio. Esto se debe a que un aumento de la temperatura se traduce en que aumenta la frecuencia con que se producen las interacciones entre las partículas que transportan la vibración y este aumento de actividad hace que aumente la velocidad.
Por ejemplo. sobre una superficie nevada, el sonido es capaz de desplazarse atravesando grandes distancias. Esto es posible gracias a las refracciones producidas bajo la nieve, que no es medio uniforme. Cada capa de nieve tiene una temperatura diferente. Las más profundas, donde no llega el sol, están más frías que las superficiales. En estas capas más frías próximas al suelo, el sonido se propaga con menor velocidad.
En general, la velocidad del sonido es mayor en los sólidos que en los líquidos y en los líquidos mayor que en los gases.
- La velocidad del sonido en el aire (a una temperatura de 20 ºC) es de 340 m/s.
- En el agua es de 1.600 m/s.
- En la madera es de 3.900 m/s.
- En el acero es de 5.100 m/s.
Velocidad de sonido en el aire
En este caso las propiedades físicas del aire, su presión y humedad por ejemplo, son factores que afectan la velocidad.
Por ejemplo, cuanto mayor es la temperatura del aire mayor es la velocidad de propagación. La velocidad del sonido en el aire aumenta 0,6 m/s por cada 1º C de aumento en la temperatura.
Una velocidad aproximada (en metros/segundo) puede ser calculada mediante la siguiente fórmula empírica:
donde es la temperatura en grados celsius (273 kelvins)(c+273=k);
- .
Una ecuación más exacta, referida normalmente como velocidad adiabática del sonido, viene dada por la fórmula siguiente:
donde
- R es la constante de los gases,
- m es el peso molecular promedio del aire (R/m = 287 J/kg K] para el aire),
- κ es la razón de los calores específicos (κ=cp/cv siendo igual a 1,4 para el aire), y
- T es la temperatura absoluta en Kelvin.
En una atmósfera estándar se considera que T es 293,15 Kelvin, dando un valor de 343 m/s ó 1.235 kilómetros/hora. Esta fórmula supone que la transmisión del sonido se realiza sin pérdidas de energía en el medio, aproximación muy cercana a la realidad.
Velocidad de sonido en el agua
La velocidad del sonido en el agua es de interés para realizar mapas del fondo del océano. En agua salada, el sonido viaja a aproximadamente 1.500 m/s y en agua dulce a 1.435 m/s. Estas velocidades varían debido a la presión, profundidad, temperatura, salinidad y otros factores.
Efecto Doppler

El efecto Doppler, llamado así por Christian Andreas Doppler, consiste en la variación de la longitud de onda de cualquier tipo de onda emitida o recibida por un objeto en movimiento. Doppler propuso este efecto en 1842 en una monografía titulada Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels ("Sobre el color de la luz en estrellas binarias y otros astros").
Su hipótesis fue investigada en 1845 para el caso de ondas sonoras por el científico holandés Christoph Hendrik Diederik Buys Ballot, confirmando que el tono de un sonido emitido por una fuente que se aproxima al observador es más agudo que si la fuente se aleja. Hippolyte Fizeau descubrió independientemente el mismo fenómeno en el caso de ondas electromagnéticas en 1848. En Francia este efecto se conoce como "Efecto Doppler-Fizeau".

Hay ejemplos cotidianos de efecto Doppler en los que la velocidad a la que se mueve el objeto que emite las ondas es comparable a la velocidad de propagación de esas ondas. La velocidad de una ambulancia (50 km/h) no es insignificante respecto a la velocidad del sonido al nivel del mar (unos 1.235 km/h), por eso se aprecia claramente el cambio del sonido de la sirena desde un tono más agudo a uno más grave, justo en el momento en que el vehículo pasa al lado del observador.
Álgebra del efecto Doppler en ondas sonoras
Imaginemos que un observador O se mueve hacia una fuente S que se encuentra en reposo. El medio es aire y se encuentra en reposo. El observador O comienza a desplazarse hacia la fuente con una velocidad . La fuente de sonido emite un sonido de velocidad , frecuencia f y longitud de onda . Por lo tanto, la velocidad de las ondas respecto del observador no será la v del aire, sino la siguiente:
. Sin embargo, no debemos olvidar que como el medio no cambia, la longitud de onda será la misma, por lo tanto si:
Pero como mencionamos en la primera explicación de este efecto, el observador al acercarse a la fuente oirá un sonido más agudo, esto implica que su frecuencia es mayor. A esta frecuencia mayor captada por el observador se la denomina frecuencia aparente y la simbolizaremos con f'.
El observador escuchará un sonido de mayor frecuencia debido a que
Analicemos el caso contrario:
Cuando el observador se aleje de la fuente, la velocidad v' será y de manera análoga podemos deducir que . En este caso la frecuencia aparente percibida por el observador será menor que la frecuencia real emitida por la fuente, lo que genera que el observador perciba un sonido de menor altura o más grave.
De estas dos situaciones concluimos que cuando un observador se mueve con respecto a una fuente en reposo, la frecuencia aparente percibida por el observador es:
Ahora consideraremos el caso donde el observador se encuentra en reposo y la fuente se mueve. Cuando la fuente se desplace hacia el observador, los frentes de onda estarán más cerca uno del otro. En consecuencia, el observador percibe sonidos con una menor longitud de onda. Esta diferencia de longitud de onda puede expresarse como:
Por tanto, la longitud de onda percibida será:
Como podemos deducir que:
Haciendo un razonamiento análogo para el caso contrario (fuente alajándose), podemos concluir que la frecuencia percibida por un observador en reposo con una fuente en movimiento será:
Cuando la fuente se acerque al observador se pondrá un (-) en el denominador, y cuando la fuente se aleje se lo reemplazará por un (+).
Al terminar de leer lo anteriormente expuesto surge la siguiente pregunta: ¿Qué pasará si la fuente y el observador se mueven al mismo tiempo?. En este caso particular se aplica la siguiente formula, que no es más que una combinación de las dos:
Los signos y deben ser respetados de la siguiente manera. Si en el numerador se suma, en el denominador debe restarse y viceversa.
Ejemplo:
Un observador se mueve con una velocidad de 42 m/s hacia un trompetista en reposo emitiendo la nota La a 440 Hz. ¿Qué frecuencia percibirá el observador? (Dato: ).
Resolución: Si el observador se acerca hacia la fuente, esto implica que la velocidad con que percibirá cada frente de onda será mayor, por lo tanto la frecuencia aparente será mayor a la real. Para que esto ocurra debemos aplicar el signo (+) en la ecuación.
En este caso particular, el trompetista toca la nota La a 440 Hz, sin embargo el observador percibe una nota que vibra a una frecuencia de 493,88 Hz, que es la frecuencia perteneciente a la nota Si. Musicalmente hablando, el observador percibe el sonido un tono más arriba del que se emite realmente.
Estructura de la materia
- Estructura de la materia
- Estados de la materia
- Estructura intermolecular
- Movimiento molecular. Temperatura. Energía interna
- Termómetros
- Presión
- Dilatación
- Instrumental para determinar densidad
Estados de la materia

Para un cuerpo o agregado material considerado, se observa que modificando las condiciones de temperatura, presión o volumen se pueden obtener distintos estados de agregación, denominados estados de agregación de la materia, con características peculiares.
Estado sólido
Así, manteniendo constante la presión, a baja temperatura los cuerpos se presentan en forma sólida tal que los átomos se encuentran entrelazados formando generalmente estructuras cristalinas, lo que confiere al cuerpo la capacidad de soportar fuerzas sin deformación aparente; son por tanto agregados generalmente rígidos, duros y resistentes.
También señalaremos que los sólidos presentan propiedades específicas:
- Elasticidad: Un sólido recupera su forma original cuando es deformado. Un elástico o un resorte son objetos en los que podemos observar esta propiedad. Estira un elástico y observa lo que sucede.
- Fragilidad: Un sólido puede romperse en muchos pedazos (quebradizo). En más de una ocasión habrás quebrado un vaso de vidrio o un objeto de arcilla. Estos hechos representan la fragilidad de un sólido.
- Dureza: Un sólido es duro cuando no puede ser rayado por otro más blando. El diamante de una joya valiosa o el utilizado para cortar vidrios presenta dicha propiedad.
Estado líquido
Incrementando la temperatura el sólido se va descomponiendo hasta desaparecer la estructura cristalina alcanzándose el estado líquido, cuya característica principal es la capacidad de fluir y adaptarse a la forma del recipiente que lo contiene. En este caso, aún existe una cierta ligazón entre los átomos del cuerpo, aunque de mucha menor intensidad que en el caso de los sólidos.
Estado gaseoso
Por último, incrementando aún más la temperatura se alcanza el estado gaseoso. Los átomos o moléculas del gas se encuentran virtualmente libres de modo que son capaces de ocupar todo el espacio del recipiente que lo contiene, aunque con mayor propiedad debería decirse que se distribuye o reparte por todo el espacio disponible.
Estado Plasmático
Al plasma se le llama a veces "el cuarto (4) estado de la materia", además de los tres conocidos, sólido, líquido y gas. Es un gas en el que los átomos se han roto, que está formado por electrones negativos y por iones positivos, átomos que han perdido electrones y han quedado con una carga eléctrica positiva y que están moviéndose libremente.
Donde vivimos nosotros, en la baja atmósfera, cualquier átomo que pierde un electrón (p.e., cuando es alcanzado por una partícula cósmica rápida) lo recupera pronto o atrapa otro. Pero la situación a altas temperaturas, como las que existen en el Sol, es muy diferente.
Cuanto más caliente está el gas, más rápido se mueven sus moléculas y átomos, y a muy altas temperaturas las colisiones entre estos átomos moviéndose muy rápidamente son lo suficientemente violentas como para liberar los electrones. En la atmósfera solar, una gran parte de los átomos están permanentemente "ionizados" por estas colisiones y el gas se comporta como un plasma.
A diferencia de los gases fríos (p.e. el aire a la temperatura ambiente), los plasmas conducen la electricidad y son fuertemente influidos por los campos magnéticos.
La lámpara fluorescente, muy usada en el hogar y en el trabajo, contiene plasma (su componente principal es el vapor de mercurio) que calienta y agita la electricidad, mediante la línea de fuerza a la que está conectada la lámpara. La línea hace positivo eléctricamente a un extremo y el otro negativo, causa que los iones (+) se aceleren hacia el extremo (-), y que los electrones (-) vayan hacia el extremo (+). Las partículas aceleradas ganan energía, colisionan con los átomos, expulsan electrones adicionales y así mantienen el plasma, incluso aunque se recombinen partículas. Las colisiones también hacen que los átomos emitan luz y, de hecho, esta forma de luz es más eficiente que la de las lámparas tradicionales. Los letreros de neón y las luces urbanas funcionan por un principio similar y también se usan (o usaron) en electrónica.
| Lámpara fluorescente: En el caso de que se pregunte: cuando se enciende por primera vez la lámpara fluorescente, el gas está frío, pero unos pocos iones y electrones están siempre presentes debido a los rayos cósmicos y a la radioactividad natural. Las colisiones los multiplican rápidamente.
Dado que se usa corriente alterna, los puntos (+) y (-) se alternan 60 veces cada segundo. Sin embargo, los iones y electrones responden mucho más rápido que eso, por lo que el proceso permanece el mismo. |
Como ya se dijo, el Sol está formado por plasma. Otro importante plasma en la naturaleza es la ionosfera, que comienza a unos 70-80 km por encima de la superficie terrestre. Aquí los electrones son expulsados de los átomos por la luz solar de corta longitud de onda, desde la ultravioleta a los rayos X: no se recombinan fácilmente debido a que la atmósfera se rarifica más a mayores altitudes y no son frecuentes las colisiones. La parte inferior de la ionosfera, la "capa D", a los 70-90 km, aún tiene suficientes colisiones como para desaparecer después de la puesta del sol. Entonces se combinan los iones y los electrones, mientras que la ausencia de luz solar no los vuelve a producir. No obstante, esta capa se restablece después del amanecer. Por encima de los 200 km, las colisiones son tan infrecuentes que la ionosfera prosigue día y noche.
- Perfil de la ionosfera
La parte superior de la ionosfera se extiende en el espacio muchos miles de kilómetros y se combina con la magnetosfera, cuyos plasmas están generalmente más rarificados y también más calientes. Los iones y los electrones del plasma de la magnetosfera provienen en parte de la ionosfera que está por debajo y en parte del viento solar y muchos de los pormenores de su entrada y calentamiento no están aún claros.
Finalmente, existe el plasma interplanetario, el viento solar. la capa más externa del Sol, la corona, está tan caliente que no solo están todos sus átomos ionizados, sino que aquellos que comenzaron con muchos electrones tienen arrancados la mayoría (a veces la totalidad), incluidos los electrones de las capas más profundas que están más fuertemente unidos. Por ejemplo, en la corona se ha detectado la luz característica del hierro que ha perdido 13 electrones.
Esta temperatura extrema también evita que el plasma de la corona permanezca cautivo por la gravedad solar y así fluye en todas direcciones, llenando el sistema solar más allá de los planetas más distantes. El Sol, mediante el viento solar configura el distante campo magnético terrestre y el rápido flujo del viento (~400 km/s) proporciona la energía que alimenta los fenómenos de la aurora polar, los cinturones de radiación y de las tormentas magnéticas.
Condensado de Bose-Einstein
Otro estado de la materia es el condensado de Bose-Einstein (CBE), predicho en 1924 por Satyendra Nath Bose y Albert Einstein, y obtenido en 1995 (los físicos Eric A. Cornell, Carl E. Wieman y Wolfgang Ketterle compartieron el Premio Nobel de Física de 2001 por este hecho). Este estado se consigue a temperaturas cercanas al cero absoluto y se caracteriza porque los átomos se encuentran todos en el mismo lugar, formando un superátomo.
| Un ejemplo sería: Si pudiéramos sentar a cien personas en una misma silla, pero no una encima de la otra, sino que ocupando el mismo espacio, estaríamos en presencia del condensado de Bose-Einstein. |
Cambios de estado
Los cambios de estado descritos también se producen si se incrementa la presión manteniendo constante la temperatura, así, por ejemplo, el hielo de las pistas se funde por efecto de la presión ejercida por el peso de los patinadores haciendo el agua líquida así obtenida de lubricante y permitiendo el suave deslizamiento de los patinadores.
Para cada elemento o compuesto químico existen unas determinadas condiciones de presión y temperatura a las que se producen los cambios de estado, debiendo interpretarse, cuando se hace referencia únicamente a la temperatura de cambio de estado, que ésta se refiere a la presión de 1 atm (la presión atmosférica). De este modo, en condiciones normales (presión atmosférica y 20 ºC) hay compuestos tanto en estado sólido como líquido y gaseoso.
Estructura intermolecular
Teoría atómica
El paradigma científico actual sobre la constitución de la materia es la Teoría Atómica, según la cual los átomos son las partículas o corpúsculos más pequeños en que se puede dividir la materia ordinaria.
El átomo se compone de un núcleo de carga positiva formado por protones y neutrones, en conjunto conocidos como núcleones, alrededor del cual se encuentra una nube de electrones de carga negativa.
Moléculas

Los átomos se combinan para formar moléculas, cuyos átomos constituyentes se mantienen unidos por las denominadas fuerzas intermoleculares, que provienen de las fuerzas electromagnéticas residuales entre los protones y electrones de los átomos y son el fundamento de los enlaces químicos.
Dado que los núcleos atómicos son miles de veces más pesados que los electrones que los rodean y son por tanto más difícilmente desplazables las fuerzas interatómicas que aparecen al combinar átomos neutros se deben al desplazamiento de los electrones.
Enlaces químicos
Se distinguen dos tipos fundamentales de enlacen químicos, según los electrones se desplacen completamente de un átomo a otro (enlace iónico) o se compartan entre átomos (enlace covalente). Cuando los electrones se comparten entre muchos átomos se forma el enlace metálico.
Enlace iónico

Al desplazarse los electrones de un átomo a otro se forman iones de carga contraria: un catión (de carga positiva) y un anión (de carga negativa). La diferencia entre las cargas de los iones provoca entonces una fuerza de interacción electromagnética entre los átomos que los mantiene unidos.
En una solución, los enlaces iónicos pueden romperse y se considera entonces que los iones están disociados. Es por eso que una solución fisiológica de cloruro de sodio y agua se marca como "Na+ + Cl- " mientras que los cristales de cloruro de sodio se marcan "Na+Cl- " o simplemente "NaCl".
Algunas características de los compuestos formados por este tipo de enlace son:
- Forman redes cristalinas separadas entre sí.
- Altos puntos de fusión.
- Están formados por metales y no metales.
- Son solubles en disolventes polares.
- Una vez fundidos o en solución acuosa, sí conducen la electricidad.
- En estado sólido no conducen la electricidad. Si utilizamos un bloque de sal como parte de un circuito en lugar del cable, el circuito no funcionará. Así tampoco funcionará una bombilla si utilizamos como parte de un circuito un cubo de agua, pero si disolvemos sal en abundancia en dicho cubo, la bombilla, del extraño circuito, se encenderá. Esto se debe a que los iones disueltos de la sal son capaces de acudir al polo opuesto ( a su signo ) de la pila del circuito y por ello este funciona.
Enlace covalente
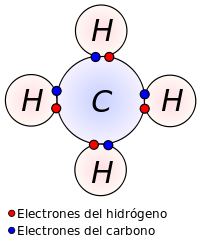
En general, cuando los átomos son distintos, los electrones compartidos no serán atraídos por igual, de modo que estos tenderán a aproximarse hacia el átomo más electronegativo, es decir, aquel que tenga una mayor apetencia de electrones. Este fenómeno se denomina polaridad (los átomos con mayor electronegatividad obtienen una polaridad más negativa, acercando los electrones compartidos hacia su núcleo), y resulta en un desplazamiento de las cargas dentro de la molécula.
Se podría decir que al átomo más electronegativo no le gusta mucho compartir sus electrones con los demás átomos, y en el caso más extremo, deseará que el electrón le sea cedido sin condiciones formándose entonces un enlace iónico, de ahí que se diga que los enlaces covalentes polares tienen, en alguna medida, carácter iónico.
Como propiedades de los compuestos formados por este tipo de enlace destacan:
- Forman redes cristalinas separadas entre sí.
- Bajos puntos de fusión en compuestos de pocos átomos, pero es alto para sólidos covalentes macromoleculares.
- Están formados por no metales.
- Son solubles en disolventes polares.
- Su capacidad conductora es prácticamente nula.
Enlace metálico

El enlace metálico es característico de los elementos metálicos, es un enlace fuerte, primario, que se forma entre elementos de la misma especie.
Los átomos, al estar tan cercanos unos de otros, interaccionan los núcleos junto con sus nubes electrónicas empaquetándose en las tres dimensiones, por lo que quedan rodeados de tales nubes. Estos electrones libres son los responsables de que los metales presenten una elevada conductividad eléctrica y térmica, ya que estos se pueden mover con facilidad si se ponen en contacto con una fuente eléctrica. Presentan brillo y son maleables.
Las características básicas de los elementos metálicos son producidas por la naturaleza del enlace metálico. Entre ellas destacan:
- Suelen ser sólidos a temperatura ambiente pero hay casos en los que no como el Hg (Mercurio) y el Fr (Francio) que son líquidos.
- Sus puntos de fusión suelen ser elevados.
- Las conductividades térmicas y eléctricas son muy elevadas. (esto se explica por la enorme movilidad de sus electrones de valencia)
- Presentan brillo metálico.
- Son dúctiles y maleables. (la enorme movilidad de los electrones de valencia hace que los cationes metálicos puedan moverse sin producir una situación distinta, es decir, una rotura)
- Pueden emitir electrones cuando reciben energía en forma de calor.
- Tienden a perder electrones de sus últimas capas cuando reciben cuantos de luz (fotones), fenómeno conocido como efecto fotoeléctrico.
Movimiento molecular. Temperatura. Energía interna
Movimiento molecular
- Estado gaseoso. Interacción débil, movimiento de las moléculas casi independiente entre sí.
- Estado líquido. Interacción media, pero sin ningún tipo de ligadura de la molécula a una posición espacial concreta.
- Estado sólido. Interacción fuerte. Las moléculas sólo se desplazan en torno a una posición de equilibrio.
Energía interna
En un sistema de moléculas podemos separar la energía cinética entre la energía cinética del centro de masas y la del movimiento relativo. La primera es perceptible y medible macroscópicamente, pero la segunda no, permanece oculta, pero no desaparece. A este tipo de energía no medible macrocópicamente de forma directa, mediante medios mecánicos, la denominamos energía interna del sistema.
Temperatura
Consideraciones iniciales
conocido como ley cero de la Termodinámica enuncia que si un cuerpo A está en equilibrio térmico con otro B que a su vez lo está con C, entonces A está también en equilibrio térmico con C. Este principio permite introducir el concepto de temperatura (T), que caracteriza la capacidad de un cuerpo de transmitir, espontáneamente, calor a otro. Supongamos dos cuerpos A y B en contacto térmico, entonces las relaciones entre las temperaturas de ambos tienen las siguientes posibilidades:
- A transfiere calor a B,
- No hay transferencia de calor,
- A recibe calor de B,
La temperatura es una magnitud que no depende del cuerpo concreto, es una magnitud bien definida.
Demostración de la existencia de la temperatura empírica de un sistema en base a la ley cero
Para dos sistemas en equilibrio termodinámico () representados por sus respectivas coordenadas termodinámicas (X1,Y1) y (X2,Y2) tenemos que dichas coordenadas no son función del tiempo, por lo tanto es posible hallar una función que relacione dichas coordenadas, es decir:
Sean tres sistemas hidrostáticos, A,B,C, representados por sus respectivas termodinámicas: (Pa,Va), (Pb,Vb),(Pc,Vc). Si A y C están en equilibrio debe existir una función tal que:
Es decir:
Donde las funciones y dependen de la naturaleza de los fluidos.
Análogamente, para el equilibrio de los fluidos B y C:
Es decir:
Con las mismas consideraciones que las funciones y dependen de la naturaleza de los fluidos.
La condición dada por la ley cero de la termodinámica de que el equilibrio térmico de A con C y de B con C implica asimismo el quilibrio de A y B puede expresarse matemáticamente como:
Lo nos conduce a la siguiente expresión:
Entonces, llegamos a la conclusión de que las funciones y deben ser de naturaleza tal que se permita la eliminación de la variable termodinámica comón . Una posibilidad, que puede demostrarse única, es:
Asimismo:
Una vez canceladas todas las partes que contienen a podemos escribir:
Mediante una simple repetición del argumento, tenemos que:
Y así sucesivamente para cualquier número de sistemas en equilibrio termodinámico.
Henos demostrado que para todos los sistemas que se hallen en equilibrio termodinámico entre si, existen sendas funciones cuyos valores numéricos son iguales para cada uno de dichos sistemas en equlibrio. Este valor numérico puede ser representado con la letra griega θ y será definido como la temperatura empírica de los sistemas en equilibrio termodinámico.
Así, tenemos que todo equilibrio termodinámico entre dos sistemas es equivalente a un equilibrio térmico de los mismos, es decir, a una igualdad de temperaturas empíricas de estos.
Termómetros

El termómetro es un instrumento de medición de la temperatura que usa el principio de la dilatación, por lo que se prefiere el uso de materiales con un coeficiente de dilatación alto de modo que, al aumentar la temperatura, la dilatación del material sea fácilmente visible.
El creador del primer termoscopio fue Galileo Galilei; éste podría considerarse el predecesor del termómetro. Consistía en un tubo de vidrio que terminaba con una esfera en su parte superior que se sumergía dentro de un líquido mezcla de alcohol y agua. Al calentar el agua, ésta comenzaba a subir por el tubo.
Sanctorius Sanctorius incorporó una graduación numérica al instrumento de Galilei, con lo que surgió el termómetro.
Escalas de temperatura

La escala más usada en la mayoría de los países es la escala centígrada, denominación usual renombrada como Celsius en 1948, en honor a Anders Celsius (1701 - 1744).
Otras escalas usadas en la fabricación de termómetros son:
- Fahrenheit, una unidad de temperatura propuesta por Gabriel Fahrenheit en 1724
- Réaumur, en desuso
- Kelvin o temperatura absoluta, usada casi exclusivamente en laboratorios, la cual se corresponde con una propiedad intrínseca de la materia.
Tipos de termómetros más usados

- Termómetro de vidrio: es un tubo de vidrio sellado que contiene un líquido, generalmente mercurio o alcohol, cuyo volumen cambia con la temperatura de manera uniforme. Este cambio de volumen se visualiza en una escala graduada que por lo general está dada en grados celsius. El termómetro de mercurio fue inventado por Farenheit en el año 1714.
- Termómetro de resistencia: consiste en un alambre de platino cuya resistencia eléctrica cambia cuando cambia la temperatura.
- Termopar: un termopar es un dispositivo utilizado para medir temperaturas basado en la fuerza electromotriz que se genera al calentar la soldadura de dos metales distintos.
- Pirómetro: los pirómetros se utilizan para medir temperaturas elevadas.
- Termómetro de lámina bimetálica, formado por dos láminas de metales de coeficientes de dilatación muy distintos y arrollados dejando el de coeficiente más alto en el interior. Se utiliza sobre todo como censor de temperatura en el termohigrógrafo

Termómetros especiales
Para medir ciertos parámetros se emplean termómetros modificados, tales como:
- El termómetro de globo, para medir la temperatura radiante. Consiste en un termómetro de mercurio que tiene el bulbo dentro de una esfera de metal hueca, pintada de negro de humo. La esfera absorbe radiación de los objetos del entorno más calientes que el aire y emite radiación hacia los más fríos, dando como resultado una medición que tiene en cuenta la radiación. Se utiliza para comprobar las condiciones de comodidad de las personas.
- El termómetro de bulbo húmedo, para medir el influjo de la humedad en la sensación térmica. Junto con un termómetro ordinario forma un psicrómetro, que sirve para medir humedad relativa, tensión de vapor y punto de rocío. Se llama de bulbo húmedo porque de su bulbo o depósito parte una muselina de algodón que lo comunica con un depósito de agua. Este depósito se coloca al lado y más bajo que el bulbo, de forma que por capilaridad está continuamente mojado.
- El termómetro de máxima y el termómetro de mínima utilizado en meteorología.
Presión
En física y disciplinas afines el término presión, también llamada presión absoluta en aquellos casos que es necesario evitar interpretaciones ambiguas, se define como la fuerza por unidad de superficie:
donde: P es la presión, dF es la fuerza normal y dA es el área.
En el Sistema Internacional de Unidades se mide en newton por metro cuadrado, unidad derivada que se denomina pascal.
Además, en determinadas aplicaciones la presión se mide no como la presión absoluta sino como la presión por encima de la presión atmosférica, denominándose presión relativa, presión normal, presión de gauge o presión manométrica. Consecuentemente, la presión absoluta es la presión atmosférica más la presión manométrica (presión que se mide con el manómetro).
Las obsoletas unidades manométricas de presión, como los milímetros de mercurio, están basadas en la presión ejercida por el peso de algún tipo estándar de fluido bajo cierta gravedad estándar. Las unidades de presión manométricas no deben ser utilizadas para propósitos científicos o técnicos, debido a la falta de repetibilidad inherente a sus definiciones. También se utilizan los milímetros de columna de agua (mm.c.d.a.): 1 mm.c.d.a. = 10Pa.
La densidad de fuerza f (= ∂F/∂V) es igual al gradiente de la presión: ; si hace referencia a la fuerza gravitacional, la densidad de la fuerza es el peso específico.
Unidades de presión y sus factores de conversión
La presión atmosférica es de aproximadamente de 101.325 pascales.
| Pascal | bar | N/mm² | kp/m² | kp/cm² (=1 at) | atm | Torr | |
|---|---|---|---|---|---|---|---|
| 1 Pa (N/m²)= | 1 | 10-5 | 10-6 | 0.102 | 0.102×10-4 | 0.987×10-5 | 0.0075 |
| 1 bar (daN/cm²) = | 100000 | 1 | 0.1 | 10200 | 1.02 | 0.987 | 750 |
| 1 N/mm² = | 106 | 10 | 1 | 1.02×105 | 10.2 | 9.87 | 7500 |
| 1 kp/m² = | 9.81 | 9.81×10-5 | 9.81×10-6 | 1 | 10-4 | 0.968×10-4 | 0.0736 |
| 1 kp/cm² (1 at) = | 98100 | 0.981 | 0.0981 | 10000 | 1 | 0.968 | 736 |
| 1 atm (760 Torr) = | 101325 | 1.013 | 0.1013 | 10330 | 1.033 | 1 | 760 |
| 1 Torr (mmHg) = | 133 | 0.00133 | 1.33×10-4 | 13.6 | 0.00132 | 0.00132 | 1 |
Propiedades de la presión en un medio fluido
Primera propiedad
La presión en un punto de un fluido en reposo es igual en todas las direcciones (principio de Pascal)
Segunda propiedad
La presión en todos los puntos situados en un mismo plano horizontal en el seno de un fluido en reposo es la misma.
Tercera propiedad
En un fluido en reposo la fuerza de contacto que ejerce en el interior del fluido una parte de este sobre la otra es normal a la superficie de contacto.
Corolario: En un fluido en reposo la fuerza de contacto que ejerce el fluido sobre la superficie sólida que lo contiene es normal a esta.
Cuarta propiedad
La fuerza de la presión en un fluido en reposo se dirige siempre hacia el interior del fluido, es decir es una compresión, jamás una tracción.
Quinta propiedad
La superficie libre de un líquido en reposo es siempre horizontal.
Dilatación
Bases del fenómeno
La dilatación térmica tiene un fundamento físico diferente en líquidos, gases y sólidos.
En los gases las moléculas están deslocalizadas, por lo que a lo largo del tiempo una molécula puede llegar a ocupar cualquier posición en el seno de la masa gaseosa, el calentamiento produce un aumento de la energía cinética de cada molécula lo cual aumenta la presión del mismo, que a su vez es el fundamento de la dilatación térmica.
En los sólidos antes de la fusión o aparición de deformaciones por calor, cada molécula está constreñida a moverse alrededor de una pequeña región alrededor de la posición de equilibrio de la misma. Al aumentar la temperatura la molécula realiza oscilaciones alrededor de su posición de equilibrio lo cual tiene el efecto de expandir el sólido.
En los líquidos el proceso es más complejo y presenta características intermedias entre gases y líquidos.
Coeficientes de dilatación
Se denomina coeficiente de dilatación al cociente que mide el cambio relativo de longitud, superficie o volumen que se produce cuando un cuerpo sólido o un fluido experimenta un cambio de temperatura.
Para sólidos el tipo de coeficiente de dilatación más comúnmente usado es el coeficiente de dilatación lineal αL. Para una dimensión lineal cualquiera se puede medir experimentalmente comparando el valor de dicha magnitud antes y después de cierto cambio de temperatura como:
En gases y líquidos es más común usar el coeficiente de dilatación volumétrico αV, que viene dado por la expresión:
Para sólidos también puede medirse la dilatación térmica, aunque resulta menos importante en la mayoría de aplicaciones técnicas.
Dilatación lineal
El cambio total de longitud de la dimensión lineal que se considere, expresarse como:
Donde:
- α=coeficiente de dilatación lineal [1/C°]
- L0= Longitud inicial del cuerpo.
- Lf= Longitud final del cuerpo.
- T0= Temperatura inicial del cuerpo.
- Tf= Temperatura final del cuerpo.
Dilatación superficial
La dilatación superfical de un sólido isótropo tiene un coeficiente de dilatación superficial que es aproximadamente dos veces el coeficiente de dilatación lineal. Por ejemplo si se considera una placa rectangular (de dimensiones: Lx y Ly), y se somete a un incremento uniforme de temperatura, el cambio de superficial vendrá dado por:
Dilatación volumétrica
Un sólido isótropo tiene un coeficiente de dilatación volumétrico que es aproximadamente tres veces el coeficiente de dilatación lineal. Por ejm si se considera un pequeño prisma rectangular (de dimensiones: Lx, Ly y Lz), y se somete a un incremento uniforme de temperatura, el cambio de volumen vendrá dado por:
Aplicaciones
El conocimiento del coeficiente de dilatación (lineal) adquiere una gran técnica importancia en muchas áreas del diseño industrial. Un buen ejemplo son los rieles del ferrocarril, estos van soldados unos con otros por lo que pueden llegar a tener una longitud de varios centenares de metros. Si la temperatura aumenta mucho la vía férrea se desplazaría por efecto de la dilatación, deformando completamente el trazado. Para evitar esto, se estira el carril artificialmente, tantos centímetros como si fuese una dilatación natural y se corta el sobrante, para volver a soldarlo. A este proceso se le conoce como neutralización de tensiones.
Para ello, mediremos la temperatura media en la zona donde se instale la vía, le restaremos la que tengamos en ese momento en el carril, el resultado lo multiplicaremos por el coeficiente de dilatación del acero y por la longitud de la vía a neutralizar.
Valores del coeficiente de dilatación lineal

Algunos coeficientes de dilatación
| Material | α ( ° C-1 ) |
|---|---|
| Hormigón ~ | 1.0 x 10-5 |
| Hierro, acero | 1.2 x 10-5 |
| Plata | 2.0 x 10-5 |
| Oro | 1.5 x 10-5 |
| Invar | 0.04 x 10-5 |
| Plomo | 3.0 x 10-5 |
| Zinc | 2.6 x 10-5 |
| Aluminio | 2.4 x 10-5 |
| Latón | 1.8 x 10-5 |
| Cobre | 1.7 x 10-5 |
| Vidrio ~ | 0.7 x 10-5 |
| Cuarzo | 0.04 x 10-5 |
| Hielo | 5.1 x 10-5 |
Propiedades de los fluidos
Hidrostática
La Hidrostática es la rama de la Física que estudia los fluidos en estado de equilibrio. Los principales teoremas que respaldan el estudio de la hidrostática son el principio de Pascal y el principio de Arquímedes.
Presión hidrostática
La presión hidrostática es un tipo de presión debida al peso de un fluido en reposo, en éste la única presión existente es la presión hidrostática. En un fluido en movimiento además puede aparecer una presión hidrodinámica relacionada con la velocidad del fluido.
Un fluido pesa y ejerce presión sobre las paredes, sobre el fondo del recipiente que lo contiene y sobre la superficie de cualquier objeto sumergido en él. Esta presión, llamada presión hidrostática provoca, en fluidos en reposo, una fuerza perpendicular a las paredes del recipiente o a la superficie del objeto sumergido sin importar la orientación que adopten las caras. Si el líquido fluyera, las fuerzas resultantes de las presiones ya no serían necesariamente perpendiculares a las superficies.
Ecuación fundamental de la hidrostática

En el líquido en reposo, ver figura, se aísla un volumen infinitesimal, formado por un prisma rectangular de base y altura .
Considerese un plano de referencia horizontal a partir del cual se miden las alturas en el eje z.
La presión en la base inferior del prisma es , la presión en la base superior es . La ecuación del equilibrio en la dirección del eje z será:
o sea:
integrando esta última ecuación entre 1 y 2, considerando que se tiene:
o sea:
Considerando que 1 y 2 son dos puntos cualesquiera en el seno del líquido, se puede escribir la ecuación fundamental de la hidrostática del fluido incompresible en las tres formas que se muestran a continuación.
Ecuación fundamental de la hidrostática del fluido incompresible
Primera forma de la ecuación de la hidrostática
La ecuación arriba es válida para todo fluido ideal y real, con tal que sea incompresible.
(Fluido ideal es aquel fluido cuya viscosidad es nula)
Segunda forma de la ecuación de la hidrostática
La constante C2 se llama altura piezométrica
Tercera forma de la ecuación de la hidrostática
Donde:
- = densidad (física)|densidad del fluido
- = presión
- = aceleración de la gravedad
- = cota del punto considerado
Principio de Pascal
En física, el principio de Pascal o ley de Pascal, es una ley enunciada por el físico y matemático francés Blas Pascal (1623-1662) que se resume en la frase: «el incremento de presión aplicado a una superficie de un fluido incompresible, contenido en un recipiente indeformable, se transmite con el mismo valor a cada una de las partes del mismo».
El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el embolo, se observa que el agua sale por todos los agujeros con la misma presión.
Discusión
Una consecuencia del principio de Pascal es que el tensor tensión de un fluido incompresible en reposo dentro de un recipiente rígido, la parte del tensor tensión debida a las presiones aplicadas sobre su superficie viene dado por:
El tensor total, debido al peso del fluido hace que el fluido situado en la parte baja de un recipiente tenga una tensión ligeramente mayor que el fluido situado en la parte superior. De hecho si la única fuerza másica actuante es el peso del fluido, el estado tensional del fluido a una profundidad z el tensor tensión del fluido es:
En vista de lo anterior podemos afirmar que «fijado un punto de un fluido incompresible en reposo y contenido en un recipiente bajo presión e indeformable, la presión del fluido, es idéntica en todas direcciones».
Aplicaciones del principio
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter altamente incompresible de los líquidos. En esta clase de fluidos la densidad prácticamente constante, de modo que de acuerdo con la ecuación:
Donde:
, presión total a la profundidad .
, presión sobre la superficie libre del fluido.
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total (obviamente si el fluido fuera compresible, la densidad del fluido respondería a los cambios de presión y el principio de Pascal no podría cumplirse).
Prensa hidráulica

La prensa hidráulica es una máquina simple semejante a la palanca de Arquímedes, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.
La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección A1 se ejerce una fuerza F1 la presión p1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma instantánea a todo el resto del líquido; por tanto, será igual a la presión p2 que ejerce el líquido sobre el émbolo de mayor sección A2, es decir:
y por tanto:
Si la sección A2 es veinte veces mayor que la A1, la fuerza F1 aplicada sobre el émbolo pequeño se ve multiplicada por veinte en el émbolo grande.
Estabilidad de los cuerpos flotantes
Un cuerpo que flota en equilibrio en un fluido, se halla sometido a dos fuerzas: la fuerza de la gravedad, que puede considerarse aplicada en el centro de gravedad del objeto, y también al empuje hidrostático, cuantificable, según el principio de Arquímedes, por una fuerza igual al peso del líquido desalojado y que actúa en el centro de gravedad del volumen geométrico del líquido desalojado. Este último punto se denomina centro de empuje o carena.
Para que el cuerpo se encuentre en equilibrio es necesario que la suma de fuerzas y momentos se anulen. La anulación de las fuerzas se consigue al variar el grado de inmersión del cuerpo, lo que modifica el empuje.
Para la anulación de los momentos bastaría con que el centro de gravedad del cuerpo coincidiese con el de empuje. En caso contrario, el cuerpo se inclina, y si el centro de gravedad queda más abajo que el de empuje, el momento resultante tiende a recuperar la posición estable. Si no, el momento puede ser compensado por el creado por una fuerza exterior, como la fuerza del viento sobre un bote.
Hidrodinámica
- Principio de Bernouilli
- Teorema de Torricelli
- Tipos de regímenes
- Régimen ideal
- Consecuencias del teorema de Bernouilli
Tipos de regímenes
Física/Hidrodinámica/Tipos de regímenes
Régimen ideal
Física/Hidrodinámica/Régimen ideal
Teorema de Bernouilli
Física/Hidrodinámica/Teorema de Bernouilli
Consecuencias del teorema de Bernouilli
Física/Hidrodinámica/Consecuencias del teorema de Bernouilli
Teorema de Torricelli
Es una aplicación de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad. A partir del teorema de Torricelli se puede calcular el caudal de salida de un líquido por un orificio. "La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio": se puede calcular la velocidad de la salida de un liquido por un orificio
Donde:
- = velocidad teórica del líquido a la salida del orificio
- = velocidad de aproximación
- = distancia desde la superficie del líquido al centro del orificio
- = aceleración de la gravedad
En la práctica, para velocidades de aproximación bajas la expresión anterior se transforma en:
Donde:
- = velocidad del líquido a la salida del orificio
- = coeficiente que puede admitirse para cálculos preliminares, en aberturas de paredes delgadas, como 0.61
Fenómenos superficiales de los líquidos
- Fuerzas de cohesión
- Tensión superficial
- Capilaridad
- Influencia de la curvatura de la superficie
- Adherencia solido-liquido. Angulo de contacto
Fuerzas de cohesión
Fuerzas intermoleculares
Las fuerzas intermoleculares o Cohesión intermolecular son fuerzas electromagnéticas las cuales actúan entre moléculas o entre regiones ampliamente distantes de una macromolécula.
La cohesión es distinta de la adhesión; la cohesión es la fuerza de atracción entre partículas adyacentes dentro de un mismo cuerpo, mientras que la adhesión es la interacción entre las superficies de distintos cuerpos.
En los gases, la fuerza de cohesión puede observarse en su licuefacción, que tiene lugar al comprimir una serie de moléculas y producirse fuerzas de atracción suficientemente altas para proporcionar una estructura líquida.
En los líquidos, la cohesión se refleja en la tensión superficial, causada por una fuerza no equilibrada hacia el interior del líquido que actúa sobre las moléculas superficiales, y también en la transformación de un líquido en sólido cuando se comprimen las moléculas lo suficiente.
En los sólidos, la cohesión depende de cómo estén distribuidos los átomos, las moléculas y los iones, lo que a su vez depende del estado de equilibrio (o desequilibrio) de las partículas atómicas. Muchos compuestos orgánicos, por ejemplo, forman cristales moleculares, en los que los átomos están fuertemente unidos dentro de las moléculas, pero éstas se encuentran poco unidas entre sí.
Interreacciones iónicas
Son interacciones que ocurren a nivel de catión-anión, entre distintas moléculas cargadas, y que por lo mismo tenderán a formar una unión electrostática entre los extremos de cargas opuestas, lo que dependerá en gran medida de la electronegatividad de los elementos constitutivos. Un ejemplo claro de esto, es por ejemplo lo que ocurre entre los extremos Carboxilo y Amino de un amioacido, peptido, polipeptido u proteína con otra.
Fuerzas ion-dipolo
Estas son interacciones que ocurren entre especies con carga. Las cargas similares se repelen, mientras que las opuestas se atraen. Es la fuerza que existe entre un ion y una molécula polar neutra que posee un momento dipolar permanente, las moléculas polares son dipolos tienen un extremo positivo y un extremo negativo. Los iones positivos son atraídos al extremo negativo de un dipolo, en tanto que los iones negativos son atraídos al extremo positivo.
La magnitud de la energía de la interacción depende de la carga sobre el ion (Q), el momento dipolar del dipolo (µ), y de la distancia del centro del ion al punto medio del dipolo (d).
Las fuerzas ion-dipolo son importantes en las soluciones de las sustancias iónicas en líquidos.
Puente de Hidrógeno
El puente de hidrógeno ocurre cuando un átomo de hidrógeno es enlazado a un átomo fuertemente electronegativo como el nitrógeno, el oxígeno o el flúor. El átomo de hidrógeno posee una carga positiva parcial y puede interactuar con otros átomos electronegativos en otra molécula (nuevamente, con N, O o F). Asi mismo, se produce un cierto solapamiento entre el H y el átomo con que se enlaza (N,O o F) dado el pequeño tamaño de estas especies, siendo por tanto mayor el solapamiento cuanto menor sea el tamaño del átomo con que interacciona el H. Por otra parte, cuanto mayor sea la diferencia de electronegatividad entre el H y el átomo interactuante, más fuerte será el enlace. Fruto de estos presupuestos obtenemos un orden creciente de intensidad del enlace de hidrógeno: el formado con el F será de mayor intensidad que el formado con el O, y éste a su vez será más intenso que el formado con el N. Estos fenómenos resultan en una interacción estabilizante que mantiene ambas moléculas unidas. Un ejemplo claro del puente de hidrógeno es el agua:
Los enlaces de hidrógeno se encuentran en toda la naturaleza. Proveen al agua de sus propiedades particulares, las cuales permiten el desarrollo de la vida en la Tierra. Los enlaces de hidrógeno proveen también la fuerza intermolecular que mantiene unidas ambas hebras en una molécula de ADN.
Atracciones dipolo-dipolo
Las atracciones dipolo-dipolo, también conocidas como Keeson, por Willem Hendrik Keesom, quien produjo su primera descripción matemática en 1921, son las fuerzas que ocurren entre dos moléculas con dipolos permanentes. Estas funcionan de forma similar a las interacciones iónicas, pero son más débiles debido a que poseen solamente cargas parciales. Un ejemplo de esto puede ser visto en el ácido clorhídrico:
(+)(-) (+)(-) H-Cl----H-Cl (-)(+) (-)(+) Cl-H----Cl-H
Fuerza de Van der Waals
También conocidas como fuerzas de isperción, de London o fuerzas dipolo-transitivas, éstas involucran la atracción entre dipolos temporalmente inducidos en moléculas no polares. Esta polarización puede ser inducida tanto por una molécula polar o por la repulsión de nubes electrónicas con cargas negativas en moléculas no polares. Un ejemplo del primer caso es el cloro disuelto por que son puras puntas (-) (+)
[dipolo permanente] H-O-H----Cl-Cl [dipolo transitivo]
Un ejemplo del segundo caso se encuentra en la molécula de cloro:
(+) (-) (+) (-) [dipolo transitivo] Cl-Cl----Cl-Cl [dipolo transitivo]
Tensión superficial

[cuando uno esta enfermo .
La tensión superficial tiene como principal efecto la tendencia del líquido a disminuir en lo posible su superficie para un volumen dado, de aquí que un líquido en ausencia de gravedad adopte la forma esférica, que es la que tiene menor relación área/volumen.
Energéticamente, las moléculas situadas en la superficie tiene una mayor energía promedio que las situadas en el interior, por lo tanto la tendencia del sistema será a disminuir la energía total, y ello se logra disminuyendo el número de moléculas situadas en la superficie, de ahí la reducción de área hasta el mínimo posible.
Propiedades

La tensión superficial suele representarse mediante la letra γ. Sus unidades son de N·m-1=J·m-2.
Algunas propiedades de γ:
- γ > 0, ya que para aumentar el área del líquido en contacto hace falta llevar más moléculas a la superficie, con lo cual aumenta la energía del sistema y γ es , o la cantidad de trabajo necesario para llevar una molécula a la superficie.
- γ = 0 en el punto crítico, ya que las densidades del líquido y del vapor se igualan, por lo que según la Teoria del Gradiente de Densidades (DGT, en inglés) propuesta por van der Waals (1894),la tensión superficial en el punto crítico debe ser cero.
- γ depende de la naturaleza de las dos fases puestas en contacto que, en general, será un líquido y un sólido. Así, la tensión superficial será diferente por ejemplo para agua en contacto con su vapor, agua en contacto con un gas inerte o agua en contacto con un sólido, al cual podrá mojar o no debido a las diferencias entre las fuerzas cohesivas (dentro del líquido) y las adhesivas (líquido-superficie).
- γ se puede interpretar como un fuerza por unidad de longitud (se mide en N·m-1). Esto puede ilustrarse considerando un sistema bifásico confinado por un pistón móvil, en particular dos líquidos con distinta tensión superficial, como podría ser el agua y el hexano. En este caso el líquido con mayor tensión superficial (agua) tenderá a disminuir su superficie a costa de aumentar la del hexano, de menor tensión superficial, lo cual se traduce en una fuerza neta que mueve el pistón desde el hexano hacia el agua.
- El valor de γ depende de la magnitud de las fuerzas intermoleculares en el seno del líquido. De esta forma, cuanto mayor sean las fuerzas de cohesión del líquido, mayor será su tensión superficial. Podemos ilustrar este ejemplo considerando tres líquidos: hexano, agua y mercurio. En el caso del hexano, las fuerzas intermoleculares son de tipo fuerzas de Van der Waals. El agua, aparte de la de Van der Waals tiene interacciones de puente de hidrógeno, de mayor intensidad, y el mercurio está sometido al enlace metálico, la más intensa de las tres. Así, la γ de cada líquido crece del hexano al mercurio.
- Para un líquido dado, el valor de γ disminuye con la temperatura, debido al aumento de la agitación térmica, lo que redunda en una menor intensidad efectiva de las fuerzas intermoleculares. El valor de γ tiende a cero conforme la temperatura se aproxima a la temperatura crítica Tc del compuesto. En este punto, el líquido es indistinguible del vapor, formándose una fase continua donde no existe una superficie definida entre ambos.
Tensoactividad
Se denomina tensoactividad al fenómeno por el cual una sustancia reduce la tensión superficial al disolverse en agua u otra solución acuosa. Su fórmula es 2 Pi*D*Y = F; donde:
-D = Diámetro. -Y = Tensión Superficial -F = Fuerza
Influencia de la curvatura de la superficie
Derivación de la fórmula de Laplace

Si no actúan fuerzas normales a la superficie de un líquido, dicha superficie permanece plana. Sin embargo si la presión en ambos lados de la superficie difieren, aparacerá un fuerza normal a la superficie, que si ha de ser compensada por la tension superficial ocasiona la curvatura de la superfice. El diagrama muestra como la curvatura de un elemento diferencia de superficie produce una diferencia en las fuerzas de tensión superficial actuando sobre la misma. Cuando esta tensión superficial está compensada con la diferencia de presiones en ambos lados de la superficie se tiene que
donde es la tensión superficial. De este modo hemos derivido la conocida como fórmula de Laplace.
Aplicaciones
Una aplicación de la fórmula de Laplace es el caso de la formación de burbujas esféricas en el seno de un líquido. En este caso particular, la fórmula se reduce a
Puesto que para la formación de una burbuja sería necesario que se formase antes una cavidad muy pequeña, la diferencia de presión entre el interior de la burbuja y el líquido sería enorme, pues R debería ser muy pequeña, de ahí que las burbujas tiendan a formarse en cavidades previamente originadas, como las impurezas que lleve el líquido.
Adherencia solido-liquido. Angulo de contacto
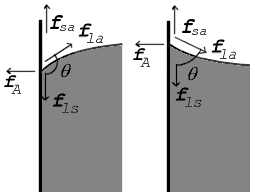 |
Las interacciones moleculares entre un sólido y un líquido hacen que en general el ángulo de contacto entre ellos no sea siempre el mismo. Dicho ángulo de contacto se define como el ángulo que forma la tangente de la superficie del líquido con la superficie sólida. Cuando las fuerzas de adherencia entre el sólido y el líquido son menores que las internas del líquido, en cuyo caso el ángulo de contacto es mayor de 90º y se dice que el líquido no moja. En caso contrario el ángulo de contacto es menor de 90º y se dice que el líquido moja.
Capilaridad
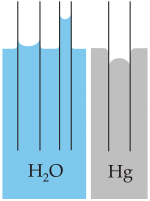
La capilaridad es la cualidad que posee una sustancia de absorber a otra. Sucede cuando las fuerzas intermoleculares adhesivas entre el líquido y el sólido son mayores que las fuerzas intermoleculares cohesivas del líquido. Esto causa que el menisco tenga una forma cóncava cuando el líquido está en contacto con una superficie vertical. En el caso del tubo delgado, éste succiona un líquido incluso en contra de la fuerza de gravedad. Este es el mismo efecto que causa que materiales porosos absorban líquidos.
Un aparato comúnmente empleado para demostrar la capilaridad es el tubo capilar; cuando la parte inferior de un tubo de vidrio se coloca verticalmente, en contacto con un líquido como el agua, se forma un menisco cóncavo; la tensión superficial succiona la columna líquida hacia arriba hasta que el peso del líquido sea suficiente para que la fuerza de la gravedad se equilibre con las fuerzas intermoleculares.
El peso de la columna líquida es proporcional al cuadrado del diámetro del tubo, por lo que un tubo angosto succionará el líquido más arriba que un tubo ancho. Así, un tubo de vidrio de 0,1 mm de diámetro levantará una columna de agua de 30 cm. Cuanto más pequeño es el diámetro del tubo capilar mayor será la presión capilar y la altura alcanzada. En capilares de 1 µm (micrómetro) de radio con una presión de succión 1,5*103hPa (hectopascal = hPa = 1,5atm), corresponde a una altura de columna de agua de 14 a 15 m.
Dos placas de vidrio que están separadas por una película de agua de 1 µm (micrómetro) de espesor, se mantienen unidas por una presión de succión de 1,5 atm. Por ello se rompen los portaobjetos humedecidos, cuando se trata de separalos.
Entre algunos materiales, como el mercurio y el vidrio, las fuerzas intermoleculares del líquido exceden a las existentes entre el líquido y el sólido, por lo que se forma un menisco convexo y la capilaridad trabaja en sentido inverso.
Las plantas usan la capilaridad para succionar agua a del entorno, aunque las plantas más grandes requieren la transpiración para mover la cantidad necesaria de agua allí donde se precise.
Ley de Jurin
La ley de Jurin define la altura que se alcanza cuando se equilibra el peso de la columna de líquido y la fuerza de ascensión por capilaridad.
La altura h en metros de una columna líquida está dada por:
donde:
- T = tensión superficial interfacial (N/m)
- θ = ángulo de contacto
- ρ = densidad del líquido (kg/m³)
- g = aceleración debido a la gravedad (m/s²)
- r = radio del tubo (m)
Para un tubo de vidrio en el aire a nivel del mar y lleno de agua,
- T = 0,0728 N/m a 20 °C
- θ = 20°
- ρ = 1000 kg/m³
- g = 9,80665 m/s²
entonces la altura de la columna está dada por:
- .
El estado gaseoso
- Modelo ideal de un gas
- Teoría cinético molecular de gases ideales
- Comprobaciones experimentales. Ley de Boyle-Mariotte
- Gases reales
Modelo ideal de un gas
El modelo más sencillo que podemos imaginar de un cuerpo macroscópico es el de un conjunto de masas puntuales que interaccionan entre ellas de forma instantánea cuando chocan. Las predicciones de este modelo concuerdan razonablemente bien con los experimentos con gases monoatómicos.
Las energías involucradas en los choques moleculares en las condiciones de laboratorio no son suficientes para alterar la energía interna de los átomos, pero sí para las de las moléculas. Este hecho explica por qué este modelo mínimo falla al aplicarlo a gases diatómicos.
Teoría cinético molecular de gases ideales
Concepto de presión

Si se considera un gas y una caja con un pistón que se puede desplazar en uno de sus extremos, siendo V el volumen de la caja, podemos imaginar las moléculas del interior golpeando el pistón con diferentes velocidades. Si en el exterior hay vacío y no se ejerce ninguna fuerza sobre el émbolo que compense el momento transferido al mismo por los choques moleculares, el pistón se verá empujado hacia afuera. La fuerza () que actúa sobre el émbolo será proporcional al número de choques, que a su vez es proporcional a su superficie (), por ello es conveniente trabajar con la fuerza por unidad de superficie que se define como presión.
Relación entre presión y trabajo
El trabajo diferencial () hecho sobre el gas al comprimirlo moviendo el pistón una cantidad diferencial () es el producto de la fuerza por la distancia y por tanto
donde se ha utilizado que el cambio diferencial de volumen es . El signo negativo concuerda con el convenio de considerar negativo el trabajo ejercido sobre el sistema.
Artículo: w:Criterio de signos termodinámico
Relación entre presión y energía
Para estimar la fuerza ejercida por el gas sobre el émbolo, supondremos que los choques de las moléculas con el mismo son perfectamente elásticas. Si no lo fuesen, el pistón comenzará a absorber energía y a calentarse, llegándose finalmente a un equilibrio térmico con el gas, momento en que por la segunda ley de la Termondinámica, el émbolo no podrá absorber más energía del gas. Así pues, en promedio, en cada choque la partícula incidente rebotará con la misma energía.
Sí es la velocidad de una molécula y la componente X de y el cambio de momento en el choque (considerado elástico) es . Si existen moléculas de gas en el volumen , la densidad atómica de partículas con velocidades entre y será . En un tiempo sólo golpearán el pistón la mitad de aquellas moléculas que estén a una distancia inferior a del pistón y como el área del émbolo es el número de colisiones es y el impulso se puede expresar entonces como
de lo que se puede deducir la presión
La presión para todas las velocidades v_x es
Desde el punto de vista del gas no hay nada especial en la dirección X por lo que
Podemos escribir la presión en función del promedio de la velocidad y no de su su componente X.
Obteniéndose una relación entre presión y energía cinética promedio del centro de masas de la molécula.
Para moléculas monoatómicas y si las energías involucradas no pueden excitar los átomos, se podrá considerar a los átomos como partículas puntuales y la energía cinética coincidirá con la energía total y la energía interna del gas () se puede calcular como el producto del número de átomos por la energía cinética promedio y por tanto
Relación entre presión y volumen con condiciones adiabáticas
Diferenciando en la relación entre presión y volumen para un gas monoatómico se llega a
y como
e integrando se llega a
Referencias
- Richard P. Feynman y Robert B. Leighton. Física. Volumen I: Mecánica, radiación y calor. 1987. México, D. F.: Sistemas Técnicos de Edición, S. A. de C. V. id = 968-858-091-0
Comprobaciones experimentales. Ley de Boyle
Física/El estado gaseoso/Comprobaciones experimentales. Ley de Boyle
Gases reales
Ecuación de van der Waals
La ecuación de estado del gas ideal no es del todo correcta: los gases reales no se comportan exactamente así. En algunos casos, la desviación puede ser muy grande. Por ejemplo, un gas ideal nunca podría convertirse en líquido o sólido por mucho que se enfriara o comprimiera. Por eso se han propuesto modificaciones de la ley de los gases ideales, pV = nRT. Una de ellas, muy conocida y particularmente útil, es la ecuación de estado de van der Waals
donde , y y son parámetros ajustables determinados a partir de medidas experimentales en gases reales. Son parámetros de la sustancia y no constantes universales, puesto que sus valores varían de un gas a otro. La ecuación de van der Waals también tiene una interpretación microscópica. Las moléculas interaccionan entre sí. La interacción es muy repulsiva a corta distancia, se hace ligeramente atractiva a distancias intermedias y desaparece a distancias más grandes. La ley de los gases ideales debe corregirse para considerar las fuerzas atractivas y repulsivas. Por ejemplo, la repulsión mutua entre moléculas tiene el efecto de excluir a las moléculas vecinas de una cierta zona alrededor de cada molécula. Así, una parte del espacio total deja de estar disponible para las moléculas en su movimiento aleatorio. En la ecuación de estado, se hace necesario restar este volumen de exclusión () del volumen del recipiente; de ahí el término .
Transiciones de fase
A temperaturas bajas (a las que el movimiento molecular se hace menor) y presiones altas o volúmenes reducidos (que disminuyen el espacio entre las moléculas), las moléculas de un gas pasan a ser influidas por la fuerza de atracción de las otras moléculas. Bajo determinadas condiciones críticas, todo el sistema entra en un estado ligado de alta densidad y adquiere una superficie límite. Esto implica la entrada en el estado líquido. El proceso se conoce como transición de fase o cambio de estado. La ecuación de van der Waals permite estas transiciones de fase, y también describe una región de coexistencia entre ambas fases que termina en un punto crítico, por encima del cual no existen diferencias físicas entre los estados gaseoso y líquido. Estos fenómenos coinciden con las observaciones experimentales. En la práctica se emplean ecuaciones más complejas que la ecuación de van der Waals.
La mejor comprensión de las propiedades de los gases ha llevado a la explotación a gran escala de los principios de la física, química e ingeniería en aplicaciones industriales y de consumo.
Difusión
Proceso físico

La difusión es un proceso físico irreversible, en el que partículas materiales se introducen en un medio que inicialmente estaba ausente de ellas aumentando la entropía del sistema conjunto formado por las partículas difundidas o soluto y el medio donde se difunden o disolvente.
Normalmente los procesos de difusión están sujetos a la Ley de Fick. La membrana permeable puede haber paso de partículas y disolvente, siempre también a favor del gradiente de concentración. La difusión, proceso que no requiere aporte energético es frecuente como forma de intercambio celular.
Ley de Fick
La ley de Fick es una ley cuantitativa en forma de ecuación diferencial que describe diversos casos de difusión de materia o energía en un medio en el que inicialmente no existe equilibrio químico o térmico. Recibe su nombre Adolf Fick, que las derivó en 1855.
En situaciones en las que existen gradientes de concentración de una sustancia, o de temperatura, se produce un flujo de partículas o de calor que tiende a homogeneizar la disolución y uniformizar la concentración o la temperatura. El flujo homogeneizador es una consecuencia estadística del movimiento azaroso de las partículas que da lugar al segundo principio de la termodinámica, conocido también como movimiento térmico casual de las partículas. Así los procesos físicos de difusión pueden ser vistos como procesos físicos o termodinámicos irreversibles.
Este flujo irá en el sentido opuesto de la gradiente y, si éste es débil, podrá aproximarse por el primer término de la serie de Taylor, resultando la ley de Fick
siendo el coeficiente de difusión de la especie de concentración .
En el caso particular del calor, la ley de Fick se conoce como ley de Fourier y se escribe como
siendo la conductividad térmica.
Combinando la ley de Fick con la ley de conservación para la especie c
resulta la ecuación de difusión o segunda ley de Fick:
Si existe producción o destrucción de la especie (por una reacción química), a esta ecuación debe añadirse un término de fuente en el segundo miembro.
Calorimetria
Calor, una forma de energía
Física/Calorimetria/Calor, una forma de energía
Capacidad calorífica
La capacidad calórica es la cantidad de calor que permite variar, en un grado, la temperatura de un cuerpo. Expresada en fórmula: donde: = capacidad calórica; = cantidad de calor; = variación de la temperatura.
El calor específico es la cantidad de calor cedido o absorbido por un gramo de una sustancia, para variar su temperatura en un grado Celsius. donde: = calor específico; = capacidad calórica; = masa
y el calor necesario para producir un cierto aumento de temperatura es
Significado molecular de la capacidad calorífica
El calor de una sustancia se expresa como cal/g y es la cantidad de calorias que una sustancia necesita para poder tener un estado de agregacion
Propagación del calor
Conducción térmica
Para que el calor pase o se transmita de un cuerpo a otro, se requiere que los mismos estén a diferentes temperaturas. Sean A y B dos fuentes que se hallan separadas, siendo sus temperaturas y ( mayor que ). El calor pasara desde A hacia B, hasta que se produzca el equilibrio térmico

Formas de propagación del calor
Conducción
Es una forma de transmisión del calor que se origina en sólidos, en los cuales la energía térmica (en forma de energía cinética) se propaga por vibración de molécula a molécula.
La expresión que rige la transmisión del calor en la unidad de tiempo por conducción en una pared plana o con un radio de curvatura mucho mayor que el espesor es
- ,
siendo:
- , el flujo de calor por unidad de tiempo;
- , el coeficiente de conductivilidad térmica, que depende del material;
- , el área de la barrera que permite la conducción térmica entre los sistemas;
- , el espesor de la pared;
- , la diferencia de temperaturas entre las caras de la pared....
Si el flujo de calor es a través de varias barreras, se puede generalizar la expresión para dar
Propagación por Convección
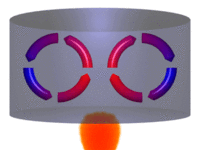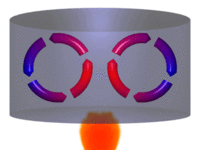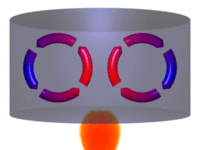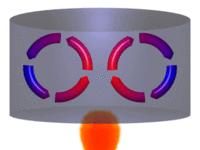
Es una forma de propagación del calor, se produce en los fluidos (líquidos y gases ) por un movimiento real de la materia. Este movimiento se origina por la disminución de la densidad de los fluidos con el aumento de temperatura (los hace mas livianos por unidad de volumen) que produce un ascenso de los mismos al ponerse en contacto con una superficie mas caliente y un descenso en el caso de ponerse en contacto con una superficie mas fría.
La expresión que rige la transmisión del calor por convección es
- ,
siendo
- , el flujo de calor por unidad de tiempo;
- , el coeficiente de transmisión de calor;
- , el área de contacto entre el fluido y la pared;
- es la diferencia de temperaturas entre el fluido y la cara de la pared en contacto con él.
Radiación
Todos los cuerpos irradian energía en forma de onda electromagnética , similares a las ondas de radio, rayos x , luz, etc. Lo único que difiere en estos distintos tipos de ondas es la longitud de onda o frecuencia.
El calor por radiación al igual que estas ondas se propaga a la velocidad de la luz (3·108 m/s en el vacío) y no necesita de un medio para poder propagarse. Se transmite a través del vacío mejor que a través del aire ya que este siempre absorbe parte de la energía.
La función que rige esta forma de propagación de la energía es la ley de Stefan – Boltzman
- ,
siendo
- , el flujo de calor por unidad de tiempo;
- , el área;
- , la emisividad de la superficie, que varía entre 0 y 1 (cuerpo negro);
- , la constante de Stefan–Boltzman, que vale ;
- es la temperatura absoluta del cuerpo
Todos los cuerpos irradian y reciben energía irradiada por otros cuerpos por lo tanto la energía neta irradiada es la diferencia entre la irradiada y la recibida la cuales se expresa (=
- ,
siendo
- la temperatura del cuerpo 1
- la temperatura del cuerpo 2
- el coeficiente de radiación mutua
Equilibrio térmico. Ley de las mezclas
Equilibrio térmico
Se dice que los cuerpos en contacto térmico se encuentran en equilibrio térmico cuando no existe flujo de calor de uno hacia el otro. Esta definición requiere además que las propiedades físicas del sistema, que varían con la temperatura, no cambien con el tiempo. Algunas propiedades físicas que varían con la temperatura son el volumen, la densidad y la presión.
El parámetro termodinámico que caracteriza el equilibrio térmico es la temperatura. Cuando dos cuerpos se encuentran en equilibrio térmico, entonces estos cuerpos tienen la misma temperatura.
Para poder dar una definición más precisa del concepto de equilibrio térmico desde un punto de vista termodinámico es necesario definir de forma más precisa algunos conceptos.
- Dos sistemas (entiéndase por sistema a una parte del universo físico) que están en contacto mecánico directo o separados mediante una superficie que permite la transferencia de calor (también llamada superficie diatérmica), se dice que están en contacto térmico.
Consideremos entonces dos sistemas en contacto térmico, dispuestos de tal forma que no puedan mezclarse o reaccionar químicamente. Consideremos además que estos sistemas están colocados en el interior de un recinto donde no es posible que intercambien calor con el exterior ni existan acciones desde el exterior capaces de ejercer trabajo sobre ellos. La experiencia indica que al cabo de un tiempo estos sistemas alcanzan un estado de equilibrio termodinámico que se denominará estado de equilibrio térmico recíproco o simplemente de equilibrio térmico.
El concepto de equilibrio térmico puede extenderse para hablar de un sistema o cuerpo en equilibrio térmico. Cuando dos porciones cualesquiera de un sistema se encuentran en equilibrio térmico se dice que el sistema mismo está en equilibrio térmico o que es térmicamente homogéneo. Experimentalmente se encuentra que, en un sistema en equilibrio térmico, la temperatura en cualquier punto del cuerpo es la misma.
Interpretación microscópica del equilibrio térmico
La Termodinámica proporciona una descripción macroscópica de los sistemas que estudia, sin hacer hipótesis acerca de la estructura microscópica de esos sistemas. Sin embargo, existen otras disciplinas, como la Mecánica Estadística, que estudian los mismos fenómenos que la Termodinámica, pero desde un enfoque microscópico.
En particular, el concepto de equilibrio térmico está ligado al concepto de temperatura al decir que dos sistemas en equilibrio térmico tienen la misma temperatura.
Desde un punto de vista microscópico, la temperatura esta asociada a la energía cinética promedio que tienen las partículas que constituyen el sistema, a saber, átomos, moléculas y/o la estructura electrónica de la sustancia que constituye el sistema.
Macroscópicamente, esta energía cinética promedio de las partículas de un sistema es lo que en la Termodinámica se llama energía interna, que es una energía que depende casi exclusivamente de la temperatura del sistema. A mayor energía cinética promedio de las partículas que constituyen un sistema, mayor energía interna y, en general, mayor temperatura del sistema.
La situación de dos sistemas en contacto térmico se interpreta microscópicamente como que las partículas de la superficie de interfase de ambos sistemas son capaces de interactuar entre sí.
Básicamente se puede ver que, microscópicamente, las partículas del sistema de mayor temperatura (que tienen mayor energía cinética) van a transferir parte de su energía a las partículas del otro sistema. Se encuentra que esta interacción entre los dos sistemas da lugar a que las partículas de los dos sistemas alcancen la misma energía cinética promedio y, por lo tanto, la misma temperatura. Es decir, desde un punto de vista microscópico, se entiende como equilibrio térmico entre dos sistemas que las partículas de los dos sistemas tengan la misma energía cinética promedio.
Desde un punto de vista macroscópico, se dice que los sistemas un estado de equilibrio, bajo las condiciones indicadas en la sección definición termodinámica del equilibrio térmico. En cambio, desde un punto de vista microscópico, el estado de equilibrio se refiere al promedio, ya que los dos sistemas continúan intercambiando energía incluso una vez alcanzado el equilibrio térmico. Sin embargo, la energía cinética individual de una partícula no es estacionaria, sino que es el promedio de la distribución de energías de todas las partículas del sistema lo que no cambia en el tiempo.
De igual manera que para el caso macroscópico, se puede extender el concepto de equilibrio térmico a un único sistema donde, en esa situación de equilibrio, las partículas de dos partes cualesquiera del sistema tienen la misma energía cinética promedio.
Ley de las mezclas
Al mezclar agua caliente y agua fría el resultado es agua tibia, debido a que el agua caliente cede una determinada cantidad de calor que es absorbida por el agua fría.
Esta situación es una manifestación del principio de las mezclas calóricas
|
Si dos o más cuerpos de diferentes temperaturas se mezclan, el calor absorbido por los cuerpos fríos equivale al calor cedido por los cuerpos calientes, quedando todos a una temperatura común |
Ley cero de la termodinámica
El concepto de equilibrio térmico es la base de la llamada Ley Cero de la Termodinámica. Esta ley proposición fue enunciada por R. H. Fowler en 1931. La ley cero de la termodinámica se enuncia diciendo:
|
La experiencia indica que si dos sistemas A y B se encuentran, cada uno por separado, en equilibrio térmico con un tercer sistema, que llamaremos C, entonces A y B se encuentran en equilibrio térmico entre sí. |
Termodinámica
- Introducción a la termodinámica
- Estado termodinámico
- Transferencia de calor
- Ley cero de la termodinámica y temperatura empírica
- Ecuación de estado
- Proceso termodinámico
- Criterio de signos
- Trabajo ejercido por un gas
Estado termodinámico
Ecuación de estado
Ecuación de Estado
En el capítulo anterior hemos definido el conjunto de todos los estados de equilibrio (estados termodinámicos) de un sistema termodinámico real. También hemos definido lo que es un sistema de coordenadas, formado por un número de variables termodinámicas. En este contexto, la ecuación de estado es una relación entre las variables termodinámicas que forman el sistema de coordenadas que determina el conjunto de puntos (en el sistema de coordenadas) que corresponden a estados del sistema con la misma temperatura empírica.
Lema. Para todo fluido es posible encontrar una función de ciertas variables independientes por ejemplo , en la cual el valor numérico de dicha función es el mismo para todos los fluidos que están en equilibrio entre sí. Al valor numérico se le llama temperatura empírica y a la ecuación.
se llama ecuación de estado del sistema. En palabras más simples la ecuación de estado es un mapeo inyectivo del experimento al sistema de coordenadas termodinámicas. Es decir que para cada estado real del gas existe un único punto con lo que podemos determinar el estado real del sistema por medio de dicha función. Todo esto quiere decir que podemos conocer el estado de un sistema en todo momento si variamos cuasi-estáticamente uno de los grados de libertad del sistema termodinámico.
Si en general para describir el sistema se requieren de variables independientes se puede escribir
Tomando solo dos variables por ejemplo , y por consecuencia de la Ley Cero de la termodinámica podemos hacer la siguiente relación
por lo cual también podemos escribir dicha ecuación de estado en términos de
Ahora consideramos un proceso cuasi-estático (en donde todos los estados intermedios son estados de equilibrio del sistema) y para cada uno existe una ecuación de estado de acuerdo con lo que formulamos antes, aplicamos una pequeña variación a por donde , pero lo suficientemente grande para que su valor no sea afectado por las influencia entre las partículas. Matemáticamente, podemos describir este pequeño cambio calculando la diferencial total
Esta ecuación describe el incremento en cuando las variables independientes y sufren un incremento , . Analogicamente existen dos ecuaciones para y para que se obtiene considerando el incremento en las variables independientes respectivas, éstas son
Lo que queremos hacer notar con esto es que a partir de estas 3 ecuaciones podemos calcular todas las propiedades del sistema termodinámico sin conocer la forma analítica de la ecuación de estado.
Deducción de la Ecuación del Gas ideal
Si tomamos por ejemplo como la presión de un gas dentro de un pistón y como el volumen del pistón la ecuación para un gas ideal toma la forma más sencilla. Se hacen experimento con dicho pistón variando por ejemplo el volumen y dejando (la presión en función del volumen); al disminuir el volumen se observa que la presión aumenta por lo que deducimos que la gráfica es decreciente, lo nos hace pensar que su derivada es negativa. Ahora tomando como variable la temperatura y observamos que entre mayor calor le apliquemos al pistón la presión aumentará por lo que la gráfica de esta es creciente por lo que su derivada es positiva.
Tomando lo anterior la diferencial total de la presión (por ejemplo) quedaría de la siguiente manera
Suponiendo el caso más sencillo de la ecuación anterior en donde el gradiente no hay variación tenemos la siguiente expresión
integrando
por lo que
donde es una constante, la cual es determinada por el producto de la masa del gas y la constante universal de los gases .
La constante universal de los gases se a calculado experimentado con varios gases como , , , , etc. efectuando mediciones de p y V a diferentes temperaturas y graficando los resultados en un diagrama donde es el eje ordenado y el de la abscisas. Lo que concluye fue que todas las isotermas intersectan el eje ordenado en el mismo punto, independientemente de la naturaleza del gas, por lo que la constante universal de los gases se definió de la siguiente manera
Obteniendo por fin la ecuación de estado de un gas ideal
donde
p presión
V volumen
n masa molar
R constante universal de los gases
T temperatura
Pero esta no es la única ecuación de estado, de hecho podemos construir una ecuación de estado un poco más precisa, considerando esta vez el volumen del gas y la atracción entre partículas . Esto fue lo que hizo Johannes van der Waals en el siglo XIX y propuso la siguiente fórmula para describir el estado de un gas
n número de moles.
a Medida para la atracción entre partículas.
b Volumen excluido por mol.
La anterior es llamada ecuación de estado para un gas de van der Waals en donde hay que hacer notar que si las constantes y son cero el resultado es la ecuación de estado para el gas ideal.
Proceso termodinámica
Física/Termodinámica/Proceso termodinámica
Criterio de signos
Física/Termodinámica/Criterio de signos
Trabajo ejercido por un gas
Trabajo ejercido por un gas
Consideramos el trabajo ejercido por un gas a lo largo de un proceso cuasi-estático. Supongamos un gas encerrado en un contenedor rígido el cual sólo tenga una pared movible (pistón). El estado del gas encerrado está determinado por las variables (presión, volumen), y (temperatura). La pared movible experimenta la fuerza debido a la presión del gas (A es el área de la sección trasversal del pistón).
Para que el proceso pueda ser cuasi-estático esta fuerza debe ser compensada por una fuerza contraria, aplicada por algún dispositivo externo. Para conducir el proceso hay que disminuir y luego controlar esta fuerza compensatoria con mucho cuidado de tal forma que la pared se mueve lentamente de la posición inicial a la posición final . El trabajo que ejerce el gas está definido como el negativo del producto de la fuerza que tiene que vencer y la distancia que recorre la pared. En nuestro caso
Para geometrías arbitrarias, esta formula toma la forma
Como podemos ver, es positivo cuando el gas ejerce trabajo (expandiéndose), mientras que es negativo cuando los alrededores ejercen trabajo en el sistema (comprimiendo el gas). En un sistema de coordenadas donde se marca en la abscisa y en la ordenada (plano ), el trabajo es igual al área bajo la curva , que representa el proceso en consideración.
|
Ejemplo Tomamos como ejemplo la expansión isotérmica de moles de un gas. Para poder calcular el trabajo ejercido por el gas durante este proceso, se necesita conocer la ecuación de estado del gas. Supongamos un gas ideal con la ecuación de estado , donde es la constante universal de los gases ideales y es la temperatura en Kelvin. Si el gas se expande de un volumen a un volumen , se obtiene: |
Primer principio de la termodinámica
Física/Termodinámica/Primer principio de la termodinámica
Segundo principio de la termodinámica
Física/Termodinámica/Segundo principio de la termodinámica
Maquinas reversibles
Física/Termodinámica/Maquinas reversibles
Entropía de un proceso irreversible
Física/Termodinámica/Entropía de un proceso irreversible
Tercer principio de la termodinámica
Física/Termodinámica/Tercer principio de la termodinámica
Superficies
Física/Termodinámica/Superficies
Cambios de fase principal
Física/Termodinámica/Cambios de fase principal
Presión y temperatura de cambio de fase
Física/Termodinámica/Presión y temperatura de cambio de fase
Gases y vapores. Punto critico
Física/Termodinámica/Gases y vapores. Punto critico
Aplicaciones de la termodinámica
- Introducción a la termodinámica
- Estado termodinámico
- Transferencia de calor
- Ley cero de la termodinámica y temperatura empírica
- Ecuación de estado
- Proceso termodinámico
- Criterio de signos
- Trabajo ejercido por un gas
Maquinas térmicas
Física/Termodinámica/Maquinas térmicas
Motores
Maquinas frigoríficas
Física/Termodinámica/Maquinas frigoríficas
Electromagnetismo
- Historia del Electromagnetismo
- Electrización por inducción
- Electroscopio
- Estructura de la materia
- Fuerzas entre cargas
- Campo eléctrico
- Generalidades Campo eléctrico
- Intensidad de campo
- Potencial
- Líneas de fuerza
- Potencial e intensidad de un punto de un campo radial
- Distribución de la carga en un conductor en equilibrio
- Generador de Van der Graaff
- Electrodinámica
- Ondas electromagnéticas
- Circuito oscilante
- Ondas electromagnéticas
- Gama de ondas electromagnéticas
- Propiedades de las ondas electromagnéticas
Electricidad. Electrostática
- Historia del Electromagnetismo
- Electrización por inducción
- Electroscopio
- Estructura de la materia
- Fuerzas entre cargas
- Campo eléctrico
- Generalidades Campo eléctrico
- Intensidad de campo
- Potencial
- Líneas de fuerza
- Potencial e intensidad de un punto de un campo radial
- Distribución de la carga en un conductor en equilibrio
- Generador de Van der Graaff
- Electrodinámica
- Ondas electromagnéticas
- Circuito oscilante
- Ondas electromagnéticas
- Gama de ondas electromagnéticas
- Propiedades de las ondas electromagnéticas
Electrizaron por frotamiento
Física/Electromagnetismo/Electrizaron por frotamiento
Electrizaron por contacto
Física/Electromagnetismo/Electrizaron por contacto
Clases de electricidad
Estática
Son cargas que no se mueven. Se crea por la frotación de un objeto sobre otro. Por ejemplo, cuando nos peinamos se produce electricidad estática.
Dinámica
Es el flujo o movimiento continuo de cargas eléctricas, para ellos se emplean materiales que permiten que las cargas se muevan con mayor facilidad como el cobre. Esta electricidad se produce de muchas maneras.
-Reacción química
Se emplean en las pilas para almacenar y transmitir electricidad.
-Solar
Se produce por el efecto de los rayos del sol en celdas fotovoltaicas.
-Inducción electromagnética
Se produce a través del movimiento de imanes en motores especiales.
La energía eléctrica por la acción mecánica de un agente. Ejemplo de ello es la que genera la acción del agua (energía hidroeléctrica) y el aire (energía eólica).
Fuentes
http://bitacora.rena.edu.ve/estudios-de-la-nauraleza/
http://www.rena.edu.ve/SegundaEtapa/tecnologia/laelectricidad.html
Electrizaron por inducción
Física/Electromagnetismo/Electrizaron por inducción
Electroscopio
Descripción

El electroscopio es un instrumento que permite determinar la presencia de cargas eléctricas.
Un electroscopio sencillo consiste en una varilla metálica vertical que tiene una bolita en la parte superior y en el extremo opuesto dos láminas de oro muy delgadas. La varilla está sostenida en la parte superior de una caja de vidrio transparente con un armazón de metal en contacto con tierra. Al acercar un objeto electrizado a la esfera, la varilla se electrifica y las laminillas cargadas con igual signo que el objeto se repelen, siendo su divergencia una medida de la cantidad de carga que han recibido. La fuerza de repulsión electrostática se equilibra con el peso de las hojas. Si se aleja el objeto de la esfera, las láminas, al perder la polarización, vuelven a su posición normal.
Cuando un electroscopio se carga con un signo conocido, puede determinarse el tipo de carga eléctrica de un objeto aproximándolo a la esfera. Si las laminillas se separan significa que el objeto está cargado con el mismo tipo de carga que el electroscopio. De lo contrario, si se juntan, el objeto y el electroscopio tienen signos opuestos.
Un electroscopio cargado pierde gradualmente su carga debido a la conductividad eléctrica del aire producida por su contenido en iones. Por ello la velocidad con la que se carga un electroscopio en presencia de un campo eléctrico o se descarga puede ser utilizada para medir la densidad de Iones en el aire ambiente. Por este motivo, el electroscopio se puede utilizar para medir la radiación de fondo en presencia de materiales radiactivos.
El primer electroscopio fue creado por el médico inglés William Gilbert para realizar sus experimentos con cargas electrostáticas. Actualmente este instrumento no es más que una curiosidad de museo, dando paso a mejores instrumentos electrónicos.
Materiales
Tiras de Hojalata o chapa galvanizada: Recorte una tira de hojalata de 5cm de ancho por 26cm de largo, otra del mismo ancho y 12cm de largo, y una tercera de 4cm de ancho por 8cm de largo. Tornillo de 4cm de largo y cabeza fresada Tres tuercas que hagan juego Gajo de PVC de 5cm de ancho y 10cm de largo tomado de un caño para cloacas Seis remaches pop cortos Hojuela fija
Corte en hojalata un rectángulo de 11 x 2 cm
Marque las líneas divisorias AB y CD
Practique la perforación mostrada, por donde pasará el tornillo
Marque y recorte con cuidado la ventana central, de modo que sus bordes no presenten irregularidades.
Doble la pieza a 90 grados por la línea CD
Doble la pieza por la línea AB, y conforme una media caña de unos 3 milímetros, donde apoyará la hojuela móvil
Hojuela móvil: Recórtela en papel obra (de una hoja de cuaderno) de acuerdo a las medidas indicadas:
Determinación de la carga a partir del ángulo de separación de las láminas

Un modelo simplificado de electroscopio consiste en dos pequeñas esferas de masa m cargadas con cargas iguales q y del mismo signo que cuelgan de dos hilos de longitud l, tal como se indica la figura. A partir de la medida del ángulo que forma una esfera con la vertical, se puede calcular su carga q.
Sobre cada esfera actúan tres fuerzas: el peso mg, la tensión de la cuerda T y la fuerza de repulsión eléctrica entre las bolitas F.
En el equilibrio: (1) y (2).
Dividiendo (1) entre (2) miembro a miembro, se obtiene:
Midiendo el ángulo θ se obtiene, a partir de la fórmula anterior, la fuerza de repulsión F entre las dos esferas cargadas.
Según la Ley de Coulomb: y como y
Entonces, como se conoce y ha sido calculado, despejando se obtiene IDENTIFICACIÓN DEL APARATO
Determinación del ángulo de separación de las láminas a partir de la carga
Como muestra el apartado anterior se cumple:
con lo cual:
Teniendo en cuenta que y operando apropiadamente, se obtiene:
siendo y
Ésta es una Ecuación de tercer grado que no tiene una solución analítica fácil. Posee una raíz que se puede calcular aplicando un procedimiento numérico.
Con determinaciones de este tipo se puede dibujar una curva que muestre el comportamiento del electroscopio, en la cual, leyendo en el eje de las abscisas el valor de , se puede obtener el valor de en el eje de las ordenadas.
Estructura de la materia
Estructura de la materia
La materia consiste de partículas extremadamente pequeñas agrupadas juntas para formar el átomo. Hay una 90 ocurrencias naturales de estas agrupaciones de partículas llamadas elementos.
Estos elementos fueron agrupados en la tabla periódica de los elementos en secuencia de acuerdo a sus números atómicos y peso atómico. Hay además 23 elementos hechos por el hombre que no ocurren en la naturaleza, por lo que al final son unos 113 elementos conocidos hasta la fecha. Estos elementos no pueden cambiarse por procesos químicos. Ellos solo pueden ser cambiados por reacción nuclear o atómica, sin embargo pueden ser combinados para producir el incontable número de compuestos con los que tropezamos día a día.
Estructura del átomo
Un átomo puede ser representado simbólicamente en un modelo que recrea nuestro sistema solar, el cual tiene en el centro el sol y los planetas girando en órbitas alrededor de él.
Este modelo atómico, representado en la figura 1 fue propuesto por el físico Danés, Niels Bohr en 1913. Los mecanismos cuánticos actuales han demostrado que este modelo no es exactamente correcto, pero sigue siendo útil para la visualización de átomo.
El centro del átomo se llama núcleo y está principalmente formado por las partículas llamadas Protones y Neutrones, los que constituyen la mayoría de la masa del átomo. Orbitando alrededor del los núcleos están pequeñas partículas llamadas electrones. Estos electrones tienen una masa muchas veces mas pequeña que el Protón y el Neutrón. Hay otras partículas sub-atómicas estudiadas por los físicos atómicos, pero estas tres son suficientes para nuestro propósito.

Todos los elementos de la tabla periódica están formados por las tres partículas con la sola excepción del Hidrógeno que tiene un núcleo formado por un protón simple, alrededor del cual gira orbitando un electrón. El protón y el neutrón tienen una masa de alrededor de 1840 veces la masa del electrón.
Número y peso atómicos
Los elementos se identifican por su número y masa atómicos. Normalmente, un átomo tiene igual número de protones en su núcleo que de electrones girando alrededor de él. El número de protones del núcleo constituye el número atómico del elemento. De manera simplificada la masa atómica de un elemento es numéricamente igual al total de partículas mayores (protones y neutrones) en el núcleo.
Uno de los primeros elementos estudiados por los científicos fue el oxígeno. Después de la investigación, en el núcleo del oxígeno se encontraron 8 protones y 8 neutrones, por lo que le fueron asignados 16 como peso atómico y 8 como número atómico.
Niveles y sub-niveles
Como se muestra en la figura 2 los electrones que giran alrededor del núcleo los hacen agrupados en anillos u órbitas. Esas órbitas se tratan como niveles de energía los que a su vez contienen además sub-niveles. Cada nivel y sub-nivel de energía dependiendo de la distancia al núcleo contiene un cierto número máximo de electrones que no puede excederse. El primer nivel puede tener 2 electrones, el segundo 8 (2 en el primer sub-nivel y 6 en el segundo), el tercero puede contener 18 (2, 6, 10), el cuarto puede contener 32 (2, 6, 10, 14), etc.
figura2
Figura 2. El último nivel de energía de un átomo se llama nivel de valencia y puede estar lleno con el número máximo de electrones permitidos o tener electrones en defecto.
Como este último nivel de energía está incompleto puede aceptar o ceder alguno de los electrones a otro átomo de otro elemento que cumpla la misma condición y así formar uniones de átomos diferentes que comparten uno o mas electrones. Este enlace de átomos constituye la base de la comprensión de las reacciones químicas para formar sustancias complejas a partir de elementos simples. Cuando el último nivel está completo el átomo no puede compartir electrones siendo una sustancia muy estable y que no forma compuestos con otros elementos en condiciones normales, estas sustancias son los llamados gases nobles, Helio Argón Xenón etc.
La figura 3 representa el elemento aluminio, en el gráfico puede observarse que tiene tres electrones en el último nivel, estos electrones pueden ser compartidos con otro elemento por lo que la valencia del aluminio es 3.
figura3
Figura 3.
Carga eléctrica
Los protones y electrones ejercen fuerzas mutuas entre ellos, mas o menos como si existiera una fuerza gravitacional entre ellos, por lo que se ha supuesto que las masas de estas partículas son portadoras de cierta carga eléctrica y que la fuerza de interacción entre ellas es entonces una fuerza eléctrica.
En la práctica estas fuerza eléctricas son de atracción entre partículas de naturaleza diferente (protones y electrones) y de repulsión entre las partículas de la misma naturaleza al igual que los polos de un imán, esto hace pensar en cargas de diferente naturaleza las que han sido convencionalmente denominadas positiva (+) para el protón y negativa (-) para el electrón.
Se ha demostrado además que la magnitud de las cargas de las partículas con independencia de la enorme diferencia de masa son iguales, por lo que el átomo normal (misma cantidad de protones y electrones) es una entidad neutra eléctricamente hablando. Esta carga de las partículas elementales es la menor cantidad de carga eléctrica que puede existir por lo que se ha convenido en denominar carga elemental.
Fuentes
http://www.sabelotodo.org/materia/materia.html
http://www.eis.uva.es/~qgintro/atom/tutorial-02.html
Fuerzas entre cargas
De los experimentos con los cuerpos electrizados se deducen una serie de hechos:
- Los cuerpos electrizados interaccionan unos con otros, ejerciendo entre ellos fuerzas.
- En algunas ocasiones estas fuerzas son de atracción y en otras ocasiones son de repulsión.
De estos hechos se deduce que los cuerpos electrizados adquieren una propiedad que se ha dado en llamar carga eléctrica y de la que existen dos manifestaciones que convencionalmente se les asignó la cualidad positiva y negativa.
Los cuerpos cuya carga eléctrica es diferente se atraen, caso contrario se repelen. Este hecho es nombrado a veces como la parte cualitativa de la ley de coulomb.
Esta repulsión y atracción es mutua, es decir, cumple con la tercera ley de newton.
Ley de coulomb
La fuerza originada entre dos cargas son dos vectores, uno para cada cuerpo, de igual módulo pero de direcciones contrarias.
Su módulo es directamente proporcional a las cargas e inversamente proporcional a la distancia.
La constante que las relaciona (K) tiene un valor de 82978 . 10 9 Nm2/C2, pero es redondeada en algunas aplicaciones a 9. 10 9Nm2/C2.
Entonces la ley de coulomb queda de esta forma, para hayar el modulo de la fuerza entre las cargas:
Donde q1 y q2 son los valores absolutos de las cargas de las partículas.
Fuerza en otro medio.
La relación anterior es en el vacío donde la permitividad termica (epsilon) es 1. En otro medio se tiene que tener en cuenta la permitividad eléctrica, que varía con el medio.
De esta forma:
Además como la permitividad en el aire es aproximadamente 1, la fuerza en el vacío y en el aire solo tiene una ligera variación.
También es de resaltar que mencionada permitividad eléctrica es en lo mínimo 1, por lo que la mayor fuerza de atracción será cuando los cuerpos estén en el vacío.
Formulación vectorial de la Ley de Coulomb
La Fuerza entre cargas eléctricas se puede formular matemáticamente usando el formalismo de vectores de la siguiente manera:
Donde es el vector que une la posición de q1 con la posición de q2
Campo eléctrico
- Historia del Electromagnetismo
- Electrización por inducción
- Electroscopio
- Estructura de la materia
- Fuerzas entre cargas
- Campo eléctrico
- Generalidades Campo eléctrico
- Intensidad de campo
- Potencial
- Líneas de fuerza
- Potencial e intensidad de un punto de un campo radial
- Distribución de la carga en un conductor en equilibrio
- Generador de Van der Graaff
- Electrodinámica
- Ondas electromagnéticas
- Circuito oscilante
- Ondas electromagnéticas
- Gama de ondas electromagnéticas
- Propiedades de las ondas electromagnéticas
Generalidades
Historia
En el año 1820, Oersted descubrió que una corriente eléctrica origina un campo magnético a su alrededor, lo que constituyó un hecho clave para el desarrollo de dispositivos de conversión electromecánica de la energía. En efecto, como es sabido, la presencia del campo magnético es imprescindible para la conversión de energía eléctrica en energía mecánica y viceversa: En un motor, la energía eléctrica (corriente) crea un campo de fuerza (campo magnético) bajo el cual otro elemento de corriente produce una fuerza que, bajo ciertas condiciones, genera movimiento (energía mecánica). En un generador, la variación en el tiempo de la geometría de un circuito magnético (energía mecánica) produce una variación en el tiempo del flujo magnético que induce voltajes en los circuitos eléctricos que lo enlazan (energía eléctrica). Siendo fundamental en ambos casos la presencia del campo magnético, se estudiara éste con algún detalle.
Generalidades de un campo eléctrico
Un Campo Eléctrico tiene como características principales la dirección, el sentido y la intensidad,
Duración y Sentido de un Campo Eléctrico
La Dirección y Sentido de un Campo Eléctrico en un punto se define como la dirección y sentido de la fuerza que se ejercería sobre una carga puntual y positiva (carga de prueba q) situada en dicho punto.
Un Campo Eléctrico puede representarse por líneas de fuerza, líneas que son tangentes a la dirección del campo en cada uno de sus puntos.
Líneas de fuerza de un campo eléctrico
Un campo eléctrico se puede representar como líneas de Fuerza (no existen en realidad) y son útiles para el estudio del mismo. Ver el siguiente diagrama
Las líneas de fuerza indican en cada punto la dirección que tiene el campo eléctrico (E). Estas líneas nunca se cruzan entre sí, y mientras más cercanas estén significa que el campo eléctrico es más intenso. Sin embargo hay que tomar en cuenta de que para un campo eléctrico determinado el número de líneas de fuerza es el mismo Las líneas de fuerza de un campo eléctrico siempre inician en la carga positiva y terminan en la carga negativa.
http://lfushion.blogspot.mx/2009/06/cuando-en-una-region-del-espacio-una.html
https://www.u-cursos.cl/ingenieria/2010/1/EL42C/1/material_docente/previsualizar?id_material=276002
Intensidad de campo
Se denomina intensidad del campo eléctrico en un punto a la fuerza que sufriría una carga puntual de +1 Culombio situada en ese punto, matemáticamente y para el campo creado por una carga puntual:
Potencial
Trabajo de desplazamiento de una carga en un campo eléctrico
Supongamos que tenemos una carga puntual de +q1 culombios. En las cercanías de esa carga colocamos una carga de q2 culombios y queremos desplazarla de un punto A a un punto B, siguiendo una determinado camino.
Para ello hemos de realizar un trabajo a favor o en contra de las fuerzas del campo creado por la carga q1.
El trabajo infinitesimal realizado para llevar a la carga q desde un punto a otro situado en será:
|
|
En principio el trabajo realizado dependerá de la trayectoria que se recorra para ir del punto inicial al punto final, pero por las características del campo queda demostrado que el trabajo solo va depender de la distancia radial a la que estén los puntos inicial y final, es decir no importa como se llegue del punto A al punto B, el trabajo realizado solo dependerá de la distancia al origen del campo (la carga q1), es decir de cual es el punto de inicio y cual es el punto de llegada.
El trabajo para trasladar la carga del punto A al punto B solo dependerá de la distancia r:
|
|
Energía potencial de una carga en un campo creado por una carga puntual
De la exposición del apartado anterior podemos definir una función que solo depende de la distancia al origen del campo, y cuyo variación no depende de la trayectoria de desplazamiento de las cargas sino solo del punto inicial y final.
Es importante resaltar el hecho de que la variación de la función energía potencial del campo no depende del camino seguido por la carga eléctrica al desplazarse desde el primer punto al segundo punto. Es decir que la función energía potencial solo depende de la posición de la carga en el campo eléctrico o sea de la distancia a la fuente del campo.
Los campos de fuerza que cumplen esta condición se les denomina conservativos.
La función Energía pontencial eléctrica quedaría definida para cada punto calculando el trabajo realizado para desplazar la carga eléctrica desde un punto donde la fuerza electrostática fuera cero (matemáticamente sería en el infinito) llamado "infinito del campo" hasta el punto donde se quiere calcular la energía potencial.
|
|
El último término tiende a cero, con lo que nos queda:
|
|
Este trabajo lo podemos calcular como si fuera la variación de una función U, llamada energía potencial eléctrica desde el infinito del campo hasta el punto donde se quiere evaluar la energía potencial:
|
|
puesto que el valor de la energía potencial eléctrica en el infinito del campo es nulo.
Así definida la función energía potencial eléctrica sería:
|
|
Esta función sería físicamente el trabajo de una fuerza que habría que hacer contra el campo creado por una carga q1 para desplazar una carga q2 desde un lugar donde la fuerza eléctríca entre las dos cargas fuera nula (infinito del campo) hasta una posición dentro del campo a una distancia r de la carga q1.
La clave, la fuerza para desplazar la carga a velocidad constante, ha de ser igual en magnitud y de sentido contrario a la fuerza eléctrica, de modo que si las dos cargas son del mismo signo hay que hacer fuerza para acercar las cargas, pero si las cargas son de distinto signo, hay que hacer fuerza para frenar la carga.
En el caso de que las cargas sean del mismo signo, la energía potencial es positiva, es decir, aumenta al acercar las dos cargas.
En el caso de que las cargas sean de distinto signo, la energía potencial es negativa, es decir, disminuye al acercar las dos cargas.
Líneas de fuerza
Representación del campo eléctrico.Líneas de fuerza del campo eléctrico
Flujo del campo eléctrico
Teorema de Gauss
Potencial e intensidad de un punto de un campo radial
El potencial eléctrico o potencial electrostático en un punto, es el trabajo que debe realizar un campo electrostático para mover una carga positiva desde dicho punto hasta el punto de referencia,[1] dividido por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga positiva unitaria q desde el punto de referencia hasta el punto considerado en contra de la fuerza eléctrica a velocidad constante. Matemáticamente se expresa por:
El potencial eléctrico sólo se puede definir unívocamente para un campo estático producido por cargas que ocupan una región finita del espacio. Para cargas en movimiento debe recurrirse a los potenciales de Liénard-Wiechert para representar un campo electromagnético que además incorpore el efecto de retardo, ya que las perturbaciones del campo eléctrico no se pueden propagar más rápido que la velocidad de la luz.
Si se considera que las cargas están fuera de dicho campo, la carga no cuenta con energía y el potencial eléctrico equivale al trabajo necesario para llevar la carga desde el exterior del campo hasta el punto considerado. La unidad del Sistema Internacional es el voltio (V).
Todos los puntos de un campo eléctrico que tienen el mismo potencial forman una superficie equipotencial. Una forma alternativa de ver al potencial eléctrico es que a diferencia de la energía potencial eléctrica o electrostática, él caracteriza sólo una región del espacio sin tomar en cuenta la carga que se coloca ahí.
Potencial debido a una carga puntual
Considérense los puntos A y B y una carga puntual q tal como muestra la figura. Según se muestra, apunta a la derecha y , que siempre está en la dirección del movimiento, apunta a la izquierda. Por consiguiente:
Ahora bien, al moverse la carga una trayectoria dl hacia la izquierda, lo hace en la dirección de la r decreciente porque r se mide a partir de q como origen. Así pues:
Por lo cual:
Combinando esta expresión con la de E para una carga puntual se obtiene:
Escogiendo el punto de referencia A en el infinito, esto es, haciendo que , considerando que en ese sitio y eliminando el subíndice B, se obtiene:
Esta ecuación muestra claramente que las superficies equipotenciales para una carga puntual aislada son esferas concéntricas a la carga puntual.
Potencial debido a dos cargas puntuales
El potencial en un punto P debido a dos cargas es la suma de los potenciales debido a cada carga individual en dicho punto.
Siendo y las distancias entre las cargas y y el punto P respectivamente.
Potencial eléctrico generado por una distribución discreta de cargas
El potencial en un punto cualquier debido a un grupo de cargas punto se obtiene calculando el potencial debido a cada carga, como si las otras cargas no existieran, y sumando las cantidades así obtenidas, o sea:
siendo el valor de la enésima carga y la distancia de la misma al punto en cuestión. La suma que se efectúa es una suma algebraica y no una suma vectorial. En esto estriba la ventaja de cálculo del potencial sobre la de intensidad del campo eléctrico. Las superficies equipotenciales cortan perpendicularmente a las líneas de campo. En el gráfico se representa la intersección de las superficies equipotenciales con el plano XY.
La ecuación de las líneas equipotenciales es:
Potencial eléctrico generado por una distribución continua de carga
Si la distribución de carga es continua y no una colección de puntos, la suma debe reemplazarse por una integral:
siendo dq un elemento diferencial de la distribución de carga, r su distancia al punto en el cual se calcula V y dV el potencial que dq produce en ese punto.
Potencial eléctrico generado por un plano infinito
Un plano infinito con densidad de carga de superficie crea un campo eléctrico saliente en la dirección perpendicular al plano de valor constante
Si x es la dirección perpendicular al plano y éste se encuentra en x=0 el potencial eléctrico en todo punto x es igual a:
Donde se ha considerado como condición de contorno V(x)=0 en x=0
Distribución de la carga en un conductor en equilibrio
Conductores en equilibrio electrostático

Un material conductor es aquel que permite el transporte de carga eléctrica. En general, los sólidos metálicos son buenos conductores, ya que sus electrones de valencia están poco ligados a los núcleos atómicos, lo que permite que se muevan con facilidad a través del sólido. Este tipo de electrones poco ligados se denominan electrones libres.
Cuando a un sólido conductor cargado con una cierta carga q, se le deja evolucionar la suficiente cantidad de tiempo, alcanza una situación de equilibrio electrostático en la que ya no hay movimiento de cargas. En estas condiciones, el campo en el interior del conductor es nulo (si no, habría movimiento de cargas y no estaría en equilibro).
http://acer.forestales.upm.es/basicas/udfisica/asignaturas/fisica/electro/conductores.html
Pantallas electrostáticas
Física/Electromagnetismo/Pantallas electrostáticas
Poder de las puntas
Física/Electromagnetismo/Poder de las puntas
Generador de Van der Graaff

Un generador de Van der Graaff es un instrumento que lleva carga hacia la superficie de un conductor esférico mediante una cinta transportadora, movida mediante un motor.
Las diferentes aplicaciones de esta máquina incluyen la producción de rayos X, esterilización de alimentos y experimentos de física de partículas y física nuclear.
En la figura adjunta se muestra su funcionamiento: la carga escapa por las puntas de un conductor afilado cerca del fondo del aparato y es captada por la cinta. En la parte superior la carga abandona la cinta y pasa a otro peine metálico conectado a un gran conductor esférico.
Magnetismo
El magnetismo es un fenómeno físico por el que los objetos ejercen fuerzas de atracción o repulsión sobre otros materiales.
Hay materiales que presentan propiedades magnéticas detectables fácilmente, como el níquel, el hierro o el cobalto, que pueden llegar a convertirse en un imán.
Existe un mineral llamado magnetita que es conocido como el único imán natural. De hecho de este mineral proviene el término de magnetismo.
Sin embargo, todos los materiales son influidos, de mayor o menor forma, por la presencia de un campo magnético. El magnetismo es la propiedad algunos objetos que consiste en atraer otros objetos hacia ellos, el imán puede atraer ciertos metales
Fuente: Libro de la SEP ciencias y tecnología (Física secundaria) http://www.endesaeduca.com/Endesa_educa/recursos-interactivos/conceptos-basicos/magnetismo
Imanes naturales
Tienen la propiedad de atraer todas las sustancias magneticas.
Su característica de atraer hierros es natural & no es influida por los seres humanos.
Estan compuestos por el oxido de hierro,son aquellos que se encuentran en la Tierra y que atraen al hierro. Denominados magnetita , hoy sabemos que es hierro cristalino Fe3O4. Pero también la Tierra es un imán natural.
Ondas electromagnéticas
- Historia del Electromagnetismo
- Electrización por inducción
- Electroscopio
- Estructura de la materia
- Fuerzas entre cargas
- Campo eléctrico
- Generalidades Campo eléctrico
- Intensidad de campo
- Potencial
- Líneas de fuerza
- Potencial e intensidad de un punto de un campo radial
- Distribución de la carga en un conductor en equilibrio
- Generador de Van der Graaff
- Electrodinámica
- Ondas electromagnéticas
- Circuito oscilante
- Ondas electromagnéticas
- Gama de ondas electromagnéticas
- Propiedades de las ondas electromagnéticas
Corrientes de alta frecuencia
Física/Electromagnetismo/Corrientes de alta frecuencia
Circuito oscilante
Un procedimiento para producir ondas electromagnéticas de la frecuencia que necesitemos es utilizar un circuito oscilante que está formado por una bobina y un condensador. La frecuencia de oscilación del circuito depende de las características de la bobina y del condensador. En el circuito se produce la transformación de un campo eléctrico entre las placas del condensador, en un campo magnético en el interior de la bobina. El proceso es el siguiente: Circuito oscilante Imagen 7. Elaboración propia. Inicialmente el condensador se encuentra cargado. Toda la energía está en el campo eléctrico. Al cerrar el circuito, el condensador se empieza a descargar, en la bobina se produce una fem autoinducida que se opone al incremento de intensidad. Ésto provoca que la intensidad empiece a disminuir y en la bobina se produce una fem que se opone a que la intensidad disminuya. Esta fem hace que el condensador se cargue con un campo eléctrico opuesto al anterior. El campo magnético desaparece y comienza la descarga siguiendo el proceso contrario al anterior.
Entenderás mejor el proceso observando la animación siguiente, en ella verás como el campo eléctrico del condensador desaparece y aparece un campo magnético en la bobina, y viceversa, de tal modo que se produce una conversión de energía eléctrica en magnética y al revés. Pulsando "energía" puedes ver esta conversión.
Animación 3. Applets de Física Walter Fendt. Uso educativo
En este circuito oscilante la energía se transforma de eléctrica en magnética y viceversa, pero queda almacenada en el circuito sin ser irradiada al exterior. La energía se irradia al exterior separando las armaduras del condensador, como se indica en la animación.
El campo eléctrico deja de estar limitado al espacio entre las armaduras del condensador y tiende a ocupar todo el espacio. Al mismo tiempo, hace lo mismo el campo magnético oscilante creado por la bobina. Las ondas producidas tienen la frecuencia de oscilación del circuito. Esta frecuencia sólo depende de las características de la bobina y del condensador.
En cada punto del espacio que rodea a la antena emisora existe un campo eléctrico variable (azul) que crea a su alrededor un campo magnético variable (rojo), y este campo magnético variable origina un campo eléctrico también variable, y así sucesivamente. Así se propaga la onda electromagnética, generándose mutuamente los campos eléctricos y magnéticos al moverse juntos a la velocidad de la luz.
Radiación. Antenas
Física/Electromagnetismo/Radiación. Antenas
Radiocomunicacion
Física/Electromagnetismo/Radiocomunicacion
Ondas electromagnéticas
Son aquellas ondas que no necesitan un medio material para propagarse. Incluyen, entre otras, la luz visible y las ondas de radio, televisión y telefonía.
Todas se propagan en el vacío a una velocidad constante, muy alta (300 0000 km/s) pero no infinita. Gracias a ello podemos observar la luz emitida por una estrella lejana hace tanto tiempo que quizás esa estrella haya desaparecido ya. O enterarnos de un suceso que ocurre a miles de kilómetros prácticamente en el instante de producirse.
Las ondas electromagnéticas se propagan mediante una oscilación de campos eléctricos y magnéticos. Los campos electromagnéticos al "excitar" los electrones de nuestra retina, nos comunican con el exterior y permiten que nuestro cerebro "construya" el escenario del mundo en que estamos.
Las O.E.M. son también soporte de las telecomunicaciones y el funcionamiento complejo del mundo actual.
Origen y Formación
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas dipolo oscilante
El campo E originado por la carga acelerada depende de la distancia a la carga, la aceleración de la carga y del seno del ángulo que forma la dirección de aceleración de la carga y al dirección al punto en que medimos el campo( sen q).
Un campo electrico variable engendra un campo magnético variable y este a su vez uno electrico, de esta forma las o. e.m. se propagan en el vacio sin soporte material
Características de las ondas electromagnéticas
Los campos producidos por las cargas en movimiento puden abandonar las fuentes y viajar a través del espacio ( en el vacio) creándose y recreándose mutuamente. Lo explica la tercera y cuarta ley de Maxwell.
Las radiaciones electromagnéticas se propagan en el vacio a la velocidad de la luz "c". Y justo el valor de la velocidad de la luz se deduce de las ecuaciones de Maxwell, se halla a partir de dos constantes del medio en que se propaga para las ondas electricas y magnética.
Los campos electricos y magnéticos son perpendiculares entre si ( y perpendiculares a la dirección de propagación) y estan en fase: alcanzan sus valores máximos y mínmos al mismo tiempo y su relación en todo momento está dada por E=c· B
El campo eléctrico procedente de un dipolo está contenido en el plano formado por el eje del dipolo y la dirección de propagación. El enunciado anterior también se cumple si sustituimos el eje del dipolo por la dirección de movimiento de una carga acelerada
Las ondas electromagnéticas son todas semejantes ( independientemente de como se formen) y sólo se diferencian e n su longitud de onda y frecuencia. La luz es una onda electromagnética
Las ondas electromagnéticas transmiten energía incluso en el vacio. Lo que vibra a su paso son los campos eléctricos y magnéticos que crean a propagarse. La vibracion puede ser captada y esa energía absorberse.
Las intensidad instantánea que posee una onda electromagnética, es decir, la energía que por unidad de tiempo atraviesa la unidad de superficie, colocada perpendicularmente a la direción de propagación es: I=c· eoE2. La intensidad media que se propaga es justo la mitad de la expresión anterior. La intensidad de la onda electromagnética al espandirse en el espacio disminuuye con el cuadrado de la distancia y como "I "es proporcional a E2 y por tanto a sen2Q . Por lo tanto existen direcciones preferenciales de propagación
Fuentes
http://teleformacion.edu.aytolacoruna.es/FISICA/document/fisicaInteractiva/Ondasbachillerato/ondasEM/ondasEleMag_indice.htm http://www.areatecnologia.com/ondas-electromagneticas.htm
Gama de ondas electromagnéticas

Todas las ondas electromagnéticas se propagan a la velocidad de la luz, pero difieren unas de otras en el valor de su frecuencia y, por tanto, en el valor de su longitud de onda. Las longitudes de onda varían desde valores muy inferiores al milímetro hasta muy superiores al kilómetro, cubriendo una amplia gama de valores que se denomina espectro electromagnético.
- Las ondas de radio (radioondas) se generan mediante dispositivos electrónicos, sobre todo circuitos oscilantes, y se detectan mediante antenas. Comprenden una amplia región del espectro electromagnético que va desde el orden del centímetro, en las ondas de televisión, hasta el kilómetro en las ondas de radio más largas.
- La radiación de microondas, de longitud de onda entre 0,1mm y 1m, se utiliza en el radar, en astronomía y en los hornos domésticos de microondas.
- La radiación infrarroja, descubierta por Herschel en 1800, es emitida por cuerpos calientes; es muy calorífica y tiene aplicaciones médicas (termografías) e industriales. La fotografía infrarroja se utiliza en la industria textil para diferenciar entre distintos colorantes; también se usa en la detección de falsificaciones de obras de arte, aplicaciones militares, estudios sobre aislantes térmicos, etc.

- La luz visible es la pequeña parte del espectro electromagnético a la que es sensible el ojo humano; su longitud de onda está comprendida entre 400 y 700nm. El estudio de la luz ha constituido una importante rama de la física: la Óptica, que se ocupa del estudio de los fenómenos lumínicos y de los instrumentos ópticos.
- Los rayos ultravioleta (rayos UVA), detectados por Ritter en 1801, son producidos por átomos y moléculas en descargas eléctricas. Impiden la división celular, destruyen microorganismos y producen quemaduras y pigmentación en la piel. El Sol emite grandes cantidades de rayos UVA.
- Los rayos X, descritos por primera vez en 1895 por Rontgen (1845-1923), se producen en las oscilaciones atómicas de la materia. Su longitud de onda está comprendida entre 0,1Å y 30Å. También muy energéticos y penetrantes, son dañinos para los organismos vivos; aunque, como es bien conocido, se utilizan de forma controlada en diagnósticos médicos.
- Los rayos gamma son ondas electromagnéticas de longitud de onda inferior a 0.1Å (1Å=10^-10m); se originan en determinadas desintegraciones nucleares y se encuentran en grandes cantidades en reactores nucleares. Son extremadamente energéticos y penetrantes en la materia.
Propiedades de las ondas electromagnéticas
Las ondas electromagnéticas no necesitan un medio material para propagarse. Así, estas ondas pueden atravesar el espacio interplanetario e interestelar y llegar a la Tierra desde el Sol y las estrellas. Independientemente de su frecuencia y longitud de onda, todas las ondas electromagnéticas se desplazan en el vacío a una velocidad c = 299,792,458 m/s.
Todas las radiaciones del espectro electromagnético presentan las propiedades típicas del movimiento ondulatorio, como la difracción y la interferencia. Las longitudes de onda van desde billonésimas de metro hasta muchos kilómetros. La longitud de onda (λ) y la frecuencia (f) de las ondas electromagnéticas, relacionadas mediante la expresión λ·f = c son importantes para determinar su energía, su visibilidad, su poder de penetración y otras características.
Siendo las siguientes, las propiedades más características de las ondas electromagnéticas.
Reflexión

La reflexión es el cambio de dirección de una onda magnética, que al estar en contacto con la superficie de separación entre dos medios cambiantes, de tal forma que regresa al medio inicial. Ejemplos comunes son la reflexión de la luz, el sonido y las ondas en el agua. La luz es una forma de energía.

Gracias a ello puedes ver tu imagen reflejada en un espejo, en la superficie del agua o un piso muy brillante. Esto se debe a un fenómeno llamado reflexión de la luz.
La reflexión ocurre cuando los rayos que llegan a un medio distinto vuelven a él formando un ángulo igual al de la luz incidente. Es una característica muy distinta a la refracción.
Refracción

La refracción es el cambio de dirección que experimenta una onda al pasar de un medio material a otro. Solo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si estos tienen índices de refracción distintos.

La refracción se origina en el cambio de velocidad de propagación de la onda. Un ejemplo de este fenómeno se ve cuando se sumerge un lápiz en un vaso con agua: el lápiz parece quebrado.
Polarización

La polarización electromagnética es un fenómeno que puede producirse en las ondas electromagnéticas, como la luz, por el cual el campo eléctrico oscila sólo en un plano determinado, denominado plano de polarización. Este plano puede definirse por dos vectores, uno de ellos paralelo a la dirección de propagación de la onda y otro perpendicular a esa misma dirección el cual indica la dirección del campo eléctrico.
En una onda electromagnética no polarizada, al igual que en cualquier otro tipo de onda transversal sin polarizar, el campo eléctrico oscila en todas las direcciones normales a la dirección de propagación de la onda. Las ondas longitudinales, como las ondas sonoras, no pueden ser polarizadas porque su oscilación se produce en la misma dirección que su propagación.
Difracción
La difracción es un fenómeno característico de las ondas que se basa en la desviación de estas al encontrar un obstáculo o al atravesar una rendija. La difracción ocurre en todo tipo de ondas, desde ondas sonoras, ondas en la superficie de un fluido y ondas electromagnéticas como la luz visible y las ondas de radio. También sucede cuando un grupo de ondas de tamaño finito se propaga.
Fenómeno por el cual se produce una desviación de los rayos luminosos cuando pasan por un cuerpo opaco o por una abertura de diámetro menor o igual que la longitud de onda.
Superposición e interferencia
La interferencia es un fenómeno en el que dos o más ondas se superponen para formar una onda resultante de mayor o menor amplitud. El efecto de interferencia puede ser observado en cualquier tipo de ondas, como luz, radio, sonido, ondas en la superficie del agua, etc. Puede producir aleatoriamente aumento, disminución o neutralización del movimiento. Thomas Young fue quien descubrió el fenómeno de la interferencia.
Dispersión
En física se denomina dispersión al fenómeno de separación de las ondas de distinta frecuencia al atravesar un material. Todos los medios materiales son más o menos dispersivos, y la dispersión afecta a todas las ondas; por ejemplo, a las ondas sonoras que se desplazan a través de la atmósfera, a las ondas de radio que atraviesan el espacio interestelar o a la luz que atraviesa el agua, el vidrio o el aire.
Absorción
Las ondas de radio transfieren energía al medio cuando viajan.
Ciertos materiales absorben la radiación y la transforman en calor o energía eléctrica.
La causa de la absorción de las ondas electromagnéticas al viajar por el aire es que el aire no es un vacío, sino que está formado por átomos y moléculas de distintas sustancias gaseosas, líquidas y sólidas. Estos materiales pueden absorber a las ondas electromagnéticas causando pérdidas por absorción. Cuando la onda electromagnética se propaga a través de la atmósfera terrestre, se transfiere energía de la onda a los átomos y moléculas atmosféricos.
La absorción de onda por la atmósfera es análoga a una pérdida de potencia I2R. Una vez absorbida, la energía se pierde para siempre, lo que provoca una atenuación de las intensidades de voltaje y campo magnético al igual que una reducción correspondiente en la densidad de potencia.
Fuentes
Electricidad y magnetismo
Física/Electricidad y magnetismo
Electricidad y electrónica
- Electricidad y electrostática
- Clases de electricidad
- Ley de Ohm
- Condensadores
- Corriente eléctrica
- Intensidad de la corriente
- Resistencia eléctrica
- Transformadores
- Electrización por frotamiento
- Electrización por contacto
Electrostática y electrodinamica
Física/Electricidad y electrónica/Electrostática y electrodinamica
Corriente eléctrica
La corriente o intensidad es la cantidad de electrones que fluyen por la sección transversal de un conductor en un determinado tiempo; su unidad es el Amperio (A).
Intensidad de la corriente
La intensidad de la corriente es la cantidad de electricidad que fluye por la sección transversal de un conductor en un determinado tiempo. La cantidad de electricidad se mide en Culombios en honor a Charles-Augustin de Coulumb y es igual al 6,241506 · 10^18 electrones.
Para medir la intensidad se utiliza un galvanómetro con escala en Amperios, o lo que es lo mismo, un Amperímetro, y se conecta en serie en el circuito.
La intensidad está relaccionada por la Ley de Ohm con la resistencia y la diferencia de potencial.
La fórmula más usada de las que se pueden derivar otras tantas es: V = I / R.
Kirchhoff demostró a través de sus Leyes, que la cantidad de intensidad que entra en un circuito es igual a la que sale.
Ley de Ohm
Conductividad
El científico Georg Simon Ohm, mientras experimentaba con materiales conductores, como resultado de su investigación, llegó a determinar que la relación entre voltaje y corriente era constante y nombró a esta constante resistencia.
Esta ley fue formulada por Georg Simon Ohm en 1827, en la obra Die galvanische Kette, mathematisch bearbeitet (Trabajos matemáticos sobre los circuitos eléctricos), basándose en evidencias empíricas. La formulación original, es:
Siendo la densidad de la corriente, la conductividad eléctrica y el campo eléctrico.
Expresión en función de la resistencia
Como ya se destacó anteriormente, las evidencias empíricas mostraban que (vector densidad de corriente) es directamente proporcional a (vector campo eléctrico). Para escribir ésta relación en forma de ecuación, es necesario añadir una constante denominada factor de conductividad eléctrica, que representaremos como σ. Entonces:
El vector es el vector resultante de los campos que actúan en la sección de alambre que se va a analizar; es decir, del campo producido por la carga del alambre en sí y del campo externo, producido por una batería, una pila u otra fuente de fem. Por lo tanto:
Ahora, sabemos que , donde es un vector unitario de dirección, con lo cual reemplazamos y multiplicamos toda la ecuación por un :
Los vectores y poseen la misma dirección y sentido, con lo cual su producto escalar puede expresarse como el producto de sus magnitudes por el coseno del ángulo formado entre ellos. Es decir:
Por lo tanto, se hace la sustitución:
Integrando ambos miembros en la longitud del conductor:
El miembro derecho representa el trabajo total de los campos que actúan en la sección de alambre que se está analizando, y de cada integral resulta:
y
Donde representa la diferencia de potencial entre los puntos 1 y 2, y representa la fem; por tanto, podemos escribir:
donde representa la caída de potencial entre los puntos 1 y 2.
Como dijimos anteriormente, σ representa la conductividad, por lo que su inversa representará la resistividad, y la representaremos como ρ. Así:
Finalmente, la expresión es lo que se conoce como resistencia eléctrica
Podemos escribir la expresión final:
Ley de Ohm
"La intensidad de la corriente es directamente proporcional al voltaje e inversamente proporcional a la resistencia en todos los circuitos o elementos eléctricos".

La ley de Ohm, es una propiedad específica de ciertos materiales. La relación
es un enunciado de la ley de Ohm. Un conductor cumple con la ley de Ohm sólo si su curva V-I es lineal; esto es si R es independiente de V y de I. La relación
sigue siendo la definición general de la resistencia de un conductor, independientemente de si éste cumple o no con la ley de Ohm. La intensidad de la corriente eléctrica que circula por un dispositivo es directamente proporcional a la diferencia de potencial aplicada e inversamente proporcional a la resistencia del mismo, según expresa la fórmula siguiente:
En donde, empleando unidades del Sistema internacional:
- I = Intensidad en amperios (A).
- V = Diferencia de potencial en voltios (V).
- R = Resistencia en ohmios (Ω).
Resistencia eléctrica
Se denomina resistencia, simbolizada habitualmente como R, a la dificultad u oposición que presenta un cuerpo al paso de una corriente que circula a través del cuerpo. En el Sistema Internacional de Unidades, su valor se expresa en ohms, que se designa con la letra griega omega mayúscula, Ω. Para su medida existen diversos métodos, entre los que se encuentra el uso de un ohmímetro.
La conductividad es la inversa de la resistividad,y su unidad es el S/m (Siemens por metro).
Esta definición es válida para la corriente continua y para la corriente alterna cuando se trate de elementos unicamente resistivos, esto es, sin componente inductiva ni capacitiva. Si existen estos componentes llamados reactivos, la oposición presentada a la circulación de corriente recibe el nombre de impedancia.
-Según sea la magnitud de la resistencia, las sustancias se clasifican en conductoras y aislantes. Otras sustancias llamadas semiconductoras cambian su estado de aislante a conductoras en determinadas condiciones.
-También existen sustancias que presentan un cambio de su valor resistivo dependiendo de las condiciones físicas:
- (NTC ó PTC) varían con el calor.
- (LCR) varían con la luz.
- (VDR)varían con el potencial eléctrico.
Existen además ciertos materiales denominados superconductores, que en determinadas condiciones de temperatura, reducen su valor de resistencia a valores nulos.
Energía y potencial consumida por la corriente
Física/Electricidad y electrónica/Energía y potencial consumida por la corriente
Efectos de la corriente eléctrica
Física/Electricidad y electrónica/Efectos de la corriente eléctrica
Capacidad. Condensadores
- Electricidad y electrostática
- Clases de electricidad
- Ley de Ohm
- Condensadores
- Corriente eléctrica
- Intensidad de la corriente
- Resistencia eléctrica
- Transformadores
- Electrización por frotamiento
- Electrización por contacto
Capacidad de un conductor
Física/Electricidad y electrónica/Capacidad de un conductor
Condensadores
Condensadores con Dieléctricos
Cuando enfrentamos dos conductores sin que haya contacto físico entre ellos, si entre tales conductores enfrentados hay algún tipo de dieléctrico se forma un condensador.
Un dieléctrico es un material que no conduce la electricidad, por lo que puede ser utilizado como aislante; por ejemplo el caucho, la cerámica, la madera seca, el vidrio, el papel, el aire, etc.
Se toma como referencia el valor del condensador cuando no hay nada entre ambos conductores, es decir, cuando hay vacío.
Cuando un material dieléctrico es insertado en un condensador y lo llena por completo, la capacitancia con respecto al vacío aumenta. Para un condensador de placas paralelas aumenta en un factor adimensional k, que es conocido como constante dieléctrica.
Por lo tanto, la capacitancia de un condensador de placas paralelas al que se le ha insertado un dieléctrico entre sus placas, toma el valor (en Faradios):
donde: es 8,8541878176x10-12 F/m.
siendo:
Κ: la constante dieléctrica o permitividad relativa del material dieléctrico entre las placas;
: la permitividad del vacío;
S: el área efectiva de las placas conductoras;
d: la distancia entre las placas o espesor del dieléctrico.
La constante dieléctrica asume distintos valores para los diferentes dieléctricos.
Condensador plano
Física/Electricidad y electrónica/Condensador plano
Asociación de condensadores
Física/Electricidad y electrónica/Asociación de condensadores
Medida de la carga del electrón
Física/Electricidad y electrónica/Medida de la carga del electrón
Energía de un condensador
Física/Electricidad y electrónica/Energía de un condensador
Generadores eléctricos
- Electricidad y electrostática
- Clases de electricidad
- Ley de Ohm
- Condensadores
- Corriente eléctrica
- Intensidad de la corriente
- Resistencia eléctrica
- Transformadores
- Electrización por frotamiento
- Electrización por contacto
Generador eléctrico
Física/Electricidad y electrónica/Generador eléctrico
Fuerza electromotriz
Física/Electricidad y electrónica/Fuerza electromotriz
Ley de Ohm generalizada a un circuito
Física/Electricidad y electrónica/Ley de Ohm generalizada a un circuito
Fuerza electromotriz térmica
Física/Electricidad y electrónica/Fuerza electromotriz térmica
Fuerza electromotriz química: pilas
Física/Electricidad y electrónica/Fuerza electromotriz química: pilas
Fuerza electromotriz inducida
Física/Electricidad y electrónica/Fuerza electromotriz inducida
Campo magnético terrestre
Física/Electricidad y electrónica/Campo magnético terrestre
Propiedades magnéticas de la materia
Física/Electricidad y electrónica/Propiedades magnéticas de la materia
Origen eléctrico del magnetismo
Física/Electricidad y electrónica/Origen eléctrico del magnetismo
Campo magnético originado
Física/Electricidad y electrónica/Campo magnético originado
Acción de un campo magnético
Física/Electricidad y electrónica/Acción de un campo magnético
Corriente alterna
Física/Electricidad y electrónica/Corriente alterna
Fuerza electromotriz inducida
Física/Electricidad y electrónica/Fuerza electromotriz inducida
Autoinducción
Generador de corriente alterna
Física/Electricidad y electrónica/Generador de corriente alterna
Valores eficaces de la corriente alterna
Física/Electricidad y electrónica/Valores eficaces de la corriente alterna
Circuito de corriente alterna
Física/Electricidad y electrónica/Circuito de corriente alterna
Potencia de la corriente alterna
Física/Electricidad y electrónica/Potencia de la corriente alterna
Transformadores
El transformador es un dispositivo que convierte la energía eléctrica alterna de un cierto de nivel de voltaje, en energía alterna de otro nivel de voltaje, por medio de la acción de un campo magnético. Está constituido por dos o más bobinas de alambre, aisladas entre sí eléctricamente por lo general arrolladas alrededor de un mismo núcleo de material ferromagnético. La única conexión entre las bobinas la constituye el flujo magnético común que se establece en el núcleo.
Relación de transformación
La relación de transformación (a) nos indica el aumento ó decremento que sufre el valor de la tensión de salida con respecto a la tensión de entrada, esto quiere decir, por cada volt de entrada cuántos volts hay en la salida del transformador.
Donde: (Np) es el número de espiras del devanado primario, (Ns) es el número de espiras del devanado secundario, (Vp) es la tensión en el devanado primario ó tensión de entrada, (Vs) es la tensión en el devanado secundario ó tensión de salida, (Ip) es la corriente en el devanado primario ó corriente de entrada, e (Is) es la corriente en el devanado secundario ó corriente de salida.
Clasificacion de transformadores
Transformadores elevadores
Este tipo de transformadores nos permiten, como su nombre lo dice elevar la tensión de salida con respecto a la tensión de entrada. Esto quiere decir que la relación de transformación de estos transformadores es menor a uno.
Transformadores variables
Estos transformadores son en realidad auto-transformadores, los cuales debido a su construcción y características pueden ofrecer diferentes valores de voltaje a su salida, ajustando su perilla principal; no asi para su valor de corriente la cual es fija y determinada por el calibre del alambre magneto ( generalmente de cobre ) con el cual fue construido. El nombre Variack viene de una marca norteamericana de gran auge sin embargo no es correcto denominarlos de esta forma.
Transformadores reductores Disminuyen el voltaje que se recibe a la entrada para acoplarlo a las necesidades de los consumidores individuales.
Óptica
Naturaleza de la luz

La luz es una forma de energía que emiten los cuerpos luminosos y que percibimos mediante el sentido de la vista. La luz es una refracción que se propaga en formas de ondas, aunque también se propaga en línea recta en forma de corpúsculos.
Naturaleza de la luz

La luz emitida por las fuentes luminosas es capaz de viajar a través de materia o en ausencia de ella, aunque no todos los medios permiten que la luz se propague
Desde este punto de vista, las diferentes sustancias materiales se pueden clasificar en opacas, traslúcidas y transparentes. Aunque la luz es incapaz de traspasar las opacas, puede atravesar las otras. Las sustancias transparentes tienen, además, la propiedad de que la luz sigue en su interior trayectorias definidas. Éste es el caso del agua, el vidrio o el aire. En cambio, en las traslúcidas la luz se dispersa, lo que da lugar a que a través de ellas no se puedan ver las imágenes con nitidez. El papel vegetal o el cristal esmerilado constituyen algunos ejemplos de objetos traslúcidos.
En un medio que además de ser transparente sea homogéneo, es decir, que mantenga propiedades idénticas en cualquier punto del mismo, la luz se propaga en línea recta. Esta característica, conocida desde la antigüedad, constituye una ley fundamental de la óptica geométrica.

Dado que la luz se propaga en línea recta, para estudiar los fenómenos ópticos de forma sencilla, se acude a algunas simplificaciones útiles. Así, las fuentes luminosas se consideran puntuales, esto es, como si estuvieran concentradas en un punto, del cual emergen rayos de luz o líneas rectas que representan las direcciones de propagación. Un conjunto de rayos que parten de una misma fuente se denomina haz. Cuando la fuente se encuentra muy alejada del punto de observación, a efectos prácticos, los haces se consideran formados por rayos paralelos. Si por el contrario la fuente está próxima la forma del haz es cónica.
La naturaleza de la luz ha sido objeto de la atención de filósofos y científicos desde tiempos remotos. Ya en la antigua Grecia se conocían y se manejaban fenómenos y características de la luz tales como la reflexión, la refracción y el carácter rectilíneo de su propagación, entre otros. No es de extrañar entonces que la pregunta: ¿qué es la luz?, se planteara como una exigencia de un conocimiento más profundo. Los griegos primero y los árabes después sostuvieron que la luz es una emanación del ojo que se proyecta sobre el objeto, se refleja en él y produce la visión. El ojo sería, pues, el emisor y a la vez el receptor de los rayos luminosos.
El modelo corpuscular de Newton
Isaac Newton (1642-1727) se interesó vivamente en los fenómenos asociados a la luz y los colores. A mediados del siglo XVII, propuso una teoría o modelo acerca de lo que es la luz; su aceptación se extendería durante un largo periodo de tiempo. Afirmaba que el comportamiento de la luz en la reflexión y en la refracción podría explicarse con sencillez suponiendo que aquélla consistía en una corriente de partículas que emergen, no del ojo, sino de la fuente luminosa y se dirigen al objeto a gran velocidad describiendo trayectorias rectilíneas. Empleando sus propias palabras, la luz podría considerarse como «multitudes de inimaginables pequeños y velocísimos corpúsculos de varios tamaños».
Al igual que cualquier modelo científico, el propuesto por Newton debería resistir la prueba de los hechos experimentales entonces conocidos, de modo que éstos pudieran ser interpretados de acuerdo con el modelo. Así, explicó la reflexión luminosa asimilándola a los fenómenos de rebote que se producen cuando partículas elásticas chocan contra una pared rígida. En efecto, las leyes de la reflexión luminosa resultaban ser las mismas que las de este tipo de colisiones.
Con el auxilio de algunas suposiciones un tanto artificiales, consiguió explicar también los fenómenos de la refracción, afirmando que cerca de la superficie de separación de dos medios transparentes distintos, los corpúsculos luminosos sufren unas fuerzas atractivas de corto alcance que provocan un cambio en la dirección de su propagación y en su velocidad. Aunque con mayores dificultades que las habidas para explicar la reflexión, logró deducir las leyes de la refracción utilizando el modelo corpuscular.
El modelo ondulatorio de Huygens
El físico Christian Huygens (1629-1695.) dedicó sus esfuerzos a elaborar una teoría ondulatoria acerca de la naturaleza de la luz que con el tiempo vendría a ser la gran rival de la teoría corpuscular de su contemporáneo Newton.
Era un hecho comúnmente aceptado en el mundo científico de entonces, la existencia del «éter cósmico» o medio sutil y elástico que llenaba el espacio vacío. En aquella época se conocían también un buen número de fenómenos característicos de las ondas.
En todos los casos, para que fuera posible su propagación debía existir un medio material que hiciera de soporte de las mismas. Así, el aire era el soporte de las ondas sonoras y el agua el de las ondas producidas en la superficie de un lago.
Huygens supuso que todo objeto luminoso produce perturbaciones en el éter, al igual que un silbato en el aire o una piedra en el agua, las cuales dan lugar a ondulaciones regulares que se propagan a través en todas las direcciones del espacio en forma de ondas esféricas. Además, según Huygens, cuando un punto del éter es afectado por una onda se convierte, al vibrar, en nueva fuente de ondas.
Estas ideas básicas que definen su modelo ondulatorio para la luz le permitieron explicar tanto la propagación rectilínea como los fenómenos de la reflexión y la refracción, que eran, por otra parte, comunes a los diferentes tipos de ondas entonces conocidas. A pesar de la mayor sencillez y el carácter menos artificioso de sus suposiciones, el modelo de Huygens fue ampliamente rechazado por los científicos de su época.
La enorme influencia y prestigio científico adquirido por Newton se aliaron con la falta de un lenguaje matemático adecuado, en contra de la teoría de Huygens para la luz.
El físico inglés Thomas Young (1772-1829) publicó en 1781 un trabajo titulado «Esbozos de experimentos e investigaciones respecto de la luz y el sonido». Utilizando como analogía las ondas en la superficie del agua, descubrió el fenómeno de interferencias luminosas, según el cual cuando dos ondas procedentes de una misma fuente se superponen en una pantalla, aparecen sobre ella zonas de máxima luz y zonas de oscuridad en forma alternada.
El hecho de que, en diferentes zonas, luz más luz pudiese dar oscuridad, fue explicado por Young en base a la teoría ondulatoria, suponiendo que en ellas la cresta de una onda coincidía con el valle de la otra, por lo que se producía una mutua destrucción.
Aunque las ideas de Young tampoco fueron aceptadas de inmediato, el respaldo matemático efectuado por Agustín Fresnel (1788-1827) catorce años después, consiguió poner fuera de toda duda la validez de las ideas de Young sobre tales fenómenos, ideas que se apoyaban en el modelo ondulatorio propuesto por Huygens.
El modelo corpuscular era incapaz de explicar las interferencias luminosas. Tampoco podía explicar los fenómenos de difracción en los cuales la luz parece ser capaz de bordear los obstáculos o doblar las esquinas como lo demuestra la existencia de una zona intermedia de penumbra entre las zonas extremas de luz y sombra. Las ideas de Huygens prevalecían, al fin, sobre las de Newton tras una pugna que había durado cerca de 2 siglos.
La luz como onda electromagnética
El físico escocés James Clerk Maxwell en 1865 situó en la cúspide las primitivas ideas de Huygens, aclarando en qué consistían las ondas luminosas. Al desarrollar su teoría electromagnética demostró matemáticamente la existencia de campos electromagnéticos que, a modo de ondas, podían propagarse tanto por el espacio vacío como por el interior de algunas sustancias materiales.
Maxwell identificó las ondas luminosas con sus teóricas ondas electromagnéticas, prediciendo que éstas deberían comportarse de forma semejante a como lo hacían aquéllas. La comprobación experimental de tales predicciones vino en 1888 de la mano del físico alemán Heinrich Hertz, al lograr situar en el espacio campos electromagnéticos viajeros, que fueron los predecesores inmediatos de las actuales ondas de radio. De esta manera se abría la era de las telecomunicaciones y se hacía buena la teoría de Maxwell de los campos electromagnéticos.
La diferencia entre las ondas de radio (no visibles) y las luminosas tan sólo radicaba en su longitud de onda, desplazándose ambas a la velocidad de la luz, es decir, a 300 000 km/s. Posteriormente una gran variedad de ondas electromagnéticas de diferentes longitudes de onda fueron descubiertas, producidas y manejadas, con lo que la naturaleza ondulatoria de la luz quedaba perfectamente encuadrada en un marco más general y parecía definitiva. Sin embargo, algunos hechos experimentales nuevos mostrarían, más adelante, la insuficiencia del modelo ondulatorio para describir plenamente el comportamiento de la luz.
Los fotones de Einstein
Max Planck (1858-1947), al estudiar los fenómenos de emisión y absorción de radiación electromagnética por parte de la materia, forzado por los resultados de los experimentos, admitió que los intercambios de energía que se producen entre materia y radiación no se llevaban a cabo de forma continua, sino discreta, es decir, como a saltos o paquetes de energía, lo que Planck denominó cuantos de energía.
Esta era una idea radicalmente nueva que Planck intentó conciliar con las ideas imperantes, admitiendo que, si bien los procesos de emisión de luz por las fuentes o los de absorción por los objetos se ve de forma discontinua, la radiación en sí era una onda continua que se propagaba como tal por el espacio.
Así las cosas, Albert Einstein (1879-1955) detuvo su atención sobre un fenómeno entonces conocido como efecto fotoeléctrico. Dicho efecto consiste en que algunos metales como el cesio, por ejemplo, emiten electrones cuando son iluminados por un haz de luz.
El análisis de Einstein reveló que ese fenómeno no podía ser explicado desde el modelo ondulatorio, y tomando como base la idea de discontinuidad planteada con anterioridad por Plank, fue más allá afirmando que no sólo la emisión y la absorción de la radiación se verifica de forma discontinua, sino que la propia radiación es discontinua.
Estas ideas supusieron, de hecho, la reformulación de un modelo corpuscular. Según el modelo de Einstein la luz estaría formada por una sucesión de cuantos elementales que a modo de paquetes de energía chocarían contra la superficie del metal, arrancando de sus átomos los electrones más externos. Estos nuevos corpúsculos energéticos recibieron el nombre de fotones (fotos en griego significa luz).
La luz ¿onda o corpúsculo?
La interpretación efectuada por Einstein del efecto fotoeléctrico fue indiscutible, pero también lo era la teoría de Maxwell de las ondas electromagnéticas.
Ambas habían sido el producto final de la evolución de dos modelos científicos para la luz, en un intento de ajustarlos con más fidelidad a los resultados de los experimentos. Ambos explican la realidad, a pesar de lo cual parecen incompatibles.
Sin embargo, cuando se analiza la situación resultante prescindiendo de la idea de que un modelo deba prevalecer necesariamente sobre el otro, se advierte que de los múltiples fenómenos en los que la luz se manifiesta, unos, como las interferencias o la difracción, pueden ser descritos únicamente admitiendo el carácter ondulatorio de la luz, en tanto que otros, como el efecto fotoeléctrico, se acoplan sólo a una imagen corpuscular. No obstante, entre ambos se obtiene una idea más completa de la naturaleza de la luz. Se dice por ello que son complementarios.
Las controversias y los antagonismos entre las ideas de Newton y Huygens han dejado paso, al cabo de los siglos, a la síntesis de la física actual. La luz es, por tanto, onda, pero también corpúsculo, manifestándose de uno u otro modo en función de la naturaleza del experimento o del fenómeno mediante el cual se la pretende caracterizar o describir.
El Experimentum Crucis de Newton
Newton había encontrado ya que la luz blanca es una luz compuesta, pero deseaba demostrar de una forma indiscutible que los colores que emergían del prisma no eran modificaciones de la luz blanca, como sugerían sus adversarios científicos. Para conseguirlo ideó un «experimentum crucis» o experimento crucial que consistía, en esencia, en someter a cada uno de los colores obtenidos por la acción de un primer prisma, a un segundo prisma, y comprobar por una parte que no podía descomponerse más y por otra su diferente comportamiento en cuanto al grado de desviación sufrida por efecto del prisma. Newton resume sus resultados en los siguientes términos: «En primer lugar descubrí que los rayos que son más refractados que otros de la misma incidencia exhiben colores púrpuras y violetas, mientras que aquellos que exhiben el rojo son menos refractados, y los azules, verdes y amarillos poseen refracciones intermedias... En segundo y a la inversa, descubrí que rayos de igual incidencia son gradualmente más y más refractados según su disposición a exhibir colores en este orden: rojo, amarillo, verde, azul y violeta con todos sus colores intermedios».
El experimento de Young
Su trabajo titulado «Esbozos de experimentos e investigaciones respecto al fondo y a la luz», Thomas Young describe su propio experimento de interferencias luminosas, conocido también como de las dos rendijas. Al igual que Newton, Young empleó la luz solar iluminando de forma controlada un cuarto oscuro.
Dispuso en su interior dos pantallas. Con la primera cubrió la ventana y en ella efectuó dos orificios que permitían el paso de la luz. Sobre la segunda recogía la luz proyectada. Modificando el tamaño de los orificios observó que si éstos eran grandes se formaban dos manchas luminosas y separadas en la segunda pantalla. Pero si los orificios eran suficientemente pequeños, las dos manchas de luz se extendían y sus mitades próximas se superponían una sobre la otra dando lugar a una serie de bandas brillantes separadas por otras oscuras.
Este fenómeno de interferencias luminosas podía ser explicado a partir de la teoría ondulatoria de la luz propuesta por Huygens. Cuando las ondas S y S' procedentes de los focos O y O' respectivamente, llegaban a la pantalla se superponían dando lugar a esa imagen compuesta observada por Young. Dicha superposición podía ser de dos tipos extremos, o bien los valles de la onda S coincidían con los valles de la onda S' (y análogamente para las crestas) o bien un valle de la onda S coincidía en la segunda pantalla con una cresta de la onda S' (y viceversa).
En el primer caso se produciría un refuerzo de la perturbación, lo que podría explicar la existencia de bandas brillantes en esa zona común; la interferencia luminosa habría sido constructiva. En el segundo se produciría una anulación mutua de las perturbaciones al estar dirigidas en sentidos opuestos; la interferencia habría sido destructivo dando lugar a esas zonas oscuras observadas experimentalmente.
La coincidencia o la oposición de las ondas al llegar a la segunda pantalla dependería de las diferencias de distancias entre el punto de confluencia y los focos O y O' respectivos, lo que explicaría que las bandas brillantes y oscuras se alternasen en la pantalla al desplazarnos desde el punto central equidistante de los dos orificios, hacia los extremos de la pantalla.
Propagación de la luz
La propagacion de luz es la cual, se realiza y tiene un entorno muy luminoso el cual se debe ( en breve se completará el artículo)
Propagación rectilínea
Física/Óptica/Propagación rectilínea
Sombras
Velocidad de la luz
Determinación de la velocidad de la luz
En el año 1672 el astrónomo danés Olaf Roëmer consiguió realizar la primera determinación de la velocidad de la luz, considerando para ello distancias interplanetarias.
Al estudiar el periodo de revolución de un satélite (tiempo que emplea en describir una órbita completa) del planeta Júpiter, observó que variaba con la época del año entre dos valores extremos. Roëmer interpretó este hecho como consecuencia de que la Tierra, debido a su movimiento de traslación en torno al Sol, no se encontraba siempre a la misma distancia del satélite, sino que ésta variaba a lo largo del año. Los intervalos medidos representaban realmente la suma del periodo de revolución más el tiempo empleado por la luz en recorrer la distancia entre el satélite y la Tierra. Por esta razón la luz procedente del satélite tardaría más tiempo en llegar al observador cuando éste se encontrase en la posición más alejada, lo que se traduciría en un intervalo de tiempo algo más largo.
La diferencia entre los correspondientes tiempos extremos sería, entonces, el tiempo empleado por la luz en recorrer el diámetro de la órbita terrestre en tomo al Sol. Dado que en su época éste se estimaba en 300 000 000 km y el resultado de dicha diferencia resultó ser de 1 320 segundos, Roëmer, mediante el siguiente cálculo cinemático sencillo:
obtuvo una primera medida del valor de la velocidad c de la luz en el vacío. El valor más preciso obtenido por este método es de 301 500 km/s.
Velocidad e índice de refracción
La velocidad con que la luz se propaga a través de un medio homogéneo y transparente es una constante característica de dicho medio, y por tanto, cambia de un medio a otro.
Debido a su enorme magnitud, la medida de la velocidad de la luz ha requerido la invención de procedimientos ingeniosos que superaran el inconveniente que suponen las cortas distancias terrestres en relación con tan extraordinaria rapidez.
Métodos astronómicos y métodos terrestres han ido dando resultados cada vez más próximos. En la actualidad se acepta para la velocidad de la luz en el vacío el valor c = 299,792,458 m/s. En cualquier medio material transparente la luz se propaga con una velocidad que es siempre inferior a c. Así, por ejemplo, en el agua lo hace a 225 000 km/s y en el vidrio a 195 000 km/s.
Es importante recordar que la velocidad de la luz, así denominada, se refiere a la velocidad de las ondas electromagnéticas, de las cuales, se reconocen como luz, a las del espectro visible, o sea, a las reconocidas por el sorprendente sentido de la vista.
La Permeabilidad Magnética y la Permitividad Eléctrica, definen el vació, rigen el electromagnetismo en el universo y permiten encontrar la velocidad de las ondas electromagnéticas de la siguiente manera:
μo = 4π x 10 E-7 h/m
εo = 8.8541878176x10 E-12 f/m
c = (1/μo·εo) E-2 = 299,792,458 m/s
Estos parámetros, también se usan para definir el comportamiento electromagnético de un material con sus propios valores, los mismos que se relacionan con los valores patrones del vació, mediante las denominadas Permeabilidad Relativa y Permitividad Relativa, ambas adimensionales:
μm = μr . μo, con μr > 1
εm = εr . εo, con εr > 1
Así, con una visión clásica del fenómeno, resulta aceptable, aunque no científicamente correcto, decir que la velocidad de la luz disminuye dependiendo de la red cristalina que atraviesa:
cm = (1/μm·εm) E-2 < 299,792,458 m/s
Sin embargo, en realidad, la energía electromagnética cuando atraviesa un medio material, viaja en el espacio intersticial (vació entre átomos), pero interactuando una y otra vez con los átomos que forman la red cristalina, motivo por el que tarda más en propagarse de un punto a otro.
Una interpretación Cuántica de lo que sucede a nivel de partículas elementales, permite comprender mejor este hecho cuando se observa lo que un "fotón" o partícula de la luz, causa cuando impacta con las partículas materiales o "fermiones". Para ello, debe elaborarse alguno de los complejos y maravillosos diagramas de Richard Feyman, con los que los intercambios de "energía" y "cantidad de movimiento" cuando una partícula de luz impacta sobre una partícula material o cuando esta última emite un "bosón", pueden reflejarse en relaciones matemáticas explícitas.
Nota.- Un "fotón" es una partícula luz y un ejemplo de un "bosón" o partícula de fuerza. Asimismo, un "fermión", es una partícula material, o sea, un electrón o un quark
Indice de refracción
En Óptica se suele comparar la velocidad de la luz en un medio transparente con la velocidad de la luz en el vacío, mediante el llamado índice de refracción absoluto n del medio: se define como el cociente entre la velocidad c de la luz en el vacío y la velocidad v de la luz en el medio, es decir:
Dado que c es siempre mayor que v, n resulta siempre mayor o igual que la unidad. Conforme se deduce de la propia definición cuanto mayor sea el índice de refracción absoluto de una sustancia tanto más lentamente viajará la luz por su interior.
Si lo que se pretende es comparar las velocidades v1 y v2 de dos medios diferentes se define entonces el índice de refracción relativo del medio 1 respecto del 2 como cociente entre ambas:
o en términos de índices de refracción absolutos,
Un índice de refracción relativo menor que 1 indica que en el segundo medio la luz se mueve más "lentamente" que en el primero, puesto que n2 es mayor que n1.
Índices de refracción para varios materiales

| Material | Índice de refracción |
|---|---|
| Vacío | 1.00 |
| Aire | 1.000294 |
| Hielo | 1.31 |
| Agua | 1.33 |
| Alcohol etílico | 1.36 |
| Éter | 1.36 |
| Metacrilato | 1.49 |
| Benceno | 1.50 |
| Vidrio | 1.50 |
| Sal gema | 1.54 |
| Ácido sulfúrico | 1.63 |
| Diamante | 2.42 |
| Cuarzo | 1,54 |
| Glicerina | 1,47 |
| Ácido oleico | 1,46 |
| Metanol | 1,3286 |
| Parafina | 1,43 |
| Jade | 1,66 |
| Amatista | 1,54 - 1,55 |
| Ámbar | 1,54 |
| Azabache | 1,66 |
| Esmeralda | 1,56 - 1,58 |
| Fluorita | 1,433 |
| Zircón | 1,98 |
Óptica geométrica y óptica física
Óptica geométrica
El modelo más sencillo para el estudio de la Óptica es la Óptica geométrica, que parte de las leyes fenomenológicas de Snell de la reflexión y la refracción.
La Óptica geométrica usa la noción de rayo luminoso; es una aproximación del comportamiento que corresponde a las ondas electromagnéticas (la luz) cuando los objetos involucrados son de tamaño mucho mayor que la longitud de onda usada; ello permite despreciar los efectos derivados de la difracción, comportamiento ligado a la naturaleza ondulatoria de la luz. Una formulación alternativa es la de Fermat. Se utiliza en el estudio de la transmisión de la luz por medios homogéneos (lentes, espejos), la reflexión y la refracción.
Óptica física
Cuando los fenómenos ondulatorios comienzan a cobrar importancia, y no se pueden explicar la difracción e interferencia, se requiere de la óptica física, que considera a la luz como una onda transversal, teniendo en cuenta su frecuencia y longitud de onda.
Espectro electromagnético
La óptica física explica los colores como frecuencias distintas de las ondas luminosas y encuadra la luz visible dentro del marco más general del espectro electromagnético.
- Rayos gamma
Su longitud de onda (lambda) < 0.1Å, donde 1Å (Ångström) es igual a 10-10m. Se originan en las desintegraciones nucleares que emiten radiación gamma. Son radiaciones muy penetrantes y muy energéticas.
- Rayos X
Se producen por oscilaciones de los electrones próximos a los núcleos y tienen longitudes de onda entre 0.1Å y 30Å.
Son muy energéticos y penetrantes, dañinos para los organismos vivos, pero se utilizan de forma controlada para los diagnósticos médicos.
- Rayos UVA
Se producen por saltos electrónicos entre átomos y moléculas excitados (30Å-4000Å).
El Sol es emisor de rayos ultravioleta, que son los responsables del bronceado de la piel. Es absorbida por la capa de ozono, y si se recibe en dosis muy grandes puede ser peligrosa ya que impiden la división celular, destruyen microorganismos y producen quemaduras y pigmentación de la piel.
- Luz visible
Es la pequeña parte del espectro electromagnético a la que es sensible el ojo humano (400nm-750nm).
Se producen por saltos electrónicos entre niveles atómicos y moleculares. Las longitudes de onda que corresponden a los colores básicos son:

| Colores | Longitud de onda |
|---|---|
| Rojo | De 6200 a 7500 Å |
| Naranja | De 5900 a 6200 Å |
| Amarillo | De 6200 a 7500 Å |
| Verde | De 5900 a 6200 Å |
| Azul | De 6200 a 7500 Å |
| Violeta | De 5900 a 6200 Å |
- Radiación infrarroja
Es emitida por cuerpos calientes y es debida a vibraciones de los átomos (10-3-10-7m).
La fotografía infrarroja tiene grandes aplicaciones, en la industria textil se utiliza para identificar colorantes, en la detección de falsificaciones de obras de arte, en telemandos, estudios de aislantes térmicos, etc.
- Radiación de microondas
Son producidas por vibraciones de moléculas (0.1mm-1m)
Se utilizan en radioastronomía y en hornos eléctricos. Esta última aplicación es la más conocida hoy en día y en muchos hogares se usan los "microondas". Estos hornos calientan los alimentos generando ondas microondas que en realidad calientan selectivamente el agua. la mayoría de los alimentos, incluso los "secos" contienen agua. Las microondas hacen que las moléculas de agua se muevan, vibran, este movimiento produce fricción y esta fricción el calentamiento. Así no sólo se calienta la comida, otras cosas, como los recipientes, pueden calentarse al estar en contacto con los alimentos.
- Ondas de radio
Son ondas electromagnéticas producidas por el hombre con un circuito oscilante (1cm-1km).
Se emplean en radiodifusión. Las ondas usadas en la televisión son las de longitud de onda menor y las de radio son las de longitud de onda mayor. Las radiondas más largas se reflejan en la ionosfera y se pueden detectar en antenas situadas a grandes distancias del foco emisor. Las ondas medias se reflejan menos en la ionosfera, debido a su gran longitud de onda pueden superar obstáculos, por lo que pueden recorrer grandes distancias. Para superar montañas necesitan repetidores. Las ondas cortas no se reflejan en la ionosfera, requieren repetidores más próximos. Se transmiten a cualquier distancia mediante los satélites artificiales. Este tipo de ondas son las que emiten la TV, teléfonos móviles y los radares.
Reflexión y refracción
Cuando una onda alcanza la superficie de separación de dos medios de distinta naturaleza se producen, en general, dos nuevas ondas, una que retrocede hacia el medio de partida y otra que atraviesa la superficie límite y se propaga en el segundo medio. El primer fenómeno se denomina reflexión y el segundo recibe el nombre de refracción.
El fenómeno de la refracción supone un cambio en la velocidad de propagación de la onda, cambio asociado al paso de un medio a otro de diferente naturaleza o de diferentes propiedades. Este cambio de velocidad da lugar a un cambio en la dirección del movimiento ondulatorio. Como consecuencia, la onda refractada sé desvía un cierto ángulo respecto de la incidente.
La refracción se presenta con cierta frecuencia debido a que los medios no son perfectamente homogéneos, sino que sus propiedades y, por lo tanto, la velocidad de propagación de las ondas en ellos, cambia de un punto a otro. La propagación del sonido en el aire sufre refracciones, dado que su temperatura no es uniforme.
En un día soleado las capas de aire próximas a la superficie terrestre están más calientes que las altas y la velocidad del sonido, que aumenta con la temperatura, es mayor en las capas bajas que en las altas. Ello da lugar a que el sonido, como consecuencia de la refracción, se desvíe hacia arriba. En esta situación la comunicación entre dos personas suficientemente separadas se vería dificultada. El fenómeno contrario ocurre durante las noches, ya que la Tierra se enfría más rápidamente que el aire.
La reflexión de la luz

Al igual que la reflexión de las ondas sonoras, la reflexión luminosa es un fenómeno en virtud del cual la luz al incidir sobre la superficie de los cuerpos cambia de dirección, invirtiéndose el sentido de su propagación. En cierto modo se podría comparar con el rebote que sufre una bola de billar cuando es lanzada contra una de las bandas de la mesa.
La visión de los objetos se lleva a cabo precisamente gracias al fenómeno de la reflexión. Un objeto cualquiera, a menos que no sea una fuente en sí mismo, permanecerá invisible en tanto no sea iluminado. Los rayos luminosos que provienen de la fuente se reflejan en la superficie del objeto y revelan al observador los detalles de su forma y su tamaño.
De acuerdo con las características de la superficie reflectora, la reflexión luminosa puede ser regular o difusa. La reflexión regular tiene lugar cuando la superficie es perfectamente lisa. Un espejo o una lámina metálica pulimentada reflejan ordenadamente un haz de rayos conservando la forma del haz. La reflexión difusa se da sobre los cuerpos de superficies más o menos rugosas.
En ellas un haz paralelo, al reflejarse, se dispersa orientándose los rayos en direcciones diferentes. Ésta es la razón por la que un espejo es capaz de reflejar la imagen de otro objeto en tanto que una piedra, por ejemplo, sólo refleja su propia imagen.
Sobre la base de las observaciones antiguas se establecieron las leyes que rigen el comportamiento de la luz en la reflexión regular o especular. Se denominan genéricamente leyes de la reflexión.
Si S es una superficie especular (representada por una línea recta rayada del lado en que no existe la reflexión), se denomina rayo incidente al que llega a S, rayo reflejado al que emerge de ella como resultado de la reflexión y punto de incidencia O al punto de corte del rayo incidente con la superficie S. La recta N, perpendicular a S por el punto de incidencia, se denomina normal.

La refracción de la luz
Se denomina refracción luminosa al cambio que experimenta la dirección de propagación de la luz cuando atraviesa oblicuamente la superficie de separación de dos medios transparentes de distinta naturaleza. Las lentes, las máquinas fotográficas, el ojo humano y, en general, la mayor parte de los instrumentos ópticos basan su funcionamiento en este fenómeno óptico.
El fenómeno de la refracción va, en general, acompañado de una reflexión, más o menos débil, producida en la superficie que limita los dos medios transparentes. El haz, al llegar a esa superficie límite, en parte se refleja y en parte se refracta, lo cual implica que los haces reflejado y refractado tendrán menos intensidad luminosa que el rayo incidente. Dicho reparto de intensidad se produce en una proporción que depende de las características de los medios en contacto y del ángulo de incidencia respecto de la superficie límite. A pesar de esta circunstancia, es posible fijar la atención únicamente en el fenómeno de la refracción para analizar sus características.
Refracción

Refracción es la desviación que sufre un rayo luminoso al pasar en forma oblicua en un medio transparente a otro de distinta densidad, como es el caso del aire al agua. Se explica la refracción de la luz por que un rayo luminoso al cruzar de un medio a otro diferente cambia su velocidad. El rayo incidente, la normal, y el rayo refractado están en el mismo plano. La relación entre el seno del ángulo de incidencia y el ángulo de refracción es igual a una cantidad constante que se llama índice de refracción.
Leyes de la reflexión y de la refracción
- Básico
- Rayo incidente, es aquel que llega a la superficie de separación de los medios trazados.
- Rayo refractado, el rayo que pasa al otro medio.
- Ángulo de incidencia, el ángulo que se forma entre el incidente y la normal.
- Ángulo de refracción, el ángulo formado por la normal y el rayo refractado.
- Normal, es la perpendicular a la superficie de separación de los medios trazados.
Primera ley
El rayo incidente, la normal y el rayo refractado pertenecen al mismo plano.
Segunda Ley de Snell
La razón o cociente entre el seno del ángulo de incidencia y el seno del ángulo de refracción es una constante, llamada índice de refracción, del segundo medio respecto del primero o sea:
Consideremos dos medios caracterizados por índices de refracción y separados por una superficie S y en los cuales . Los rayos de luz que atraviesen los dos medios se refractarán en la superficie variando su dirección de propagación dependiendo de la diferencia entre los índices de refracción y .
Para un rayo luminoso con un ángulo de incidencia sobre el primer medio, ángulo entre la normal a la superficie y la dirección de propagación del rayo, tendremos que el rayo se propaga en el segundo medio con un ángulo de refracción cuyo valor se obtiene por medio de la ley de Snell.
Observese que para el caso de = 0° (rayos incidentes de forma perpendicular a la superficie) los rayos refractados emergen con un ángulo = 0° para cualquier y . Es decir los rayos que inciden perpendicularmente a un medio no se refractan.
La simetría de la ley de Snell implica que las trayectorias de los rayos de luz es reversible. Es decir, si un rayo incidente sobre la superficie de separación con un ángulo de incidencia se refracta sobre el medio con un ángulo de refracción , entonces un rayo incidente en la dirección opuesta desde el medio 2 con un ángulo de incidencia se refracta sobre el medio 1 con un ángulo .
Una regla cualitativa para determinar la dirección de la refracción es que el rayo en el medio de mayor índice de refracción se acerca siempre a la dirección de la normal a la superficie. La velocidad de la luz en el medio de mayor índice de refracción es siempre menor.
La ley de Snell se puede derivar a partir del principio de Fermat, que indica que la trayectoria de la luz es aquella en la que los rayos de luz necesitan menos tiempo para ir de un punto a otro. En una analogía clásica propuesta por el físico Richard Feynman, el área de un índice de refracción más bajo es substituida por una playa, el área de un índice de refracción más alto por el mar, y la manera más rápida para un socorrista en la playa de rescatar a una persona que se ahoga en el mar es recorrer su camino hasta ésta a través de una trayectoria que verifique la ley de Snell, es decir, recorriendo mayor espacio por el medio más rápido y menor en el medio más lento girando su trayectoria en la intersección entre ambos.
Reflexión interna total (ángulo límite)

Un rayo de luz propagándose en un medio con índice de refracción incidiendo sobre con un ángulo con una superficie sobre un medio de índice con puede reflejarse totalmente en el interior del medio de mayor índice de refracción. Este fenómeno se conoce como reflexión interna total o ángulo límite y se produce para ángulos de incidencia mayores que un valor crítico cuyo valor es:
Discusión de la ley de la refracción
Refracción atmosférica
La densidad de la atmósfera disminuye a medida que nos alejamos de la Tierra. Por eso los rayos luminosos en su trayectoria atraviesan capas de distinta densidad sin solución de continuidad. En dichas circunstancias el rayo se acerca a la normal.
La trayectoria de los rayos configuran una curva, pues la variación de densidad de la atmósfera es gradualmente progresiva debido a que las capas no se presentan perfectamente delimitadas. El astro solamente se observará sin variaciones de altura cuando esta en el cenit.
Por ello es que podemos ver el disco solar al amanecer y al atardecer cuando sólo su borde superior es tangente al horizonte.
Si no existiera refracción atmosférica el cielo ofrecería aspectos distintos.
Ángulo límite
Ángulo límite es el ángulo de incidencia al que corresponde uno de refracción de 90°, cuando el rayo va de un medio más refringente hacia otro menos refringente.
Sea un foco de luz, de él parten infinidad de rayos, y al salir del medio más refringente al menos refringente, los rayos se separan de la normal y, por consiguiente, el ángulo de refracción es mayor que el de incidencia, si éste se va haciendo cada vez mayor llegará un momento en que el rayo salga por la misma superficie de separación de los dos medios y entonces el ángulo de refracción valdrá 90°. El ángulo de incidencia correspondiente se llama ángulo límite. El ángulo límite del agua es 48°; el de vidrio, 42°; el del diamante, 24°, etc.; que corresponden a los índices 1.3 y 2.4 respectivamente.
Reflexión total

En el ángulo límite, el rayo sale por la misma superficie de separación, otro rayo incidente, que forme con la normal un ángulo mayor que el del límite, ya no saldrá al otro medio, sino que quedará dentro del mismo medio. Los ángulos que forman son iguales, como en la reflexión, este fenómeno se llama reflexión total. “Por reflejarse todos los rayos”.
Condiciones. La reflexión total se verifica:
- a) Cuando el rayo va de un medio más refringente hacia otro menos refringente.
- b) Cuando el ángulo de incidencia sea mayor que el del límite.
Ángulo crítico
Puesto que los rayos se alejan de la normal cuando entran en un medio menos denso, y la desviación de la normal aumenta a medida que aumenta el ángulo de incidencia, hay un determinado ángulo de incidencia, denominado ángulo crítico, para el que el rayo refractado forma un ángulo de 90º con la normal, por lo que avanza justo a lo largo de la superficie de separación entre ambos medios. Si el ángulo de incidencia se hace mayor que el ángulo crítico, los rayos de luz serán totalmente reflejados. La reflexión total no puede producirse cuando la luz pasa de un medio menos denso a otro más denso.
Espejismo
Es un fenómeno óptico que consiste en la formación de imágenes invertidas. Se observa en regiones de clima cálido principalmente y se debe a un efecto de reflexión total.
Las capas de aire en contacto con la Tierra, caldeada por el Sol, se calientan extremadamente, y el aire se dispone por capas en orden creciente de densidades de abajo hacia arriba, de modo que las capas más densas están arriba. Esto sucede en días de calma, durante cierto tiempo. En estas condiciones, los rayos de luz que parten del objeto sufren sucesivas refracciones en capas de aire cada vez menos refringente, y llegará el momento en que el ángulo de incidencia sea mayor que el ángulo límite y origine la reflexión total. El objeto se verá invertido, como si se reflejará en el agua de un lago. Esta ilusión se tiene también a veces en los días cálidos en caminos y campos, así como en carreteras asfaltadas, que dan la impresión de que están cubiertas de agua que refleja el cielo. Son capas calientes de aire que reflejan la luz como si fueran un espejo.
Ángulo límite y reflexión total
Cuando un haz luminoso alcanza la superficie de separación de dos medios transparentes, en parte se refracta y en parte se refleja. Si el sentido de la propagación es del medio más refringente al medio menos refringente, el rayo refractado, de acuerdo con la ley de Snell, se alejará de la normal. Eso implica que si se aumenta progresivamente el ángulo de incidencia, el rayo refractado se desviará cada vez más de la normal, aproximándose a la superficie límite hasta coincidir con ella. El valor del ángulo de incidencia que da lugar a este tipo de refracción recibe el nombre de ángulo límite .
La determinación del ángulo límite puede hacerse a partir de la ley de Snell. Dado que el ángulo de refracción que corresponde al ángulo límite vale 90º, se tendrá:
La expresión anterior pone de manifiesto que sólo cuando sea menor que n1 tiene sentido hablar ángulo límite, de lo contrario ( > ) el cociente / sería mayor que la unidad, con lo que no podría definirse, ya que el seno de un ángulo no puede ser mayor que uno.
Para ángulos de incidencias superiores al ángulo límite no hay refracción, sino sólo reflexión, y el fenómeno se conoce como reflexión interna total. También la reflexión total puede ser explicada a partir de la ley de Snell, Puesto que sen <=1, la segunda ley de la refracción se podrá escribir en la forma:
o lo que es lo mismo:
pero / es precisamente y, por tanto:
o en otros términos, la ley de Snell sólo se satisface, si es mayor que , para ángulos de incidencia el menores o iguales al ángulo límite. Para ángulos de incidencia mayores, la refracción no es posible y se produce la reflexión interna total.
Imágenes: sus tipos
En ocasiones los rayos de luz que, procedentes de un objeto, alcanzan el ojo humano y forman una imagen en él, han sufrido transformaciones intermedias debidas a fenómenos ópticos tales como la reflexión o la refracción. Todos los aparatos ópticos, desde el más sencillo espejo plano al más complicado telescopio, proporcionan imágenes más o menos modificadas de los objetos.
La determinación de las relaciones existentes entre un objeto y su imagen correspondiente, obtenida a través de cualquiera de estos elementos o sistemas ópticos, es uno de los propósitos de la óptica geométrica. Su análisis riguroso se efectúa, en forma matemática, manejando convenientemente el carácter rectilíneo de la propagación luminosa junto con las leyes de la reflexión y de la refracción. Pero también es posible efectuar un estudio gráfico de carácter práctico utilizando diagramas de rayos, los cuales representan la marcha de los rayos luminosos a través del espacio que separa el objeto de la imagen.
Presupuestos en que se basa la óptica geométrica
Física/Óptica/Presupuestos en que se basa la óptica geométrica
Convenios de signos
Física/Óptica/Convenios de signos
Difusión
Refracción en una superficie plana
Física/Óptica/Refracción en una superficie plana
Refracción en una lamina y en un prisma
La luz en las láminas
Cuando la luz atraviesa una lámina de material transparente el rayo principal sufre dos refracciones, pues encuentra en su camino dos superficies de separación diferentes. El estudio de la marcha de los rayos cuando la lámina es de caras planas y paralelas, resulta especialmente sencillo y permite familiarizarse de forma práctica con el fenómeno de la refracción luminosa.
En una lámina de vidrio de estas características las normales N y N' a las superficies límites S y S' son también paralelas, por lo que el ángulo de refracción respecto de la primera superficie coincidirá con el de incidencia respecto de la segunda. Si además la lámina está sumergida en un mismo medio como puede ser el aire, éste estará presente a ambos lados de la lámina, de modo que la relación entre los índices de refracción aire-vidrio para la primera refracción será inversa de la correspondiente a la segunda refracción vidrio-aire.
Eso significa que, de acuerdo con la ley de Snell, el rayo refractado en la segunda superficie S' se desviará respecto del incidente alejándose de la normal N' en la misma medida en que el rayo refractado en la superficie S se desvíe respecto de su incidente, en este caso acercándose a la normal.
Esta equivalencia en la magnitud de desviaciones de signo opuesto hace que el rayo que incide en la lámina y el rayo que emerge de ella sean paralelos, siempre que los medios a uno y otro lado sean idénticos. En tal circunstancia las láminas plano-paralelas no modifican la orientación de los rayos que inciden sobre ellas, tan sólo los desplazan.
El prisma óptico

Un prisma óptico es, en esencia, un cuerpo transparente limitado por dos superficies planas no paralelas. El estudio de la marcha de los rayos en un prisma óptico es semejante al realizado para láminas paralelas, sólo que algo más complicado por el hecho de que al estar ambas caras orientadas según un ángulo, las normales correspondientes no son paralelas y el rayo emergente se desvía respecto del incidente.
El prisma óptico fue utilizado sistemáticamente por Isaac Newton en la construcción de su teoría de los colores, según la cual la luz blanca es la superposición de luz de siete colores diferentes, rojo, anaranjado, amarillo, verde, azul, añil y violeta. Experimentos concienzudos realizados con rayos de luz solar y prismas ópticos permitieron a Newton llegar no sólo a demostrar el carácter compuesto de la luz blanca, sino a explicar el fenómeno de la dispersión cromática óptica.
Desde Newton, se sabe que el prisma presenta un grado de refringencia o índice de refracción distinto para cada componente de la luz blanca, por lo que cada color viaja dentro del prisma a diferente velocidad. Ello da lugar, según la ley de Snell, a desviaciones de diferente magnitud de cada uno de los componentes que inciden en el prisma en forma de luz blanca y emergen de él ya descompuestos formando los llamados colores del arco iris. Estas diferentes clases de luz definen la gama conocida como espectro visible. La descomposición es realizada debido a que cada uno de los colores en los que se descompone la luz blanca tiene una frecuencia distinta, por lo que, cada color se desviara un ángulo distinto. El resultado de la desviación produce dicha descomposición cuando sale del prisma.
Refracción atmosférica
Física/Óptica/Refracción atmosférica
Dispersión cromática
Física/Óptica/Dispersión cromática
Instrumentos ópticos
Aparatos ópticos

Por tales se entienden aquellos instrumentos fundados en las propiedades de espejos, prismas y lentes que utiliza el hombre para lograr la visión de objetos muy pequeños o muy alejados en condiciones favorables
Cámara oscura

La cámara oscura es una caja cerrada con un orificio pequeño en una de sus paredes para la entrada de los rayos luminosos (rectos); éstos forman en la pared situada frente al orificio una imagen real invertida de cualquier objeto situado en el exterior delante del orificio. El tamaño de la imagen crece con la distancia entre el orificio y la pared constituida por un vidrio esmerilado (papel de china), donde se forma la imagen. Disminuyendo el diámetro del orificio, la imagen gana en nitidez lo que pierde en luminosidad.
Cámara fotográfica
Es la que consiste esencialmente en una cámara oscura de dimensiones determinadas o bien puede tener un fuelle para alargar o acortar su longitud, en la parte anterior lleva un orificio provisto de un lente convergente, llamada objetivo. En la parte posterior tiene un vidrio esmerilado frente al cual se coloca la placa sensible, recubierta por una capa de bromuro de plata, esta placa es la que va a recibir la imagen cuando entren los rayos de luz a la cámara obscura. Junto a la lente está una lamina que permite la entrada de mayor a menor cantidad de luz, haciendo más grande o más pequeña la abertura por donde ésta pasa, es el diafragma. Además hay otra lámina que abre y cierra la entrada de luz a la cámara, es el obturador.
Cámara cinematográfica
Para impresionar las películas se usa la cámara cinematográfica que no es más que una cámara fotográfica, con la diferencia de que tiene un rollo de película que va pasando rápidamente ante el objetivo, impresionando de 22 a 25 fotografías por segundo, esta película va enrollándose en el mismo aparato, para ser luego revelada y fijada.
Anteojo de Galileo

Este aparato se usa para observaciones a distancia, en él se dispone un ocular constituido por una lente divergente y un objetivo que es una lente convergente, este aparato no da aumentos muy grandes, pero son prácticos por su pequeño tamaño.
Anteojo astronómico

Este aparato, empleado en la observación de los cuerpos celestes consta de dos lentes convergentes: un objetivo y un ocular. El objetivo brinda una imagen real e invertida y mediante el ocular el observador ve una imagen virtual del mismo sentido, es decir invertida respecto al objeto.
La distancia entre el objetivo y el ocular debe ser igual a la suma de sus respectivas distancias focales.
Telescopios

El anteojo astronómico es un telescopio ya que amplifica las imágenes de los cuerpos celestes. Estos se llaman telescopios de refracción, porque las estrellas se ven directamente a través de las lentes que refractan la luz. El moderno telescopio de reflexión un enorme espejo cóncavo el cual recoge la luz de las estrellas y las refleja, concentrando los rayos en un espejo plano, donde son observadas a través de lentes convergentes.
Prismáticos
Es otro tipo de anteojo terrestre con el cual se logra la imagen no invertida, al aplicar dos prismas de reflexión total, en la figura se observa la marcha de los rayos, gracias a las cuatro reflexiones se produce la doble inversión, y la imagen aparece derecha.
Lupa o lente de aumento
Suele llamarse microscopio simple. Es una sencilla lente convergente de pequeña distancia focal; al observar un objeto mediante la misma, su aumento facilita la acomodación; y por lo tanto el ángulo de visión, o diámetro aparente, es notablemente aumentado. La imagen lograda es virtual, mayor y de igual sentido.
Microscopio óptico
El tipo de microscopio más utilizado es el microscopio óptico, que se sirve de la luz visible para crear una imagen aumentada del objeto.
El microscopio óptico más simple es la lente convexa doble con una distancia focal corta. Estos lentes pueden aumentar un objeto hasta 15 veces. Por lo general, se utilizan microscopios compuestos, que disponen de varios lentes con los que se consiguen aumentos mayores. Algunos microscopios ópticos pueden aumentar un objeto por encima de las 2.000 veces.
El microscopio compuesto consiste en dos sistemas de lentes, el objetivo y el ocular, montados en extremos opuestos de un tubo cerrado. El objetivo está compuesto de varias lentes que crean una imagen real aumentada del objeto examinado.
Las lentes de los microscopios están dispuestas de forma que el objetivo se encuentre en el punto focal del ocular. Cuando se mira a través del ocular se ve una imagen virtual aumentada de la imagen real. El aumento total del microscopio depende de las distancias focales de los dos sistemas de lentes.
El equipamiento adicional de un microscopio consta de un armazón con un soporte que sostiene el material examinado y de un mecanismo que permite acercar y alejar el tubo para enfocar la muestra. Los especímenes o muestras que se examinan con un microscopio son transparentes y se observan con una luz que los atraviesa; se suelen colocar sobre un rectángulo fino de vidrio. El soporte tiene un orificio por el que pasa la luz. Bajo el soporte se encuentra un espejo que refleja la luz para que atraviese el espécimen.
El microscopio puede contar con una fuente de luz eléctrica que dirige la luz a través de la muestra.
La fotomicrografía, que consiste en fotografiar objetos a través de un microscopio, utiliza una cámara montada por encima del ocular del microscopio. La cámara suele carecer de objetivo, ya que el microscopio actúa como tal. El término microfotografía, utilizado a veces en lugar de fotomicrografía, se refiere a una técnica de duplicación y reducción de fotografías y documentos a un tamaño minúsculo para guardarlos en un archivo.
Los microscopios que se utilizan en entornos científicos cuentan con varias mejoras que permiten un estudio integral del espécimen. Dado que la imagen de la muestra está ampliada muchas veces e invertida, es difícil moverla de forma manual. Por ello los soportes de los microscopios científicos de alta potencia están montados en una plataforma que se puede mover con tornillos micrométricos. Algunos microscopios cuentan con soportes giratorios. Todos los microscopios de investigación cuentan con tres o más objetivos montados en un cabezal móvil que permite variar la potencia de aumento.
Microscopios ópticos especiales
Hay diversos microscopios ópticos para funciones especiales. Uno de ellos es el microscopio estereoscópico, que no es sino un par de microscopios de baja potencia colocados de forma que convergen en el espécimen. Estos instrumentos producen una imagen tridimensional. El microscopio de luz ultravioleta utiliza el rango ultravioleta del espectro luminoso en lugar del rango visible, bien para aumentar la resolución con una longitud de onda menor o para mejorar el detalle absorbiendo selectivamente distintas longitudes de onda de la banda ultravioleta. Dado que el vidrio no transmite las longitudes de onda más cortas de la luz ultravioleta, los elementos ópticos de estos microscopios están hechos con cuarzo, fluorita o sistemas de espejos aluminizados. Además, dado que la radiación ultravioleta es invisible, la imagen se muestra con fosforescencia, en fotografía o con un escáner electrónico. El microscopio de luz ultravioleta se utiliza en la investigación científica.
El microscopio petrográfico o de polarización se utiliza para identificar y estimar cuantitativamente los componentes minerales de las rocas ígneas y las rocas metamórficas. Cuenta con un prisma de Nicol u otro tipo de dispositivo para polarizar la luz que pasa a través del espécimen examinado. Otro prisma de Nicol o analizador determina la polarización de la luz que ha pasado a través del espécimen. El microscopio tiene un soporte giratorio que indica el cambio de polarización acusado por el espécimen.
El microscopio en campo oscuro utiliza una luz muy intensa en forma de un cono hueco concentrado sobre el espécimen. El campo de visión del objetivo se encuentra en la zona hueca del cono de luz y sólo recoge la luz que se refleja en el objeto. Por ello, las porciones claras del espécimen aparecen como un fondo oscuro y los objetos minúsculos que se están analizando aparecen como una luz brillante sobre el fondo. Esta forma de iluminación se utiliza para analizar elementos biológicos transparentes y sin manchas, invisibles con iluminación normal.
El microscopio de fase ilumina el espécimen con un cono hueco de luz, como en el microscopio en campo oscuro. Sin embargo, en el microscopio de fase el cono de luz es más estrecho y entra en el campo de visión del objetivo, que contiene un dispositivo en forma de anillo que reduce la intensidad de la luz y provoca un cambio de fase de un cuarto de la longitud de onda. Este tipo de iluminación provoca variaciones minúsculas en el índice de refracción de un espécimen transparente, haciéndolo visible. Este tipo de microscopio es muy útil a la hora de examinar tejidos vivos, por lo que se utiliza con frecuencia en biología y medicina.
Entre los microscopios avanzados se encuentra el microscopio de campo cercano, con el que se pueden ver detalles algo menores a la longitud de onda de la luz. Se hace pasar un haz de luz a través de un orificio diminuto y se proyecta a través del espécimen a una distancia equivalente a la mitad del diámetro del orificio, formando una imagen completa.
Microscopio compuesto
Es el microscopio comúnmente conocido y está constituido de manera fundamental por dos lentes: el ocular y el objetivo.
El objetivo: Posee una pequeña distancia focal y está colocado en las cercanías del objeto a observar.
El ocular: Posee una mayor distancia focal que el anterior y es aquel inmediato al ojo del observador.
Ambas lentes están ubicados en un tubo y de tal modo que sus ejes coinciden. Este tubo puede subir o bajar mediante un tornillo micrométrico para lograr el enfoque necesario del objeto. Entonces la imagen obtenida será real, invertida y mayor.
- Usos del Microscopio
a) En la investigación microscópica de metales.
b) En la bacteriología.
c) En Física, Química y Biología.
d) Además en la industria, donde la fotografía microscópica sea indispensable.
Periscopio
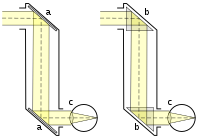
Instrumento óptico para observar desde una posición oculta o protegida. Un periscopio simple consiste en espejos o prismas situados en los extremos opuestos de un tubo con las superficies de reflexión paralelas entre sí en el eje del tubo.
El denominado periscopio de campo o de tanque se ha usado en las trincheras, detrás de parapetos y terraplenes y en tanques, permitiendo ver sin correr riesgos.
El periscopio del submarino es un instrumento más grande y complejo, formado por prismas de reflexión en la parte superior del tubo vertical, con dos telescopios y varias lentes entre ellos y un ocular en la parte inferior. Este periscopio se coloca en un tubo resistente y grueso, de 10 a 15 cm de diámetro, que soporta la presión del agua a grandes profundidades. La única parte giratoria del tubo exterior es la cabeza, fijada al interior del tubo. Ésta puede girarse mediante una palanca o un eje y un engranaje. El campo de visión de un periscopio simple es pequeño, pero algunas mejoras recientes lo han aumentado. El aumento de objetos distantes es de 1,5 a 6 diámetros.
Los periscopios también se usan como dispositivos de avistamiento en aviación militar, en laboratorios físico-nucleares para observar reacciones radiactivas y en aceleradores de partículas.
Estereoscopio

Instrumento óptico a través del cual pueden observarse fotografías de objetos, sino con apariencia sólida y profundidad. Es un instrumento donde se presentan al mismo tiempo dos fotografías del mismo, una a cada ojo. Las dos fotografías están tomadas desde ángulos ligeramente diferentes y se observan a través de dos objetivos con lentes separadas e inclinadas para que coincidan y se fundan las dos imágenes en una tridimensional.
La fotografía espectroscópica aérea permite realizar representaciones en tres dimensiones que pueden utilizarse en la preparación de mapas de relieve.
El ojo
Anatomía del ojo
Física/Óptica/Anatomía del ojo
La visión
Formación de imágenes
Aberración
La óptica geométrica predice que la imagen de un punto formada por elementos ópticos esféricos no es un punto perfecto, sino una pequeña mancha. Las partes exteriores de una superficie esférica tienen una distancia focal distinta a la de la zona central, y este defecto hace que la imagen de un punto sea un pequeño círculo.
|
La diferencia en distancia focal entre las distintas partes de la sección esférica se denomina aberración esférica. |
Si la superficie de una lente o espejo, en lugar de ser una parte de una esfera es una sección de un paraboloide de revolución, los rayos paralelos que inciden en cualquier zona de la superficie se concentran en un único punto, sin aberración esférica. Mediante combinaciones de lentes convexas y cóncavas puede corregirse la aberración esférica, pero este defecto no puede eliminarse con una única lente esférica para un objeto e imagen reales.
Coma

El fenómeno que consiste en un aumento lateral distinto para los puntos del objeto no situados en el eje óptico se denomina coma. Cuando hay coma, la luz procedente de un punto forma una familia de círculos situados dentro de un cono, y en un plano perpendicular al eje óptico la imagen adquiere forma de gota. Escogiendo adecuadamente las superficies puede eliminarse la coma para un determinado par de puntos objeto-imagen, pero no para todos los puntos. Los puntos del objeto y la imagen correspondientes entre sí (o conjugados) para los que no existe aberración esférica ni coma se denominan puntos aplanáticos, y una lente para la que existe dicho par de puntos se denomina lente aplanática.
Astigmatismo
El astigmatismo es un defecto por el que la luz procedente de un punto del objeto situado fuera del eje se esparce en la dirección del eje óptico. Si el objeto es una línea vertical, la sección transversal del haz refractado es una elipse; a medida que se aleja uno de la lente, la elipse se transforma primero en una línea horizontal, luego vuelve a expandirse y posteriormente pasa a ser una línea vertical. Si en un objeto plano, la superficie de mejor enfoque está curvada, se habla de ‘curvatura de imagen’.
La ‘distorsión’ se debe a una variación del aumento con la distancia axial, y no a una falta de nitidez de la imagen.
Aberración cromática lateral

Como el índice de refracción varía con la longitud de onda, la distancia focal de una lente también varía, y produce una ‘aberración cromática’ axial o longitudinal. Cada longitud de onda forma una imagen de tamaño ligeramente diferente; esto produce lo que se conoce por aberración cromática lateral. Mediante combinaciones (denominadas acromáticas) de lentes convergentes y divergentes fabricadas con vidrios de distinta dispersión es posible minimizar la aberración cromática. Los espejos están libres de este defecto. En general, en las lentes acromáticas se corrige la aberración cromática para dos o tres colores determinados.
Defectos del ojo
Física/Óptica/Defectos del ojo
Visión binocular
La visión binocular, con la participación de ambos ojos, permite apreciar las imágenes en tres dimensiones.
Espejos planos

Un espejo plano es una superficie pulida en la que al incidir la luz, se refleja siguiendo las leyes de la reflexión.
Formación de imágenes en espejos planos

Conforme se deduce de las leyes de la reflexión, la imagen P' de un punto objeto P respecto de un espejo plano S' estará situada al otro lado de la superficie reflectora a igual distancia de ella que el punto objeto P. Además la línea que une el punto objeto P con su imagen P' es perpendicular al espejo. Es decir, P y P' son simétricos respecto de S; si se repite este procedimiento de construcción para cualquier objeto punto por punto, se tiene la imagen simétrica del objeto respecto del plano del angulo de incidencia.
Dicha imagen está formada, no por los propios rayos, sino por sus prolongaciones. En casos como éste se dice que la imagen es virtual. Sin embargo, la reflexión en el espejo plano no invierte la posición del objeto. Se trata entonces de una imagen directa.
|
En resumen: la imagen formada en un espejo plano es virtual, directa y de igual tamaño que el objeto. |
Espejos esféricos

Los espejos esféricos tienen la forma de la superficie que resulta cuando una esfera es cortada por un plano. Si la superficie reflectora está situada en la cara interior de la esfera se dice que el espejo es cóncavo. Si está situada en la cara exterior se denomina convexo. Las características ópticas fundamentales de todo espejo esférico son las siguientes:
Su formula es:
n = 360/<a-1
Donde n = numero de imagenes, 360 = < perigonal, < a = angulo de abertura, - 1 = el objeto reflejado.
- Centro de curvatura C: Es el centro de la superficie esférica que constituye el espejo.
- Radio de curvatura R: Es el radio de dicha superficie.
- Vértice V: Coincide con el centro del espejo.
- Eje principal: Es la recta que une el centro de curvatura C con el vértice V.
- Foco: Es un punto del eje por el que pasan o donde convergen todos los rayos reflejados que inciden paralelamente al eje. En los espejos esféricos se encuentra en el punto medio entre el centro de curvatura y el vértice. En linea recta
Formación de imágenes en espejos esféricos
Cuando un rayo incidente pasa por el centro de curvatura, el rayo reflejado recorre el mismo camino, pero en sentido inverso debido a que la incidencia es normal o perpendicular.
Asimismo, cuando un rayo incide paralelamente al eje, el rayo reflejado pasa por el foco, y, viceversa, si el rayo incidente pasa por el foco el reflejado marcha paralelamente al eje. Es ésta una propiedad fundamental de los rayos luminosos que se conoce como reversibilidad.
Con estas reglas, que son consecuencia inmediata de las leyes de la reflexión, es posible construir la imagen de un objeto situado sobre el eje principal cualquiera que sea su posición. Basta trazar dos rayos incidentes que, emergiendo del extremo superior del objeto discurran uno paralelamente al eje y el otro pasando por el centro de curvatura C; el extremo superior del objeto vendrá determinado por el punto en el que ambos rayos convergen. Cuando la imagen se forma de la convergencia de los rayos y no de sus prolongaciones se dice que la imagen es real.
En espejos cóncavos
En la construcción de imágenes en espejos cóncavos y según sea la posición del objeto, se pueden plantear tres situaciones diferentes que pueden ser analizadas mediante diagramas de rayos:
- a) El objeto está situado respecto del eje más allá del centro de curvatura C. En tal caso la imagen formada es real, invertida y de menor tamaño que el objeto.
- b) El objeto está situado entre el centro de curvatura C y el foco F. La imagen resulta entonces real, invertida y de mayor tamaño que el objeto.
- c) El objeto está situado entre el foco F y el vértice V. El resultado es una imagen virtual, directa y de mayor tamaño que el objeto.
En espejos convexos
Para espejos convexos sucede que cualquiera que fuere la distancia del objeto al vértice del espejo la imagen es virtual, directa y de menor tamaño. Dicho resultado puede comprobarse efectuando la construcción de imágenes mediante diagramas de rayos de acuerdo con los criterios anteriormente expuestos.
Su formula es:
n = 360/<a-1.
Donde: n = numero de imagenes, 360 = < perigonal, <a = angulo de abertura, -1 = el objeto reflejado.
- Ampliar en w:Espejo curvo
Lentes
Clasificación de las lentes

a) Lentes convergentes o positivos, son más gruesas por su parte central y más estrechas en los bordes.
b) Lentes divergentes o negativos son más gruesas por los bordes y presentan una estrechez muy pronunciada en el centro
Formación de imágenes a través de las lentes


Las lentes con superficies de radios de curvatura pequeños tienen distancias focales cortas y las lentes con superficie de radios de curvaturas grande tienen distancias focales largas. Una lente con dos superficies convexas siempre refractará los rayos paralelos al eje óptico de forma que converjan en un foco situado en el lado de la lente opuesto al objeto.
Una superficie de lente cóncava desvía los rayos incidentes paralelos al eje de forma divergente; a no ser que la segunda superficie sea convexa y tenga una curvatura mayor que la primera, los rayos divergen al salir de la lente, y parecen provenir de un punto situado en el mismo lado de la lente que el objeto. Estas lentes sólo forman imágenes virtuales, reducidas y no invertidas.
Si la distancia del objeto es mayor que la distancia focal, una lente convergente forma una imagen real e invertida. Si el objeto está lo bastante alejado, la imagen será más pequeña que el objeto. En ese caso, el observador estará utilizando la lente como una lupa o microscopio simple.
El ángulo que forma en el ojo esta imagen virtual aumentada (es decir, su dimensión angular aparente) es mayor que el ángulo que formaría el objeto si se encontrara a la distancia normal de visión.
La relación de estos dos ángulos es la potencia de aumento de la lente. Una lente con una distancia focal más corta crearía una imagen virtual que formaría un ángulo mayor, por lo que su potencia de aumento sería mayor.
La potencia de aumento de un sistema óptico indica cuánto parece acercar el objeto al ojo, y es diferente del aumento lateral de una cámara o telescopio, por ejemplo, donde la relación entre las dimensiones reales de la imagen real y las del objeto aumenta según aumenta la distancia focal.
La cantidad de luz que puede admitir una lente aumenta con su diámetro. Como la superficie que ocupa una imagen es proporcional al cuadrado de la distancia focal de la lente, la intensidad luminosa de la superficie de la imagen es directamente proporcional al diámetro de la lente e inversamente proporcional al cuadrado de la distancia focal.
|
Por ejemplo: la imagen producida por una lente de 3 cm de diámetro y una distancia focal de 20 cm sería cuatro veces menos luminosa que la formada por una lente del mismo diámetro con una distancia focal de 10 cm. La relación entre la distancia focal y el diámetro efectivo de una lente es su relación focal, llamada también número f. Su inversa se conoce como abertura relativa. Dos lentes con la misma abertura relativa tienen la misma luminosidad, independientemente de sus diámetros y distancias focales. |
Fabricación de Lentes:
La mayoría de las lentes están hechas de variedades especiales de vidrio de alta calidad, conocidas como vidrios ópticos, libres de tensiones internas, burbujas y otras imperfecciones.
El proceso de fabricación de una lente a partir de un bloque de vidrio óptico implica varias operaciones. El primer paso consiste en cerrar una lente en bruto a partir del bloque de vidrio. Para ello se presiona el vidrio contra una delgada placa metálica circular que se hace girar. El borde de la placa se carga con polvo de diamante. Después, se le da una primera forma a la pieza en bruto prepulimentándola sobre una placa plana de hierro colado cubierta con una mezcla de granos abrasivos y agua. Para formar la superficie redondeada de la lente se la talla con herramientas cóncavas o convexas cargadas con abrasivos.
La superficie de una lente convexa se forma mediante una herramienta cóncava y viceversa.
Generalmente se emplean dos o más herramientas en este proceso de tallado, utilizando grados de abrasivo cada vez más finos. El último proceso de acabado de la superficie de la lente es el pulido, que se realiza mediante una herramienta de hierro cubierta de brea y bañada con mordiente rojo y agua. Tras el pulido, la lente se 'remata' rectificando el borde hasta que el centro físico coincida con su centro óptico (el centro óptico es un punto tal que cualquier rayo luminoso que pasa por él no sufre desviación). Durante este proceso se coloca la lente en el bastidor de un torno, de forma que su centro óptico se encuentre en el eje de giro, y se rectifican los bordes con una tira de latón cargada con abrasivo.
Caracterización de las Lentes:
Las características ópticas de las lentes sencillas (únicas) o compuestas (sistemas de lentes que contienen dos o más elementos individuales) vienen determinadas por dos factores: la distancia focal de la lente y la relación entre la distancia focal y el diámetro de la lente.
La distancia focal de una lente es la distancia del centro de la lente a la imagen que forma de un objeto situado a distancia infinita.
La distancia focal se mide de dos formas: en unidades de longitud normales, como por ejemplo 20 cm o 1 m, o en unidades llamadas dioptrías, que corresponden al inverso de la distancia focal medida en metros. Por ejemplo, una lente de 1 dioptría tiene una distancia focal de 1 m, y una de 2 dioptrías tiene una distancia focal de 0,5 m. La relación entre la distancia focal y el diámetro de una lente determina su capacidad para recoger luz, o "luminosidad". Esta relación se conoce como número f, y su inversa es la abertura relativa.
Historia:
Las primeras lentes, que ya conocían los griegos y romanos, eran esferas de vidrio llenas de agua. Estas lentes rellenas de agua se empleaban para encender fuego. En la antigüedad clásica no se conocían las auténticas lentes de vidrio; posiblemente se fabricaron por primera vez en Europa a finales del siglo XIII. Los procesos empleados en la fabricación de lentes no han cambiado demasiado desde la Edad Media, salvo el empleo de brea para el pulido, que introdujo Isaac Newton.
El reciente desarrollo de los plásticos y de procesos especiales para moldearlos ha supuesto un uso cada vez mayor de estos materiales en la fabricación de lentes. Las lentes de plástico son más baratas, más ligeras y menos frágiles que las de vidrio.
Tipos de Lentes
Clasificación de las Lentes Convergentes y Divergentes
Las lentes convergentes tienen el espesor de su parte media mayor que el de su parte marginal.
I. Biconvexa o convergente.
II. Plano convexo.
III. Menisco convexa o convergente.
IV. Bicóncava.
V. Plano cóncava.
VI. Menisco cóncava o divergente.
Elementos de una Lente
a) Centro Óptico, donde todo rayo que pasa por él, no sufre desviación.
b) Eje Principal, es la recta que pasa por el centro óptico y por el foco principal.
c) Foco Principal, punto en donde pasan los rayos que son paralelos al eje principal.
d) Eje Secundario, es la recta que pasa por los centros de curvatura.
e) Radios de Curvatura(R1,R2):Son los radios de las esferas que originan la lente.
f) Centros de Curvatura(C1,C2):Son los centros de las esferas que originan la lente.
Rayos notables en las lentes convergentes
1º. Rayo paralelo al eje principal se refracta y pasa por el foco.
2º. El rayo que pasa por el foco principal se refracta y sigue paralelo al eje principal.
3º. Todo rayo que pase por el centro óptico no sufre desviación.
Formación de Imágenes en las Lentes
Para estudiar la formación de imágenes por lentes, es necesario mencionar algunas de las características que permiten describir de forma sencilla la marcha de los rayos.
- Plano óptico. Es el plano central del lente.
- Centro óptico O. Es el centro geométrico del lente. Tiene la propiedad de que todo rayo que pasa por él no sufre desviación alguna.
- Eje principal. Es la recta que pasa por el centro óptico y es perpendicular al plano óptico.
- Focos principales F y F' (foco objeto y foco imagen, respectivamente). Son un par de puntos, correspondientes uno a cada superficie, en donde se cruzan los rayos (o sus prolongaciones) que inciden sobre la lente paralelamente al eje principal.
- Distancia focal f. Es la distancia entre el centro óptico O y el foco F.
- Lentes convergentes. Para proceder a la construcción de imágenes debidas a lentes convergentes, se deben tener presente las siguientes reglas:
Cuando un rayo incide sobre la lente paralelamente al eje, el rayo emergente pasa por el foco imagen F'. Inversamente, cuando un rayo incidente pasa por el foco objeto F, el rayo emergente discurre paralelamente al eje. Finalmente, cualquier rayo que se dirija a la lente pasando por el centro óptico se refracta sin sufrir ninguna desviación.
Lente convergente
Cuando se aplican estas reglas sencillas para determinar la imagen de un objeto por una lente convergente, se obtienen los siguientes resultados:
- Si el objeto está situado respecto del plano óptico a una, la imagen es real, invertida y de menor tamaño.
- Si el objeto está situado a una distancia del plano óptico igual a 2f, la imagen es real, invertida y de igual tamaño.
- Si el objeto está situado a una distancia del plano óptico comprendida entre 2f y f, la imagen es real, invertida y de mayor tamaño.
- Si el objeto está situado a una distancia del plano óptico inferior a f, la imagen es virtual, directa y de mayor tamaño.
Lentes divergentes.
La construcción de imágenes formadas por lentes divergentes se lleva a cabo de forma semejante, teniendo en cuenta que cuando un rayo incide sobre la lente paralelamente al eje, es la prolongación del rayo emergente la que pasa por el foco objeto F. Asimismo, cuando un rayo incidente se dirige hacia el foco imagen F' de modo que su prolongación pase por él, el rayo emergente discurre paralelamente al eje. Finalmente y al igual que sucede en las lentes convergentes, cualquier rayo que se dirija a la lente pasando por el centro óptico se refracta sin sufrir desviación.
Aunque para lentes divergentes se tiene siempre que la imagen resultante es virtual, directa y de menor tamaño, la aplicación de estas reglas permite obtener fácilmente la imagen de un objeto situado a cualquier distancia de la lente.
Construcción gráfica de imágenes en las lentes convergentes
¤ Imágenes reales, son aquellas capaces de ser recibidas sobre una pantalla ubicada en tal forma de que entre ella y el objeto quede la lente.
¤ Imagen virtual, está dada por la prolongación de los rayos refractados, no se puede recibir la imagen en una pantalla.
1º. El objeto está a una distancia doble de la distancia focal. La imagen obtenida es: real, invertida, de igual tamaño, y también a distancia doble de la focal.
2º. El objeto está a distancia mayor que el doble de la distancia focal. Resulta una imagen: real invertida, menor, formada a distancia menor que el objeto.
3º. El objeto está entre el foco y el doble de la distancia focal. La imagen obtenida es: real invertida, mayor, y se forma a mayor distancia que el doble de la focal.
4º. El objeto está entre el foco y el centro óptico. Se obtiene una imagen: virtual, mayor, derecha, formada del lado donde se coloca el objeto.
5º. El objeto está en el foco principal, no se obtiene ninguna imagen.
Lentes convergentes
En los lentes convergentes las imágenes pueden ser reales o virtuales. Fórmula:
Lentes divergentes
En las lentes divergentes las imágenes siempre resultan virtuales, de igual sentido y situados entre la lente y el objeto.
Lentes divergentes. Fórmula:
Potencia de una Lente. Dioptrías.
La potencia de una lente es la inversa de su distancia focal, y la unidad de medida es la dioptría.
Aplicaciones
Las lentes de contacto o las lentes de las gafas o anteojos corrigen defectos visuales. También se utilizan lentes en la cámara fotográfica, el microscopio, el telescopio y otros instrumentos ópticos. Otros sistemas pueden emplearse eficazmente como lentes en otras regiones del espectro electromagnético, como ocurre con las lentes magnéticas usadas en los microscopios electrónicos. (En lo relativo al diseño y uso de las lentes. En lo relativo a la lente del ojo).
Proyector
Cámara fotográfica
Física/Óptica/Cámara fotográfica
Lupa
Microscopio
Anteojos
Telescopio
Óptica física
Principio de Huygens
Física/Óptica/Principio de Huygens
Interferencias luminosas
Se manifiesta cuando dos o más ondas se combinan porque coinciden en el mismo lugar del espacio. Cada onda tiene sus crestas y sus valles, de manera que al coincidir en un momento dado se suman sus efectos. Es frecuente que la interferencia se lleva a cabo entre una onda y su propio reflejo.
Interferencia constructiva: cuando dos ondas interfieren, en los puntos en que coinciden las dos crestas se dice que hay interferencia constructiva. En estos puntos se suman las amplitudes de las ondas.
Interferencia destructiva: al inferir dos ondas, en los puntos donde coincide una cresta de una onda con un valle de la otra onda se dice que hay interferencia destructiva. Las amplitudes en este caso se restan y pueden anularse por completo.
Efecto que se produce cuando dos o más ondas se solapan o entrecruzan. Cuando las ondas interfieren entre sí, la amplitud (intensidad o tamaño) de la onda resultante depende de las frecuencias, fases relativas (posiciones relativas de crestas y valles) y amplitudes de las ondas iniciales; Por ejemplo, la interferencia constructiva se produce en los puntos en que dos ondas de la misma frecuencia que se solapan o entrecruzan están en fase; es decir, cuando las crestas y los valles de ambas ondas coinciden. En ese caso, las dos ondas se refuerzan mutuamente y forman una onda cuya amplitud es igual a la suma de las amplitudes individuales de las ondas originales. La interferencia destructiva se produce cuando dos ondas de la misma frecuencia están completamente desfasadas una respecto a la otra; es decir, cuando la cresta de una onda coincide con el valle de otra. En este caso, las dos ondas se cancelan mutuamente. Cuando las ondas que se cruzan o solapan tienen frecuencias diferentes o no están exactamente en fase ni desfasadas, el esquema de interferencia puede ser más complejo.
La luz visible está formada por ondas electromagnéticas que pueden interferir entre sí. La interferencia de ondas de luz causa, por ejemplo, las irisaciones que se ven a veces en las burbujas de jabón. La luz blanca está compuesta por ondas de luz de distintas longitudes de onda. Las ondas de luz reflejadas en la superficie interior de la burbuja interfieren con las ondas de esa misma longitud reflejadas en la superficie exterior. En algunas de las longitudes de onda, la interferencia es constructiva, y en otras destructiva. Como las distintas longitudes de onda de la luz corresponden a diferentes colores, la luz reflejada por la burbuja de jabón aparece coloreada. El fenómeno de la interferencia entre ondas de luz visible se utiliza en holografía e interferometría.
La interferencia puede producirse con toda clase de ondas, no sólo ondas de luz. Las ondas de radio interfieren entre sí cuando rebotan en los edificios de las ciudades, con lo que la señal se distorsiona. Cuando se construye una sala de conciertos hay que tener en cuenta la interferencia entre ondas de sonido, para que una interferencia destructiva no haga que en algunas zonas de la sala no puedan oírse los sonidos emitidos desde el escenario. Arrojando objetos al agua estancada se puede observar la interferencia de ondas de agua, que es constructiva en algunos puntos y destructiva en otros.
Cuando dos ondas de igual naturaleza se propagan simultáneamente por un mismo medio, cada punto del medio sufrirá la perturbación resultante de componer ambas. Este fenómeno de superposición de ondas recibe el nombre de interferencias y constituye uno de los más representativos del comportamiento ondulatorio.
Lo esencial del fenómeno de interferencias consiste en que la suma de las dos ondas supuestas de igual amplitud no da lugar necesariamente a una perturbación doble, sino que el resultado dependerá de lo retrasada o adelantada que esté una onda respecto de la otra. Se dice que dos ondas alcanzan un punto dado en fase cuando ambas producen en él oscilaciones sincrónicas o acompasadas. En tal caso la oscilación resultante tendrá una amplitud igual a la suma de las amplitudes de las ondas individuales, y la interferencia se denomina constructiva porque en la onda resultante se refuerzan los efectos individuales. Si por el contrario las oscilaciones producidas por cada onda en el punto considerado están contrapuestas, las ondas llegan en oposición de fase y la oscilación ocasionada por una onda será neutralizada por la debida a la otra. En esta situación la interferencia se denomina destructiva.
Si se consideran ondas armónicas unidimensionales y de igual frecuencia, el fenómeno de interferencias puede ser entendido como una consecuencia de las diferencias de distancia de los dos focos y al punto genérico P del un número entero de ondas completas (y de longitudes de onda), eso significa que las ondas individuales llegan en fase a P. Si por el contrario caben un número impar de medias ondas (de semilongitudes de onda ), equivale a decir que las ondas individuales llegan en oposición de fase.
De acuerdo con lo anterior, según sea la posición del punto P del medio respecto de los focos, así será el tipo de interferencias constructiva o destructivo que se darán en él. Cuando se estudia el medio en su conjunto se aprecian puntos en los que ha habido refuerzo y puntos en los que ha habido destrucción mutua de las perturbaciones. Cada uno de tales conjuntos de puntos forma líneas alternativas. El conjunto de líneas de máxima amplitud y de mínima amplitud de oscilación resultante constituye el esquema o patrón de interferencias.
1,643 0
Interferencias en laminas delgadas
Física/Óptica/Interferencias en laminas delgadas
Difraccion

Así como refractar es desviar la difracción es bordear, este fenómeno, está más asociado, con las ondas mecánicas, de una manera más asimilable, pero las ondas electromagnéticas también presentan este fenómeno, prueba de ello es un suceso que ocurrió en un eclipse de sol, mientras se observaba una estrella, el eclipse desviaba los rayos de luz de aquella estrella emisora y daba una ubicación errónea de su situación. Después del eclipse, en la misma noche, se volvió a mirar la estrella y esta se había movido de su anterior ubicación esto indicaba que la luz bordeaba el sol, dando la impresión de dar otra ubicación.
Se basa en la desviación de las ondas al encontrar un obstáculo o al atravesar una rendija. La difracción ocurre en todo tipo de ondas, desde ondas sonoras, ondas en la superficie de un fluido y ondas electromagnéticas como la luz visible y las ondas de radio.
Fenómenos que no se pueden explicar con la teoría corpuscular de la luz
Son: la interferencia, la polarización y la difracción.
Concepto que tenían antiguamente los físicos sobre la sustancia o medio material llamado éter
El éter era una sustancia hipotética que se usaba para justificar los primeros intentos de demostrar la teoría ondulatoria de la luz, el éter, es un medio material, que llenaba el vacío, esta sustancia permitía las perturbaciones típicas de una onda, de tal forma que el medio perturbado era el éter. En ese sentido pudiera atreverme a decir que desde ese punto de vista no había vació en el espacio exterior algo en sí contradictorio.
Cómo esta formadas la luz y cuales son sus características, Según Maxwell
El físico escocés James Clark Maxwell en 1865 situó en la cúspide las primitivas ideas de Huygens, aclarando en qué consistían las ondas luminosas. Al desarrollar su teoría electromagnética demostró matemáticamente la existencia de campos electromagnéticos que, a modo de ondas, podían propagarse tanto por el espacio vacío como por el interior de algunas sustancias materiales.
Maxwell identificó las ondas luminosas con sus teóricas ondas electromagnéticas, prediciendo que éstas deberían comportarse de forma semejante a como lo hacían aquéllas. La comprobación experimental de tales predicciones vino en 1888 de la mano del físico alemán Henrich Hertz, al lograr situar en el espacio campos electromagnéticos viajeros, que fueron los predecesores inmediatos de las actuales ondas de radio. De esta manera se abría la era de las telecomunicaciones y se hacía buena la teoría de Maxwell de los campos electromagnéticos.
La diferencia entre las ondas de radio (no visibles) y las luminosas tan sólo radicaban en su longitud de onda, desplazándose ambas a la velocidad de la luz, es decir, a 300 000 km/s.
Posteriormente una gran variedad de ondas electromagnéticas de diferentes longitudes de onda fue descubierta, producida y manejada, con lo que la naturaleza ondulatoria de la luz quedaba perfectamente encuadrada en un marco más general y parecía definitiva. Sin embargo, algunos hechos experimentales nuevos mostrarían, más adelante, la insuficiencia del modelo ondulatorio para describir plenamente el comportamiento de la luz.
¿Qué descubrimientos hubo al final del siglo XIX, que hicieron renacer la teoría corpuscular de la luz?
Uno de ellos fue el efecto fotoeléctrico. Este efecto consiste en que algunos metales como el cesio, por ejemplo, emiten electrones cuando son iluminados por un haz de luz.
El análisis de Einstein reveló que ese fenómeno no podía ser explicado desde el modelo ondulatorio, y tomando como base la idea de discontinuidad planteada con anterioridad por Plank, fue más allá afirmando que no sólo la emisión y la absorción de la radiación se verifican de forma discontinua, sino que la propia radiación es discontinua.
Estas ideas supusieron, de hecho, la reformulación de un modelo corpuscular. Según el modelo de Einstein la luz estaría formada por una sucesión de cuantos elementales que a modo de paquetes de energía chocarían contra la superficie del metal, arrancando de sus átomos los electrones más externos. Estos nuevos corpúsculos energéticos recibieron el nombre de fotones (fotos en griego significa luz).
Las controversias y los antagonismos entre las ideas de Newton y Huygens han dejado paso, al cabo de los siglos, a la síntesis de la física actual: la luz es, por tanto, onda, pero también corpúsculo, manifestándose de uno u otro modo en función de la naturaleza del experimento o del fenómeno mediante el cual se la pretende caracterizar o describir.
Polarización
Los átomos de una fuente de luz ordinaria emiten pulsos de radiación de duración muy corta. Cada pulso procedente de un único átomo es un tren de ondas prácticamente monocromático (con una única longitud de onda).
El vector eléctrico correspondiente a esa onda no gira en torno a la dirección de propagación de la onda, sino que mantiene el mismo ángulo, o acimut, respecto a dicha dirección. El ángulo inicial puede tener cualquier valor.
Cuando hay un número elevado de átomos emitiendo luz, los ángulos están distribuidos de forma aleatoria, las propiedades del haz de luz son las mismas en todas direcciones, y se dice que la luz no está polarizada. Si los vectores eléctricos de todas las ondas tienen el mismo ángulo acimutal (lo que significa que todas las ondas transversales están en el mismo plano), se dice que la luz está polarizada en un plano, o polarizada linealmente.
Cualquier onda electromagnética puede considerarse como la suma de dos conjuntos de ondas: uno en el que el vector eléctrico vibra formando ángulo recto con el plano de incidencia y otro en el que vibra de forma paralela a dicho plano. Entre las vibraciones de ambas componentes puede existir una diferencia de fase, que puede permanecer constante o variar de forma constante.
Cuando la luz está linealmente polarizada, por ejemplo, esta diferencia de fase se hace 0 o 180°. Si la relación de fase es aleatoria, pero una de las componentes es más intensa que la otra, la luz está en parte polarizada. Cuando la luz es dispersada por partículas de polvo, por ejemplo, la luz que se dispersa en un ángulo de 90°. Con la trayectoria original del haz está polarizada en un plano, lo que explica por qué la luz procedente del cenit está marcadamente polarizada.
Para ángulos de incidencia distintos de 0 o 90°, la proporción de luz reflejada en el límite entre dos medios no es igual para ambas componentes de la luz. La componente que vibra de forma paralela al plano de incidencia resulta menos reflejada. Cuando la luz incide sobre un medio no absorbente con el denominado ángulo de Brewster, llamado así en honor al físico británico del siglo XIX David Brewster, la parte reflejada de la componente que vibra de forma paralela al plano de incidencia se hace nula. Con ese ángulo de incidencia, el rayo reflejado es perpendicular al rayo refractado; la tangente de dicho ángulo de incidencia es igual al cociente entre los índices de refracción del segundo medio y el primero.
Sustancias anisótropas
Algunas sustancias son anisótropas, es decir, muestran propiedades distintas según la dirección del eje a lo largo del cual se midan. En esos materiales, la velocidad de la luz depende de la dirección en que ésta se propaga a través de ellos. Algunos cristales son birrefringentes, es decir, presentan doble refracción. A no ser que la luz se propague de forma paralela a uno de los ejes de simetría del cristal (un eje óptico del cristal), la luz se separa en dos partes que avanzan con velocidades diferentes. Un cristal uniáxico tiene uno de estos ejes. La componente cuyo vector eléctrico vibra en un plano que contiene el eje óptico es el llamado rayo ordinario; su velocidad es la misma en todas las direcciones del cristal, y cumple la ley de refracción de Snell. La componente que vibra formando un ángulo recto con el plano que contiene el eje óptico constituye el rayo extraordinario, y la velocidad de este rayo depende de su dirección en el cristal. Si el rayo ordinario se propaga a mayor velocidad que el rayo extraordinario, la birrefringencia es positiva; en caso contrario la birrefringencia es negativa.
Cuando un cristal es biáxico, la velocidad depende de la dirección de propagación para todas las componentes. Se pueden cortar y tallar los materiales birrefringentes para introducir diferencias de fase específicas entre dos grupos de ondas polarizadas, para separarlos o para analizar el estado de polarización de cualquier luz incidente. Un polarizador sólo transmite una componente de la vibración, ya sea reflejando la otra mediante combinaciones de prismas adecuadamente tallados o absorbiéndola.
El fenómeno por el que un material absorbe preferentemente una componente de la vibración se denomina dicroísmo. El material conocido como Polaroid presenta dicroísmo; está formado por numerosos cristales dicroicos de pequeño tamaño incrustados en plástico, con todos sus ejes orientados de forma paralela. Si la luz incidente es no polarizada, el Polaroid absorbe aproximadamente la mitad de la luz. Los reflejos de grandes superficies planas, como un lago o una carretera mojada, están compuestos por luz parcialmente polarizada, y un Polaroid con la orientación adecuada puede absorberlos en más de la mitad. Este es el principio de las gafas o anteojos de sol Polaroid.
Los llamados analizadores pueden ser físicamente idénticos a los polarizadores. Si se cruzan un polarizador y un analizador situados consecutivamente, de forma que el analizador esté orientado para permitir la transmisión de las vibraciones situadas en un plano perpendicular a las que transmite el polarizador, se bloqueará toda la luz procedente del polarizador.
Las sustancias ‘ópticamente activas’ giran el plano de polarización de la luz linealmente polarizada. Un cristal de azúcar o una solución de azúcar, pueden ser ópticamente activos. Si se coloca una solución de azúcar entre un polarizador y un analizador cruzados tal como se ha descrito antes, parte de la luz puede atravesar el sistema. El ángulo que debe girarse el analizador para que no pase nada de luz permite conocer la concentración de la solución. El polarímetro se basa en este principio.
Algunas sustancias —como el vidrio y el plástico— que no presentan doble refracción en condiciones normales pueden hacerlo al ser sometidas a una tensión. Si estos materiales bajo tensión se sitúan entre un polarizador y un analizador, las zonas coloreadas claras y oscuras que aparecen proporcionan información sobre las tensiones. La tecnología de la fotoelasticidad se basa en la doble refracción producida por tensiones.
También puede introducirse birrefringencia en materiales normalmente homogéneos mediante campos magnéticos y eléctricos. Cuando se somete un líquido a un campo magnético fuerte, puede presentar doble refracción. Este fenómeno se conoce como efecto Kerr, en honor del físico británico del siglo XIX John Kerr. Si se coloca un material apropiado entre un polarizador y un analizador cruzados, puede transmitirse o no la luz según si el campo eléctrico en el material está conectado o desconectado. Este sistema puede actuar como un conmutador o modulador de luz extremadamente rápido.
Fotometría y color
Física/Óptica/Fotometría y color
Manantiales de luz
Física/Óptica/Manantiales de luz
Fotometría
Magnitudes fotometricas
Física/Óptica/Magnitudes fotometricas
Fotómetros
El color de los cuerpos
Física/Óptica/El color de los cuerpos
Mezcla aditiva de colores
Física/Óptica/Mezcla aditiva de colores
Mezcla sustractiva
Física/Óptica/Mezcla sustractiva
Teoría completa del Arco Iris
Teoría completa del Arco Iris
La primera teoría sobre la formación del arco iris se debe a Aristóteles. Para él simplemente era una 'reflexión especial de la luz sobre las nubes, formando un ángulo fijo.
Roger Bacon midió por primera vez el ángulo del arco. Obtuvo 42º para el arco primario y 8º más alto el secundario. (Si tomamos el cambio total de luz sería 138º para el primario y 130º para el secundario).

Teodorico de Freiberg, monje alemán, propone que cada gota es responsable de la formación del arco iris. Esta teoría es corroborada por Descartes tres siglos después.
El arco primario se forma gracias a que la luz se refracta al entrar en la gota y sale tras reflejarse en la cara interna. El arco secundario sufre dos reflexiones. Al haber dos reflexiones en el arco iris secundario, pierde luz respecto al primario, por eso es más débil y más raro de ver en la Naturaleza.
Para una sóla dirección, tanto Teodorico como Descartes se dieron cuenta que dentro del margen de ángulos del arco iris, se veía un sólo color. Había que modificar la posición del observador para observar los otros ángulos de dispersión (y por tanto los colores). Ambos llegaron a la conclusión de que se observan todos los colores en la Naturaleza ya que las gotas de lluvia son muchas y para un observador, se dispersa la luz en toda la gama del espectro.

Los procesos básicos que forman el arco iris son la reflexión y la refracción, o sea, el cambio de dirección en la propagación de la luz debido al cambio del medio material.
El parámetro básico para determinar el cambio de dirección (ángulos de incidencia y salida -ley de Snell-) es el índice de refracción n. Es el cociente entre la velocidad de la luz en el vacío ( aproximadamente) y la velocidad de la misma en el medio.
Se puede realizar un preanálisis sobre el arco iris aplicando sólo las leyes de la reflexión y la refracción. Admitiendo la esfericidad de las gotas, puedo estudiar el sistema en dos dimensiones admitiendo la simetría de revolución para los resultados. La dirección del rayo de luz solar es la horizontal y el único parámetro a tener en cuenta es la distancia al eje diametral de la circunferencia del rayo (llamado parámetro de impacto).

De la imagen de la derecha se desprende que el rayo de clase 1, se da por reflexión directa. El de clase 2 son dos transmisiones (En -1- aire-agua y -2- agua-aire). El de clase tres forma el arco iris primario que se forma tras una refracción en (1), una reflexión en (2) y una refracción en (3). El arco iris secundario se refracta tras dos reflexiones internas (una en (2) y otra en (3)). Puede haber arcos iris superiores (en laboratorio) pero en la Naturaleza no se dan porque la luz ya es muy débil tras las pérdidas por relexión y refracción sucesivas.
Los rayos dependen de su parámetro de impacto b, es decir, la dirección de salida depende de él. Sin embargo los colores se ven bajo un ángulo determinado; en ese ángulo la intensidad de la luz se refuerza... ¿A qué es debido?
Cuando b es cero siguen una trayectoria recta y regresan en la dirección por la que vinieron ( ángulo ). Si aumento b, hasta llegar al radio de la gota el ángulo de desviación disminuye, pasando por un mínimo en , donde R es el radio de la gota, y luego aumenta de nuevo. Este mínimo corresponde al ángulo de 138º de nuestro arco iris primario.
Para el arco iris secundario, el ángulo de desviación es nulo para b=0, y va aumentando mientras aumenta b. Pasa por un máximo donde y disminuye hasta ser de nuevo cero.
Si la gota de agua está uniformemente iluminada, los parámetros de impacto varían de forma continua. Es de esperar que la mayor parte se concentren alrededor del mínimo (3) o el máximo (4), produciéndose la mayor intensidad alrededor de estos ángulos.
Los ángulos de clase (3), del arco iris primario, varían de 180º a 138º y los de clase (4), del arco iris secundario, de 0º a 130º. La intensidad en la franja de 130º a 138º es prácticamente nula. Esto explicaría la zona que existe por encima del arco iris pimario y por debajo del arco iris secundario en la que parece existir una oscuridad relativa. A esta zona se la conoce por banda oscura de Alejandro.
En general hay una redistribución de los rayos y la energía, al ser dispersada la luz por las gotas. Si la dispersión fuese uniforme en el cielo, la luz se distribuiría por igual en cualquier ángulo y todo el cielo estaría uniformemente iluminado.
La teoría de Descartes es sencilla (teoría cartesiana). Hemos de admitir la existencia de rayos de clase superior a (3) y (4), ya que si no la banda oscura de Alejandro sería completamente negra. El brillo viene determinado por la variación de la velocidad del ángulo de desviación, y éste queda determinado por el parámetro de impacto b y el índice de refracción. El radio de la gota es irrelevante, ya que el fenómeno depende de la forma de la misma, no del tamaño.
Demostrar que el ángulo del arco iris primario pasa por un ángulo de aproximadamente 138°.

Sea la circunferencia la proyección en dos dimensiones de una esfera de radio r centrada en O.
La dirección del rayo es representada por la recta . Sin embargo, como b es un parámetro que tomará los valores entre 0 y r, expresaré la recta como , siendo un número entre 0 y 1.
La descripción algebraica de la circunferencia es .
De ambas se deduce que el punto A de incidencia del rayo con la circunferencia es .
La recta que pasa por O y A sería: .
El vector normal interior a la superficie es:
Haciendo el producto vectorial de un vector unitario en la dirección del eje OX, , y el vector normal obtengo:
luego de aquí se deduce que:
Si aplico la ley de Snell: ; siendo n=1 y n' = 4/3.
El ángulo que forma respecto de la horizontal es:
Según observamos en la figura, el triángulo AOB es isósceles de lado r, luego el ángulo de reflexión en B es
El ángulo .
Igualmente en el triángulo OBC, el ángulo del vértice C es . El ángulo de refracción, por la ley de Snell, vuelve a ser . El ángulo total desviado respecto a la horizontal, puedo calcularlo como:
que puede expresarse como: .
es una función de . Puede expresarse como:
Haciendo la derivada:
Igual a cero, para calcular el mínimo, y éste se produce para . Corresponde a un ángulo:

Demostrar que el ángulo del arco iris secundario pasa por un ángulo de aproximadamente 130º.

Nos basamos en la demostración anterior. Se produce una reflexión más. Nuestro objetivo es calcular el ángulo de salida en función de .
El ángulo puede expresarse como (punto C):
De igual forma, el ángulo de salida respecto de la horizontal es:
es una función de . Puede expresarse como:
Haciendo la derivada:
Igual a cero, para calcular el máximo, y éste se produce para . Corresponde a un ángulo:
¿Nos hemos equivocado? Bueno, algo sí. Hemos supuesto que la dirección de impacto es la recta . Si supongo que b<0, entonces es un número entre -1 y 0. Si supongo que el impacto es por encima de la horizontal, en vez de tomar lo tomo como y el ángulo sería .
Sobre los colores
El color debe ser ahora nuestro tema, ya que hasta ahora, no hemos hablado nada de él. Fue Newton el que descubrió que la luz blanca al pasar por un prisma se descompone en un haz de luces monocromáticas. De su experimento se infieren dos aspectos interesantes:
1º) La luz blanca está formada por un conjunto de haces de luz de un sólo color, o monocromáticos.
2º) Materiales como el vidrio presentan un índice de refracción distinto para cada longitud de onda. .
Por tanto, cada rayo de luz monocromático, al pasar por la gota (que se comporta como un prisma) sigue una trayectoria ligeramente diferente del resto de longitudes de onda. Luego cada rayo monocromático presenta un ángulo distinto de arco iris.
Las medidas de Newton fueron, para el arco iris primario de 137º 58' para la luz roja, y 139º 43' para el violeta (una anchura de 1º 45'). Vemos por tanto una superposición de arcos, cada uno de un solo color.
Esto suponiendo que los rayos del Sol vienen paralelos, del infinito. Si acepto una desviación de 0.5º para estos rayos (diámetro aparente del Sol), puedo llegar a un arco de 2º 15' donde recoger todos los arcos de luz monocromáticos.
¿Hemos acabado de explicar el fenómeno del arco iris? Explicamos su angulación, cómo se produce, la oscuridad de su zona superior y los colores... pues no, queda aún más. ¿Os habéis fijado alguna vez en los arcos supernumerarios?.
Arcos supernumerarios. Teoría de Thomas Young.
Aparecen el lado interno del arco primario, en la zona iluminada. En esta zona, hay rayos de clase (3), que tras haber sido difundidos salen con el mismo ángulo, a uno y otro lado del ángulo mínimo del arco iris. Estos rayos han recorrido diferentes caminos en la gota y salen en puntos distintos.

En la época de Descartes o Newton se ignoraba el caracter ondulatorio de la luz, luego no se pudo prever esta interferencia entre estos dos rayos. El primero que dio una explicación coherente fue Young.
Dependiendo de los caminos ópticos que recorre uno más que el otro se presentan franjas brillantes u oscuras (interfieren constructivamente si difieren en valores enteros de longitud de onda).
El camino que recorre el rayo dentro de la gota sí depende del radio (no como antes para los rayos principales), luego su aparición depende del radio de las gotas. Para gotas grandes, los caminos de los rayos difieren más que para gotas pequeñas, y es más difícil que coincidan en longitudes de onda enteras. Para gotas pequeñas los caminos ópticos son prácticamente iguales y es más fácil que interfieran constructivamente. Para radios superiores a 1mm es casi imposible distinguirlos.
La superposición de colores tiende a eliminar también los arcos. Además, como las gotas se hacen más grandes a medida que caen, se explica que se formen inmediatamente debajo del primer arco.
También encontramos una explicación más razonable sobre la banda oscura de Alejandro. La débil luminosidad de la banda no sólo se explica con intensidad residual de arcos iris de clase superior a (4) sino también por fenómenos de difracción.
Así que debemos utilizar, en la explicación de la formación del arco iris, dos teorías de interacción: la de la luz consigo misma (interferencia) y la de la luz con obstáculos (difracción).
Teoría de Airy. Teoría del momento cinético.
En 1835, Richard Potter explicó que el cruce de varios rayos daba lugar a una caústica. Una caústica es la envolvente de un sistema de rayos y se asocia a altos valores de intensidad. La intensidad aumenta hasta llegar a la caústica y luego disminuye rápidamente.

Potter mostró que el rayo de clase 3 de Descartes (desviación mínima) se podría tratar como una caústica. Todo rayo que salga por el lado iluminado se acerca a este rayo en el infinito (no los hay en el lado no iluminado). El problema de hallar la intensidad del arco y su distribución se reduce a determinar la distribución de la misma en la proximidad de la caústica.
Airy fue el primero en intentar demostrar tal distribución. Su razonamiento le hizo usar las teorías de la propagación de la luz de Huygens (mejoradas por Fresnel). Estas decían que cada punto de un frente de ondas se podría reconstruir a partir de estas ondas elementales secundarias como su envolvente.
Según el teorema de Kirchoff, conociendo la distribución de amplitudes de las ondas secundarias de un frente de ondas, puedo saber cuánto vale ésta en otro punto cualesquiera. Podría pues reconstruir los frentes de onda y dar amplitudes en cada punto si conociera un frente de ondas y su valor de amplitudes para una gota. Como ésto es imposible de saber, Airy probó con un frente de ondas inicial escogido según las consideraciones siguientes: 1º) Es normal el frente a todos los rayos de clase (3). 2º) Tiene un punto de inflexiónen el rayo de Descartes (rayo de desviación mínima). 3º) Los valores (amplitudes) se escogieron siguiendo hipótesis normales en la teoría de la difracción.
la distribución de intensidades, tras laborioso cálculo, sale en función de una integral (función de Airy). Esta distribución es análoga a la distribución de intensidades de difracción que aparece en la sombra de un filo rectilíneo para la zona oscura o banda de Alejandro. esta disminuye al alejarnos del ángulo de desviación mínima.
La función de Airy es: , siendo la intensidad de luz transmitida en una situación de interferencia de haces múltiples.
F es la finura: , siendo el coeficiente de reflexión normal aire-agua.
es el desfase que se produce en una lámina plano paralela:
es el ángulo refractado: .
La finura F es aproximadamente 0.085.
Además, predice un máximo importante para el arco primario (con un ángulo algo mayor que el predicho por la teoría de Descartes) y arcos correspondientes a máximos brillantes de la función de difracción que se corresponde con los arcos supernumerarios, reduciéndose en ellos paulatinamente la intensidad. Además, no son tanto en amplitud como en posición los mismos exactamente que predice Young. Tanto Descartes como Young predecían para el ángulo del arco iris una intensidad infinita. Airy sólo le da la mitad del valor de intensidad correspondiente al máximo.
AQUI DEBE IR UNA IMAGEN QUE MUESTRE LA INTENSIDAD EN FUNCION DEL PARAMETRO ALPHA EN LAS TRES TEORIAS.
Los resultados están hechos para un haz de luz monocromático. Para un arco iris real hay que superponer las funciones de intensidad de varios colores. Necesito pues, una teoría sobre el color.
La pureza de los colores viene determinada por el grado de superposición de los arcos iris monocromáticos, que a su vez lo determino a partir del tamaño de las gotas. Las gotas grandes (unos cuantos milímetros) dan colores de arco iris muy puros. Gotas pequeñas (del orden de 0.01 mm) superponen mucho los colores y resulta un arco iris casi blanco.
Otra propiedad de la luz es la polarización. la luz es una onda transversal, es decir, las oscilaciones son perpendiculares a la dirección de propagación. Puede tomarse dos direcciones perpendiculares entre sí y perpendiculares a la dirección de propagación en las que se puede proyectar el campo eléctrico. Si es el vector de ondas (dirección de propagación) y es el vector normal perpendicular al plano de la interfase, se suele tomar una componente (llamada paralela) como la contenida en un plano que definen y , y como otra la perpendicular a y a esta última definida, contenida en el plano de la interfase (llamada transversal).
IMAGEN DE LOS VECTORES K y N
La luz del sol es una mezcla incoherente o al azar de las dos componentes. La reflexión altera el estado de polarización de la luz. Considero la reflexión de la luz en el interior de la gota. ¿Cómo afecta este hecho a la formación del arco iris, bajo el punto de vista de la polarización?
Considérese el plano de la interfase (perpendicular a la normal a la superficie de la imagen - ver imagen -).
IMAGEN DEL ANGULO LIMITE
Considero el ángulo incidente . Si incide enmpezando desde 0º, el poder reflector es pequeño. Pasado el valor dado por la óptica geométrica del ángulo límite, todo se refleja y nada se transmite, independientemente de su polarización.
Métodos de obtención de arco iris hasta de decimotercer orden.
Ampliar en uno el numero de terminos de la ecuacion (añadir una dimension más) y calcular en el espacio decimocuarto
Física moderna
- Introducción
- Cuerpo negro
- Efecto fotoeléctrico
- Efecto Compton
- Dualidad onda-corpúsculo
- Principio de incertidumbre de Heisenberg
- Estructura del átomo
- Protón, electrón y neutrón
- La fisión nuclear
- Masa y energía
- Láseres
- Modelo atómico de Bohr
- Núcleos inestables
Cuerpo negro
Un cuerpo negro es un objeto que absorbe toda la luz y toda la energía que incide sobre él. Ninguna parte de la radiación es reflejada o pasa a través del cuerpo negro. A pesar de su nombre, el cuerpo negro emite la radiación debida a su estado térmico y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862. La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro.
Bases experimentales
Es posible estudiar objetos en el laboratorio con comportamiento muy cercano al del cuerpo negro. Para ello se estudia la radiación proveniente de un agujero pequeño en una cámara aislada. La cámara absorbe muy poca energía del exterior ya que ésta solo puede incidir por el reducido agujero. Sin embargo, la cavidad irradia energía como un cuerpo negro. La luz emitida depende de la temperatura del interior de la cavidad produciendo el espectro de emisión de un cuerpo negro.
Notas históricas
El espectro de emisión de la radiación de cuerpo negro no podía ser explicado con la teoría clásica del electromagnetismo y la mecánica clásica. Estas teorías predecía una intensidad de la radiación a bajas longitudes de onda (altas frecuencias) infinita. A este problema se le conoce como la catástrofe ultravioleta. El problema teórico fue resuelto por Max Planck quién supuso que la radiación electromagnética solo podía propagarse en paquetes de energía discretos a los que llamó quanta. Esta idea fue utilizada poco después por Albert Einstein para explicar el efecto fotoeléctrico. Estos dos trabajos constituyen los cimientos básicos sobre los que se asentó la mecánica cuántica. Hoy llamamos fotones a los quanta de Planck.
Ley de Planck
La intensidad de la radiación emitida por un cuerpo negro con una temperatura T viene dada por la ley de Planck:
donde es la cantidad de energía por unidad de area, unidad de tiempo y unidad de ángulo sólido emitida en el rango de frecuencias entre ν y ν+δν; h es una constante que se conoce como constante de Planck, c es la velocidad de la luz y k es la constante de Boltzmann. La longitud de onda en la que se produce el máximo de emisión viene dada por la ley de Wien y la potencia emitida por unidad de área viene dada por la ley de Stefan-Boltzmann. Por lo tanto, a medida que la temperatura aumenta el brillo de un cuerpo cambia del rojo al amarillo y el azul.
Cuerpos reales y aprox. de cuerpo gris
Los objetos reales nunca se comportan como cuerpos negros ideales. En su lugar, la radiación emitida a una frecuencia dada es una fracción de la emisión ideal. La emisividad de un material específica cuál es la fracción de radiación de cuerpo negro que es capaz de emitir el cuerpo real. La emisividad puede ser distinta en cada longitud de onda y depende de factores tales como la temperatura, condiciones de las superficies (pulidas, oxidadas, limpias, sucias, nuevas o intemperizadas, etc.) y ángulo de emisión. En algunos casos resulta conveniente suponer que existe un valor de emisividad constante para todas las longitudes de onda, siempre menor que 1 (que es la emisividad de un cuerpo negro). Esta aproximación se denomina aproximación de cuerpo gris. La Ley de Kirchhoff indica que la emisividad es igual a la absortividad de manera que un objeto que no es capaz de absorber toda la radiación incidente también emite menos energía que un cuerpo negro ideal.
Efecto fotoeléctrico
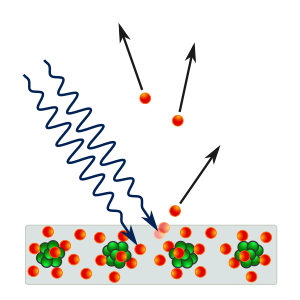
El efecto fotoeléctrico consiste en la emisión de electrones por un material cuando se lo ilumina con radiación electromagnética (luz visible o ultravioleta, en general).
A veces se incluye en el término efecto fotoeléctrico otro dos tipos de interacción entre la luz y la materia:
- Fotoconductividad.
- Es el aumento de la conductividad eléctrica de la materia o en diodos provocada por la luz. Descubierta por Willoughby Smith en el selenio hacia la mitad del siglo 19.
- Efecto fotovoltaico.
- Transformación parcial de la energía luminosa en energía eléctrica. La primera célula solar fue fabricada por Charles Fritts en 1884. Estaba formada por selenio recubierto de una fina capa de oro.
El efecto fotoeléctrico fue descubierto y descrito por Heinrich Hertz en 1887. La explicación teórica solo fue hecha por Albert Einstein en 1905 quien basó su formulación de la fotoelectricidad en una extensión del trabajo sobre los quantos de Max Planck. Más tarde Robert Andrews Millikan pasó diez años a hacer experiencias para demostrar que la teoría de Einstein no era correcta... y demostró que sí lo era. Eso permitió que Einstein y él compartiesen el premio Nobel en 1923.
Formulación del efecto fotoeléctrico
Interpretación cuántica del efecto fotoeléctrico
Los fotones de luz tienen una energía característica determinada por la longitud de onda de la luz. Si un electrón absorbe energía de un fotón y tiene mayor energía que la necesaria para salir del material y que su velocidad está bien dirigida hacia la superficie, entonces el electrón puede ser extraído del material. Si la energía del fotón es demasiado pequeña, el electrón es incapaz de escapar de la superficie del material. Los cambios en la intensidad de la luz no cambian la energía de sus fotones, tan sólo su número y por lo tanto la energía de los electrones emitidos no depende de la intensidad de la luz incidente. Si el fotón es absorbido parte de la energía se utiliza para liberarlo del átomo y el resto contribuye a dotar de energía cinética a la partícula libre.
En principio, todos los electrones son susceptibles de ser emitidos por efecto fotoeléctrico. En realidad los que más salen son los que necesitan lo menos de energía para salir y, de ellos, los más numerosos.
En un aislante (dieléctrico), los electrones más energéticos se encuentran en la banda de valencia. En un metal, los electrones más energéticos están en la banda de conducción. En un semiconductor de tipo N, son los electrones de la banda de conducción que son los más energéticos. En un semiconductor de tipo P también, pero hay muy pocos en la banda de conducción. Así que en ese tipo de semiconductor hay que ir a buscar los electrones de la banda de valencia.
Pero eso no es todo. A la temperatura ambiente, los electrones más energéticos se encuentran cerca del nivel de Fermi (salvo en los semiconductores intrínsecos en los cuales no hay electrones cerca del nivel de Fermi). La energía que hay que dar a un electrón para llevarlo desde el nivel de Fermi hasta el exterior del material se llama función de trabajo. El valor de esa energía es muy variable y depende del material, estado cristalino y, sobre todo de las últimas capas atómicas que recubren la superficie del material. Los metales alcalinos (sodio, calcio, cesio, etc.) presentan las más bajas funciones de trabajo. Aun es necesario que las superficies estén limpias al nivel atómico. Una de la más grandes dificultades de las experiencias de Millikan era había que fabricar las superficies de metal en el vacío.
Formulación matemática
Para analizar el efecto fotoeléctrico cuantitativamente utilizando el método derivado por Einstein es necesario plantear las siguientes ecuaciones:
Energía de un fotón absorbido = Energía necesaria para liberar 1 electrón + energía cinética del electrón emitido.
Algebraicamente:
- ,
que puede también escribirse como
- .
donde h es la constante de Planck, f0 es la frecuencia de corte o frecuencia mínima de los fotones para que tenga lugar el efecto fotoeléctrico, φ es la función de trabajo, o mínima energía necesaria llevar un electrón del nivel de Fermi al exterior del material y Ek es la máxima energía cinética de los electrones que se observa experimentalmente.
- Nota: Si la energía del fotón (hf) no es mayor que la función de trabajo (φ), ningún electrón será emitido.
En algunos materiales esta ecuación describe el comportamiento del efecto fotoeléctrico de manera tan sólo aproximada. Esto es así porque el estado de las superficies no es perfecto (contaminación no uniforme de la superficie).
Dualidad onda-corpúsculo
El efecto fotoeléctrico fue uno de los primeros efectos físicos que puso de manifiesto la dualidad onda-corpúsculo característica de la mecánica cuántica. La luz se comporta como ondas pudiendo producir interferencias y difracción como en el experimento de la doble rendija de Thomas Young, pero intercambia energía de forma discreta en paquetes de energía, fotones, cuya energía depende de la frecuencia de la radiación electromagnética. Las ideas clásicas sobre la absorción de radiación electromagnética por un electrón sugerían que la energía es absorbida de manera continua. Este tipo de explicaciones se encontraban en libros clásicos como el libro de Millikan sobre los Electrones o el escrito por Compton y Allison sobre la teoría y experimentación con rayos X. Estas ideas fueron rápidamente reemplazadas tras la explicación cuántica de Albert Einstein.
Efecto Compton
El efecto Compton consiste en el aumento de la longitud de onda de un fotón de rayos X cuando choca con un electrón libre y pierde parte de su energía. La frecuencia o la longitud de onda de la radiación dispersada depende únicamente de la dirección de dispersión. El desplazamiento de la longitud de onda de los fotones no depende por tanto de la naturaleza del medio en el que se produce la dispersión, sino únicamente de la masa de la partícula que deflecta el fotón (generalmente electrones) y de la dirección de deflexión.
Puede demostrarse a partir del principio de conservación del ímpetu o momento lineal y de la conservación de la energia total que el corrimiento de longitud de onda del fotón viene dado, en función del ángulo de dispersión del fotón respecto a la dirección incidente , supuesta colisión con un electrón:
Que corresponde a una pérdida energética del fotón dada por:
Frecuentemente se define la longitud de onda Compton como .
El efecto compton es un proceso inelástico, por el cual se modifica tanto la dirección como la energia del fotón, en oposición a la dispersión Rayleigh en la que la energia del fotón permanece constante aunque cambia su dirección.
El efecto Compton es predominante a energias del orden de 1 MeV, disminuyendo su sección eficaz con la inversa de la energia para valores altos de esta.
Descubrimiento y relevancia histórica
El efecto Compton fue estudiado por el físico Arthur Compton en 1923 quién pudo explicarlo utilizando la noción cuántica de la radiación electromagnética como cuantos de energía. El efecto Compton constituyó la demostración final de la naturaleza cuántica de la luz tras los estudios de Planck sobre el cuerpo negro y la explicación de Albert Einstein del efecto fotoeléctrico. Como consecuencia de estos estudios Compton ganó el Premio Nobel de Física en 1927.
Efecto Compton inverso
Cuando los fotones chocan con electrones relativistas, pueden ganar inverso. Este efecto puede ser una de las explicaciones de la emisión de rayos X en supernovas, quasars y otros objetos astrofísicos de alta energía.
Dualida onda-corpúsculo

La dualidad onda corpúsculo, también llamada onda partícula, resolvió una aparente paradoja, demostrando que la luz y la materia pueden, a la vez, poseer propiedades de partícula y propiedades ondulatorias.
De acuerdo con la física clásica existen diferencias entre onda y partícula. Una partícula ocupa un lugar en el espacio y tiene masa mientras que una onda se extiende en el espacio caracterizándose por tener una velocidad definida y masa nula.
Actualmente se considera que la dualidad onda - partícula es un “concepto de la mecánica cuántica según el cual no hay diferencias fundamentales entre partículas y ondas: las partículas pueden comportarse como ondas y viceversa.” (Stephen Hawking, 2001)
Fue introducido por Louis-Victor de Broglie, físico francés de principios del siglo XX. En 1924 en su tesis doctoral propuso la existencia de ondas de materia, es decir que toda materia tenía una onda asociada a ella. Esta idea revolucionaria, fundada en la analogía con que la radiación tenía una partícula asociada, propiedad ya demostrada entonces, no despertó gran interés, pese a lo acertado de sus planteamientos, ya que no tenía evidencias de producirse. Sin embargo Einstein reconoció su importancia y cinco años después, en 1929, recibió el Nobel en física por su trabajo.
Su trabajo decía que la longitud de onda, , de la onda asociada a la materia era
donde es la constante de Planck y es la cantidad de movimiento de la partícula de materia.
Principio de incertidumbre de Heisenberg
En mecánica cuántica el principio de indeterminación de Heisenberg afirma que no se puede determinar, simultáneamente y con precisión arbitraria, ciertos pares de variables físicas, como son, por ejemplo, la posición y la cantidad de movimiento de un objeto dado. En palabras sencillas, cuanta mayor certeza se busca en determinar la posición de una partícula, menos se conoce su cantidad de movimiento lineal. Este principio fue enunciado por Werner Heisenberg en 1927.
Definición formal
Si se preparan varias copias idénticas de un sistema en un estado determinado,las medidas de posición y momento (masa x velocidad) de las partículas constituyentes variarán de acuerdo a una cierta distribución de probabilidad característica del estado cuántico del sistema. Las medidas de la desviación estándar Δx de la posición y el momento Δp verifican entonces el principio de incertidumbre que se expresa matemáticamente como:
donde es la constante reducida de Planck, denominada h partida (para simplificar, suele escribirse como [2] )
En la física de sistemas clásicos esta incertidumbre de la posición-momento no se manifiesta puesto que se aplica a estados cuánticos y h es extremadamente pequeño. Una de las formas alternativas del principio de incertidumbre más conocida es la incertidumbre tiempo-energía que puede escribirse como:
Esta forma es la que se utiliza en mecánica cuántica para explorar las consecuencias de la formación de partículas virtuales, utilizadas para estudiar los estados intermedios de una interacción. Esta forma del principio de incertidumbre es también la utilizada para estudiar el concepto de energía del vacío.
Explicación cualitativa
En física clásica, consideramos que tenemos un sistema completamente caracterizado si conocemos las posiciones y el momento de todas sus partículas en un instante dado. Al analizar un sistema que constara de un sólo electrón, Heisenberg encontró que para tratar de determinar la posición con exactitud se necesitarían fotones de alta frecuencia, que al interaccionar con el electrón alterarían significativamente su velocidad. Para tratar de determinar su velocidad con exactitud habría que utilizar fotones de baja energía, que alterasen mínimamente la velocidad de la partícula, pero estos fotones nos darían una visión demasiado "borrosa" de la posición. En suma, encontró que no existía un compromiso posible que nos permitiera medir con precisión ambas variables.
En general, cuando un sistema es lo suficientemente pequeño, no existen métodos físicamente posibles de observarlo sin alterar considerablemente su estado. Volviendo sobre el ejemplo anterior, para que un fotón incida sobre una partícula deberá tener una longitud de onda máxima igual al diámetro de esa partícula (en caso contrario la partícula resulta transparente al fotón) para poder interaccionar. Sabemos que la energía de un fotón es inversamente proporcional a su longitud de onda, en concreto:
E = h c / λ
El Principio cuantifica la máxima precisión que podemos esperar obtener de una observación: el error total en nuestras medidas simultáneas de dos variables conjugadas será siempre como mínimo igual a la constante de Planck dividida por un factor de 4Π. Recordemos que la constante de Planck, de manera muy significativa, corresponde al cuanto de acción, esto es, la acción mínima que se puede ejercer sobre un sistema.
Para comprender este principio es imprescindible que reflexionemos acerca de los procesos que denominamos de "observación" o "medición". Cuando realizamos una medida en un experimento, lo que hacemos es tratar de extraer información de un sistema introduciendo un aparato de medida que, al entrar en contacto con el sistema observado, es alterado por éste. Debemos siempre escoger el aparato de medida de manera que la alteración que produzca en el sistema sea despreciable en comparación a la magnitud de aquello que estamos midiendo. Por ejemplo, si queremos medir la temperatura de un líquido caliente e introducimos en él un termómetro, el líquido cede parte de su calor al mercurio del termómetro. Esta cesión de calor hace que disminuya la temperatura del líquido, pero siempre que haya una cantidad de líquido suficiente, el error que esa disminución produce en la medida será despreciable: la energía intercambiada con el termómetro es insignificante comparada con la energía del sistema que deseamos medir. Cuanto más pequeño y liviano sea el sistema que queremos medir, más sutiles deben ser los aparatos de medida. Cuando lo que tratamos de observar es el mundo subatómico nos encontramos con la imposibilidad física de construir aparatos más sutiles que el sistema que es objeto de estudio.
Consecuencias del principio
Este principio supone un cambio básico en nuestra forma de estudiar la Naturaleza, ya que se pasa de un conocimiento teóricamente exacto (o al menos, que en teoría podría llegar a ser exacto con el tiempo) a un conocimiento basado sólo en probabilidades y en la imposibilidad teórica de superar nunca un cierto nivel de error.
El principio de indeterminación es un resultado teórico entre magnitudes conjugadas (posición - momento, energía-tiempo, etcétera). Un error muy común es decir que el principio de incertidumbre impide conocer con infinita precisión la posición de una partícula o su cantidad de movimiento. Esto es falso. El principio de incertidumbre nos dice que no podemos medir simultáneamente y con infinita precisión un par de magnitudes conjugadas.
Es decir, nada impide que midamos con precisión infinita la posición de una partícula, pero al hacerlo tenemos infinita incertidumbre sobre su momento. Por ejemplo, podemos hacer un montaje como el del experimento de Young y justo a la salida de las rendijas colocamos una pantalla fosforescente de modo que al impactar la partícula se marca su posición con un puntito. Esto se puede hacer, pero hemos perdido toda la información relativa a la velocidad de dicha partícula.
Por otra parte, las partículas en física cuántica no siguen trayectorias bien definidas. No es posible conocer el valor de las magnitudes físicas que describen a la partícula antes de ser medidas. Por lo tanto es falso asignarle una trayectoria a una partícula. Todo lo más que podemos es decir que hay una determinada probabilidad de que la partícula se encuentre en una posición más o menos determinada.
Comúnmente, se considera que el carácter probabilístico de la mecánica cuántica invalida el determinismo científico. Sin embargo, existen varias interpretaciones de la mecánica cuántica y no todas llegan a esta conclusión. Según puntualiza Stephen Hawking, la mecánica cuántica es determinista en sí misma, y es posible que la aparente indeterminación inherente al principio de incertidumbre se deba a que realmente no existen posiciones y velocidades de partículas, sino sólo ondas. Los físicos cuánticos intentarían entonces ajustar las ondas a nuestras ideas preconcebidas de posiciones y velocidades. La inadecuación de estos conceptos sería la causa de la aparente impredecibilidad.
Incertidumbre e indeterminación
Los términos "indeterminación" e "incertidumbre" son equivalentes en este contexto, podemos referirnos al "principio de indeterminación de Heisenberg" o "principio de incertidumbre de Heisenberg" indistintamente.
Artículos relacionados
Referencias
- ↑ Usualmente el punto de referencia se toma como un punto arbitrariamente alejado de las cargas que producen el campo electrostático.
- ↑ . Esta cantidad aparece con mucha frecuencia en la física moderna debido a que, además de su relación con el principio de incertidumbre, es también la unidad básica del momento angular.
Estructura del átomo
El átomo

El átomo es la unidad de partículas más pequeñas que puede existir como sustancia simple (elemento químico), y que puede intervenir en una combinación química Su termino en griego significa “no divisible”, propuesto por Demócrito y Leucipo, quienes suponían que la materia estaba formada por partículas indivisibles e indestructibles. A lo largo de los siglos, el tamaño y la naturaleza del átomo sólo fueron objeto de especulaciones, por lo que su conocimiento avanzó muy lentamente. En los siglos XVI y XVII fue el comienzo y desarrollo de la química experimental, donde el científico inglés John Dalton propuso que la materia está formada por átomos a los cuales asignó una masa característica y que difieren de un elemento, y los representó como esferas macizas e indivisibles.
Mas adelante el físico ingles J.J. Thomson con la ayuda de la utilización de rayos catódicos, propuso un modelo simple de cargas eléctricas negativas (electrones) en el interior de una esfera positiva. Rutherford planteó que en el átomo existe un núcleo con carga positiva y los electrones situados en una corteza girando a su alrededor, como un sistema solar. De igual manera, el físico danés Bohr amplió el modelo de Rutherford, concluyendo que el electrón gira alrededor del núcleo en órbitas circulares y la corteza estaba compuesta de niveles de energía. Posteriormente Sommerfeld propuso que el electrón gira es en órbitas elípticas y no circulares
Todas estas investigaciones del modelo atómico concluyen que la estructura del átomo está formada por una parte central (núcleo), provista de partículas con carga positiva (protones) y a su vez con cargas neutras (neutrones); y por una parte externa (corteza o corona), provista por partículas con carga negativa (electrones). Del núcleo atómico, se derivan las siguientes propiedades: el número atómico (Z), que es el número de protones en el núcleo del átomo, y la posición que ocupa un elemento en la tabla periódica; la masa atómica o numero de masa (A), que es el número total de protones y neutrones presentes en el núcleo.
Todas estas investigaciones del modelo atómico concluyen que la estructura del átomo está formada por una parte central (núcleo), provista de partículas con carga positiva (protones) y a su vez con cargas neutras (neutrones); y por una parte externa (corteza o corona), provista por partículas con carga negativa (electrones). Del núcleo atómico, se derivan las siguientes propiedades: el número atómico (Z), que es el número de protones en el núcleo del átomo, y la posición que ocupa un elemento en la tabla periódica; la masa atómica o numero de masa (A), que es el número total de protones y neutrones presentes en el núcleo.
Hay núcleos de un mismo elemento que contienen el mismo número de protones pero difieren en el número de neutrones o de masa, conocidos como isótopos. Esta diferencia en el número de neutrones no afecta el comportamiento de los átomos, ya que la carga eléctrica o carácter distintivo, depende exclusivamente del número de protones y electrones. Otra propiedad en los átomos es la radiactividad se conoce como la desintegración espontánea de átomos de masa atómica generalmente elevada, con emisión continua de energía bajo la forma de calor, luz, radiaciones y químicas diferentes. Por ejemplo; el uranio de masa atómica 238 se descompone espontáneamente para convertirse en radio de masa atómica 226, y por sucesivas transformaciones termina su período de desintegración al convertirse en plomo.
Estructura atómica
La teoría aceptada hoy es que el átomo se compone de un núcleo de carga positiva formado por protones y neutrones, en conjunto conocidos como nucleones, alrededor del cual se encuentra una nube de electrones de carga negativa.
El núcleo atómico
El núcleo del átomo se encuentra formado por nucleones, los cuales pueden ser de dos clases:
- Protón: Partícula de carga eléctrica positiva igual a una carga elemental, y 1,67262 × 10–27 kg. y una masa 1837 veces mayor que la del electrón
- Neutrón: Partículas carentes de carga eléctrica y una masa un poco mayor que la del protón (1,67493 × 10-27 kg).
El núcleo más sencillo es el del hidrógeno, formado únicamente por un protón. El núcleo del siguiente elemento en la tabla periódica, el helio, se encuentra formado por dos protones y dos neutrones. La cantidad de protones contenidas en el núcleo del átomo se conoce como número atómico, el cual se representa por la letra Z y se escribe en la parte inferior izquierda del símbolo químico. Es el que distingue a un elemento químico de otro. Según lo descrito anteriormente, el número atómico del hidrógeno es 1 (1H), y el del helio, 2 (2He).
La cantidad total de nucleones que contiene un átomo se conoce como número másico, representado por la letra A y escrito en la parte superior izquierda del símbolo químico. Para los ejemplos dados anteriormente, el número másico del hidrógeno es 1(1H), y el del helio, 4(4He).
Existen también átomos que tienen el mismo número atómico, pero diferente número másico, los cuales se conocen como isótopos. Por ejemplo, existen tres isótopos naturales del hidrógeno, el protio (1H), el deuterio (2H) y el tritio (3H). Todos poseen las mismas propiedades químicas del hidrógeno, y pueden ser diferenciados únicamente por ciertas propiedades físicas.
Otros términos menos utilizados relacionados con la estructura nuclear son los isótonos, que son átomos con el mismo número de neutrones. Los isóbaros son átomos que tienen el mismo número másico.
Debido a que los protones tienen cargas positivas se deberían repeler entre sí, sin embargo, el núcleo del átomo mantiene su cohesión debido a la existencia de otra fuerza de mayor magnitud, aunque de menor alcance conocida como la interacción nuclear fuerte.
Interacciones eléctricas entre protones y electrones
Antes del experimento de Rutherford la comunidad científica aceptaba el modelo atómico de Thomson, situación que varió después de la experiencia de Rutherford. Los modelos posteriores se basan en una estructura de los átomos con una masa central cargada positivamente rodeada de una nube de carga negativa.
Este tipo de estructura del átomo llevó a Rutherford a proponer su modelo en que los electrones se moverían alrededor del núcleo en órbitas. Este modelo tiene una dificultad proveniente del hecho de que una partícula cargada acelerada, como sería necesario para mantenerse en órbita, radiaría radiación electromagnética, perdiendo energía. Las leyes de Newton, junto con la ecuaciones de Maxwell del electromagnetismo aplicadas al átomo de Rutherford llevan a que en un tiempo del orden de s, toda la energía del átomo se habría radiado, con el consiguiente caida de los electrones sobre el núcleo.
Corteza
Alrededor del núcleo se encuentran los electrones que son partículas elementales de carga negativa igual a una carga elemental y con una masa de 9,10 × 10–31 kg.
La cantidad de electrones de un átomo en su estado basal es igual a la cantidad de protones que contiene en el núcleo, es decir, al número atómico, por lo que un átomo en estas condiciones tiene una carga eléctrica neta igual a 0.
A diferencia de los nucleones, un átomo puede perder o adquirir algunos de sus electrones sin modificar su identidad química, transformándose en un ion, una partícula con carga neta diferente de cero.
El concepto de que los electrones se encuentran en órbitas satelitales alrededor del núcleo se ha abandonado en favor de la concepción de una nube de electrones deslocalizados o difusos en el espacio, el cual representa mejor el comportamiento de los electrones descrito por la mecánica cuántica únicamente como funciones de densidad de probabilidad de encontrar un electrón en una región finita de espacio alrededor del núcleo.
Dimensiones atómicas
La mayor parte de la masa de un átomo se concentra en el núcleo, formado por los protones y los neutrones, ambos conocidos como nucleones, los cuales son 1836 y 1838 veces más pesados que el electrón respectivamente.
El tamaño o volumen exacto de un átomo es difícil de calcular, ya que las nubes de electrones no cuentan con bordes definidos, pero puede estimarse razonablemente en 1,0586 × 10–10 m, el doble del radio de Bohr para el átomo de hidrógeno. Si esto se compara con el tamaño de un protón, que es la única partícula que compone el núcleo del hidrógeno, que es aproximadamente 1 × 10–15 se ve que el núcleo de un átomo es cerca de 100.000 veces menor que el átomo mismo, y sin embargo, concentra prácticamente el 100% de su masa.
Para efectos de comparación, si un átomo tuviese el tamaño de un estadio, el núcleo sería del tamaño de una canica colocada en el centro, y los electrones, como partículas de polvo agitadas por el viento alrededor de los asientos.
Evolución del modelo atómico
La concepción del átomo que se ha tenido a lo largo de la historia ha variado de acuerdo a los descubrimientos realizados en el campo de la física y la química. A continuación se hará una exposición de los modelos atómicos propuestos por los científicos de diferentes épocas. Algunos de ellos son completamente obsoletos para explicar los fenómenos observados actualmente, pero se incluyen a manera de reseña histórica.
Modelo de Dalton
Fue el primer modelo atómico con bases científicas, fue formulado en 1808 por John Dalton. Este primer modelo atómico postulaba:
- La materia está formada por partículas muy pequeñas llamadas átomos, que son indivisibles y no se pueden destruir.
- Los átomos de un mismo elemento son iguales entre sí, tienen su propio peso y cualidades propias. Los átomos de los diferentes elementos tienen pesos diferentes.
- Los átomos permanecen sin división, aún cuando se combinen en las reacciones químicas.
- Los átomos, al combinarse para formar compuestos guardan relaciones simples.
- Los átomos de elementos diferentes se pueden combinar en proporciones distintas y formar más de un compuesto.
- Los compuestos químicos se forman al unirse átomos de dos o más elementos distintos.
Sin embargo desapareció ante el modelo de Thomson ya que no explica los rayos catódicos, la radioactividad ni la presencia de los electrones (e-) o protones(p+).
Modelo de Thomson

Luego del descubrimiento del electrón en 1897 por Joseph John Thomson, se determinó que la materia se componía de dos partes, una negativa y una positiva. La parte negativa estaba constituida por electrones, los cuales se encontraban según este modelo inmersos en una masa de carga positiva a manera de pasas en un pastel (de la analogía del inglés plum-pudding model).
Detalles del modelo atómico
Para explicar la formación de iones, positivos y negativos, y la presencia de los electrones dentro de la estructura atómica, Thomson ideó un átomo parecido a un pastel de frutas. Una nube positiva que contenía las pequeñas partículas negativas (los electrones) suspendidos en ella. El número de cargas negativas era el adecuado para neutralizar la carga positiva. En el caso de que el átomo perdiera un electrón, la estructura quedaría positiva; y si ganaba, la carga final sería negativa. De esta forma, explicaba la formación de iones; pero dejó sin explicación la existencia de las otras radiaciones.
Modelo de Rutherford

Este modelo fue desarrollado por el físico Ernest Rutherford a partir de los resultados obtenidos en lo que hoy se conoce como el experimento de Rutherford en 1911. Representa un avance sobre el modelo de Thomson, ya que mantiene que el átomo se compone de una parte positiva y una negativa, sin embargo, a diferencia del anterior, postula que la parte positiva se concentra en un núcleo, el cual también contiene virtualmente toda la masa del átomo, mientras que los electrones se ubican en una corteza orbitando al núcleo en órbitas circulares o elípticas con un espacio vacío entre ellos. A pesar de ser un modelo obsoleto, es la percepción más común del átomo del público no científico. Rutherford predijo la existencia del neutrón en el año 1920, por esa razón en el modelo anterior (Thomson), no se habla de éste.
Por desgracia, el modelo atómico de Rutherford presentaba varias incongruencias:
- Contradecía las leyes del electromagnetismo de James Clerk Maxwell, las cuales estaban muy comprobadas mediante datos experimentales. Según las leyes de Maxwell, una carga eléctrica en movimiento (en este caso el electrón) debería emitir energía constantemente en forma de radiación y llegaría un momento en que el electrón caería sobre el núcleo y la materia se destruiría. Todo ocurriría muy brevemente.
- No explicaba los espectros atómicos.
Modelo de Bohr
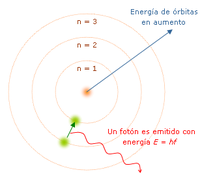
Este modelo es estrictamente un modelo del átomo de hidrógeno tomando como punto de partida el modelo de Rutherford, Niels Bohr trata de incorporar los fenómenos de absorción y emisión de los gases, así como la nueva mecánica cuántica desarrollada por Max Planck y el fenómeno del efecto fotoeléctrico observado por Albert Einstein.
“El átomo es un pequeño sistema solar con un núcleo en el centro y electrones moviéndose alrededor del núcleo en orbitas bien definidas.” Las orbitas están cuantizadas (los e- pueden estar solo en ciertas orbitas)
- Cada orbita tiene una energía asociada. La más externa es la de mayor energía.
- Los electrones no radian energía (luz) mientras permanezcan en orbitas estables.
- Los electrones pueden saltar de una a otra orbita. Si lo hace desde una de menor energía a una de mayor energía absorbe un cuanto de energia (una cantidad) igual a la diferencia de energía asociada a cada orbita. Si pasa de una de mayor a una de menor, pierde energía en forma de radiación (luz).
El mayor éxito de Bohr fue dar la explicación al espectro de emisión del hidrogeno. Pero solo la luz de este elemento. Proporciona una base para el carácter cuántico de la luz, el fotón es emitido cuando un electrón cae de una orbita a otra, siendo un pulso de energía radiada. Bohr no puede explicar la existencia de orbitas estables y para la condición de cuantización. Bohr encontró que el momento angular del electrón es h/2π por un método que no puede justificar.
Modelo de Schrödinger: modelo actual

Después de que Louis-Victor de Broglie propuso la Dualidad onda-corpúsculo en 1924, la cual fue generalizada por Schrödinger en 1926, se actualizó nuevamente el modelo del átomo.
En el modelo de Schrödinger se abandona la concepción de los electrones como esferas diminutas con carga que giran en torno al núcleo, que es una extrapolación de la experiencia a nivel macroscópico hacia las diminutas dimensiones del átomo. En vez de esto, Schrödinger describe a los electrones por medio de una función de onda, el cuadrado de la cual representa la probabilidad de presencia en una región delimitada del espacio. Esta zona de probabilidad se conoce como orbital.
Protón, electrón y neutrón
Protón
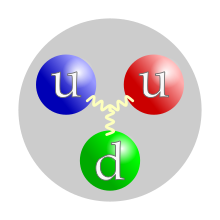
En física, el protón (en griego protón significa primero) es una partícula subatómica con una carga eléctrica de una unidad fundamental positiva
(+)(1,602 x 10–19 culombios) y una masa de 938,3 MeV/c2 (1,6726 × 10–27 kg) o, del mismo modo, unas 1836 veces la masa de un electrón. Experimentalmente, se observa el protón como estable, con un límite inferior en su vida media de unos 1035 años, aunque algunas teorías predicen que el protón puede desintegrarse. El protón y el neutrón, en conjunto, se conocen como nucleones, ya que conforman el núcleo de los átomos.
El núcleo del isótopo más común del átomo de hidrógeno (también el átomo estable más simple posible) es un único protón. Los núcleos de otros átomos están compuestos de nucleones unidos por la fuerza nuclear fuerte. El número de protones en el núcleo determina las propiedades químicas del átomo y qué elemento químico es.
Los protones están clasificados como bariones y se componen de dos quarks arriba y un quark abajo, los cuales también están unidos por la fuerza nuclear fuerte mediada por gluones. El equivalente en antimateria del protón es el antiprotón, el cual tiene la misma magnitud de carga que el protón, pero de signo contrario.
Debido a que la fuerza electromagnética es muchos órdenes de magnitud más fuerte que la fuerza gravitatoria, la carga del protón debe ser opuesta e igual (en valor absoluto) a la carga del electrón; en caso contrario, la repulsión neta de tener un exceso de carga positiva o negativa causaría un efecto expansivo sensible en el universo, y, asimismo, en cualquier cúmulo de materia (planetas, estrellas, etc.).
Neutrón
Un neutrón es una variación neutra formada por dos quarks down y un quark up. Forma, junto con los protones, los núcleos atómicos. Fuera del núcleo atómico es inestable y tiene una vida media de unos 15 minutos emitiendo un electrón y un antineutrino para convertirse en un protón. Su masa es muy similar a la del protón.
Algunas de sus propiedades:
- Masa: mn = 1,6749x10-27 Kg = 1,008587833 uma
- Vida media: tn = 886,7 ± 1,9s
- Momento magnético: mn = -1,9130427 ± 0,0000005 mN
El neutrón es necesario para la estabilidad de casi todos los núcleos atómicos (la única excepción es el hidrógeno), ya que interactúa fuertemente atrayéndose con los protones, pero sin repulsión electrostática.
Protón Estructura de quarks de un protón.
En física, el protón (en griego protón significa primero) es una partícula subatómica con una carga eléctrica de una unidad fundamental positiva (+)(1,602 x 10–19 culombios) y una masa de 938,3 MeV/c2 (1,6726 × 10–27 kg) o, del mismo modo, unas 1836 veces la masa de un electrón. Experimentalmente, se observa el protón como estable, con un límite inferior en su vida media de unos 1035 años, aunque algunas teorías predicen que el protón puede desintegrarse. El protón y el neutrón, en conjunto, se conocen como nucleones, ya que conforman el núcleo de los átomos.
El núcleo del isótopo más común del átomo de hidrógeno (también el átomo estable más simple posible) es un único protón. Los núcleos de otros átomos están compuestos de nucleones unidos por la fuerza nuclear fuerte. El número de protones en el núcleo determina las propiedades químicas del átomo y qué elemento químico es.
Los protones están clasificados como bariones y se componen de dos quarks arriba y un quark abajo, los cuales también están unidos por la fuerza nuclear fuerte mediada por gluones. El equivalente en antimateria del protón es el antiprotón, el cual tiene la misma magnitud de carga que el protón, pero de signo contrario.
Debido a que la fuerza electromagnética es muchos órdenes de magnitud más fuerte que la fuerza gravitatoria, la carga del protón debe ser opuesta e igual (en valor absoluto) a la carga del electrón; en caso contrario, la repulsión neta de tener un exceso de carga positiva o negativa causaría un efecto expansivo sensible en el universo, y, asimismo, en cualquier cúmulo de materia (planetas, estrellas, etc.). Neutrón
Un neutrón es una variación neutra formada por dos quarks down y un quark up. Forma, junto con los protones, los núcleos atómicos. Fuera del núcleo atómico es inestable y tiene una vida media de unos 15 minutos emitiendo un electrón y un antineutrino para convertirse en un protón. Su masa es muy similar a la del protón.
Algunas de sus propiedades:
Masa: mn = 1,6749x10-27 Kg = 1,008587833 uma Vida media: tn = 886,7 ± 1,9s Momento magnético: mn = -1,9130427 ± 0,0000005 mN
El neutrón es necesario para la estabilidad de casi todos los núcleos atómicos (la única excepción es el hidrógeno), ya que interactúa fuertemente atrayéndose con los protones, pero sin repulsión electrostática. Electrón Electrón Los primeros orbitales inferiores de átomos de hidrógeno mostradas como secciones transversales con código de color que muestra la probabilidad de densidad. Clasificación Partículas elementales Fermión Lepton Primera generación Electrón Propiedades Masa: 9.1094 × 10−31kg ¹⁄1836uma Carga eléctrica: −1.6 × 10−19C Spin: ½ Color de carga: Interacción: Interacción gravitatoria, Interacción electromagnética, Interacción débil
El electrón (Del griego ελεκτρον, ámbar), comúnmente representado como e−) es una partícula subatómica de tipo fermiónico. En un átomo los electrones rodean el núcleo atómico, compuesto fundamentalmente de protones y neutrones.
Los electrones tienen una masa pequeña respecto al protón, y su movimiento genera corriente eléctrica en la mayoría de los metales. Estas partículas desempeñan un papel primordial en la química ya que definen las atracciones con otros átomos.== Electrón == {
Escala física de los pesos atómicos
Física/Física moderna/Escala física de los pesos atómicos
El núcleo atómico
Física/Física moderna/El núcleo atómico
La estructura electrónica
Física/Física moderna/La estructura electrónica
Espectros
Física/Física moderna/Espectros
Modelo atómico de Bohr

Niels Bohr se basó en el átomo de hidrógeno para realizar el modelo que lleva su nombre. Bohr intentaba realizar un modelo atómico capaz de explicar la estabilidad de la materia y los espectros de emisión y absorción discretos que se observan en los gases.
Describió el átomo de hidrógeno con un protón en el núcleo, y girando a su alrededor un electrón.
El modelo atómico de Bohr partía conceptualmente del modelo atómico de Rutherford y de las incipientes ideas sobre cuantización que habían surgido unos años antes con las investigaciones de Max Planck y Albert Einstein. Debido a su simplicidad el modelo de Bohr es todavía utilizado frecuentemente como una simplificación de la estructura de la materia.
Características
En este modelo los electrones giran en órbitas circulares alrededor del núcleo, ocupando la órbita de menor energía posible, o sea la órbita más cercana al núcleo posible.
El electromagnetismo clásico predecía que una partícula cargada moviéndose de forma circular y envontrado con un cuadrado el cual emitiría energía por lo que los electrones deberían colapsar sobre el núcleo en breves instantes de tiempo. Para superar este problema Bohr supuso que los electrones solamente se podían mover en órbitas específicas, cada una de las cuales caracterizada por su nivel energético. Cada órbita puede entonces identificarse mediante un número entero n que toma valores desde 1 en adelante. Este número "n" recibe el nombre de Número Cuántico Principal.
Bohr supuso además que el momento angular de cada electrón estaba cuantizado y sólo podía variar en fracciones enteras de la constante de Planck. De acuerdo al número cuántico principal calculó las distancias a las cuales se hallaba del núcleo cada una de las órbitas permitidas en el átomo de hidrógeno.
Estos niveles en un principio estaban clasificados por letras que empezaban en la "K" y terminaban en la "Q". Posteriormente los niveles electrónicos se ordenaron por números. Cada órbita tiene electrones con distintos niveles de energía obtenida que después se tiene que liberar y por esa razón el electrón va saltando de una órbita a otra hasta llegar a una que tenga el espacio y nivel adecuado, dependiendo de la energía que posea, para liberarse sin problema y de nuevo volver a su órbita de origen.
El modelo atómico de Bohr constituyó una de las bases fundamentales de la mecánica cuántica. Explicaba la estabilidad de la materia y las características principales del espectro de emisión del hidrógeno. Sin embargo no explicaba el espectro de estructura fina que podría ser explicado algunos años más tarde gracias al modelo atómico de Sommerfeld. Históricamente el desarrollo del modelo atómico de Bohr junto con la dualidad onda-corpúsculo permitiría a Erwin Schrödinger descubrir la ecuación fundamental de la mecánica cuántica.
Postulados de Bohr
En 1913 Niels Bohr desarrolló su célebre modelo atómico de acuerdo a 4 postulados fundamentales:
- Los electrones orbitan en el átomo en niveles discretos y cuantizados de energía, es decir, no todas las órbitas están permitidas, tan sólo un número finito de éstas.
- Los electrones pueden saltar de un nivel electrónico a otro sin pasar por estados intermedios.
- El salto de un electrón de un nivel cuántico a otro implica la emisión o absorción de un único cuanto de luz (fotón) cuya energía corresponde a la diferencia de energía entre ambas órbitas.
- Las órbitas permitidas tienen valores discretos o cuantizados del momento angular orbital L de acuerdo con la siguiente ecuación:
- Donde n = 1,2,3,… es el número cuántico angular o número cuántico principal.
La cuarta hipótesis asume que el valor mínimo de n es 1. Este valor corresponde a un mínimo radio de la órbita del electrón de 0.0529 nm. A esta distancia se le denomina radio de Bohr. Un electrón en este nivel fundamental no puede descender a niveles inferiores emitiendo energía. Se puede demostrar que este conjunto de hipótesis corresponde a la hipótesis de que los electrones estables orbitando un átomo están descritos por funciones de onda estacionarias.
Otras partículas elementales
Física/Física moderna/Otras partículas elementales
Desintegración radiactiva
Física/Moderna/Desintegración radiactiva
Núcleos inestables
Los núcleos inestables son aquellos que emiten radiación sin razón aparente. Estos núcleos emiten partículas debido a que es la única forma en que pueden adquirir estabilidad.
Tipos de radiación natural
Física/Moderna/Desintegración radiactiva/Tipos de radiación natural
Leyes del desplazamiento radiactivo
Física/Moderna/Desintegración radiactiva/Leyes del desplazamiento radiactivo
Constantes radiactivas
Física/Moderna/Desintegración radiactiva/Constantes radiactivas
Radiactividad artificial
Física/Moderna/Desintegración radiactiva/Radiactividad artificial
Detección de la radiación
Física/Moderna/Desintegración radiactiva/Detección de la radiación
Unidades de medida de la radiactividad
Física/Moderna/Desintegración radiactiva/Unidades de medida de la radiactividad
Dosis de radiación
Física/Moderna/Desintegración radiactiva/Dosis de radiación
Radiación cósmica
Física/Moderna/Desintegración radiactiva/Radiación cósmica
Alcance de la radiación
Física/Moderna/Desintegración radiactiva/Alcance de la radiación
Reacciones nucleares
Física/Moderna /Reacciones nucleares
Concepto de sección eficaz
Física/Moderna /Reacciones nucleares/Concepto de sección eficaz
Aceleradores de partículas
Física/Moderna /Reacciones nucleares/Aceleradores de partículas
Reacciones nucleares provocadas por neutrones
Física/Moderna /Reacciones nucleares/Reacciones nucleares provocadas por neutrones
La fisión nuclear
La fisión nuclear es la ruptura de un atomo para formar dos o mas especies. este fenomeno es el mas conocido. un nucleo pesado como el uranio enrriquecido se bombardea con particulas para romper su nucleo con la consecuente liberacion de energia y particulas subatomicas. (ARP)
Producción de isótopos
Física/Moderna /Reacciones nucleares/Producción de isótopos
La fusión nuclear
La fusion nuclear es la combinacion de dos o mas nucleos de atomos para formar una especie nueva. por ejemplo la formacion de helio a partir de dos nucleos de hidrogeno. Este fenomeno es el que se lleva a cabo en el sol. (ARP)
Masa y energía
Se consideraba a la masa y a la energia como entidades totalmente diferentes hasta que Einstein lo cambio con su famosa relacion E= mc2; donde E es la energia, m es la masa y c es la velocidad de la luz al cuadrado. Con lo que se establece que la masa y la energia son iguales y sienta las bases de la fisica nuclear.
Dado que la destruccion de la masa conlleva la generacion de una enorme cantidad de energia. (ARP)
Apéndices
Ejercicios de Física General
Aqui encontrarás una variedad de ejercicios de exámenes resueltos de Física..
pilas son los exámenes tomados en una de las mejores universidades del Ecuador
http://www.icf.espol.edu.ec/index.php?view=article&catid=36%3ARecursos&id=77%3AEx%C3%A1menes&Itemid=82&option=com_content (EL ENLACE YA NO ESTA DISPONIBLE)
también podrás encontrar deberes y muchos recursos que te servirán
Teoria de la Relatividad
Física/Teoria de la Relatividad




































































![{\displaystyle \varphi \left(t\right)=\int _{0}^{t}{\omega \,\operatorname {d} t}=\int _{0}^{t}{\left[{\int _{0}^{t}{\alpha \,\operatorname {d} t}}\right]}\operatorname {d} t\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f88051e114316d650fb4fd419d2f83eac12c73e1)




![{\displaystyle {\begin{aligned}{\overrightarrow {r}}\,\cdot {\overrightarrow {v}}&=r\left({\cos \omega \,t}\right)\left[-r\omega \left({\sin \omega \,t}\right)\right]+r\left({\sin \omega \,t}\right)r\omega \left({\cos \omega \,t}\right)\\&=-r^{2}\omega \left({\sin \omega \,t}\right)\left({\cos \omega \,t}\right)+r^{2}\omega \left({\sin \omega \,t}\right)\left({\cos \omega \,t}\right)\\&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2452256307901ce1a7b53b4592a6da7b29915a0e)





![{\displaystyle {\overrightarrow {v}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}=r\alpha \,t\left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]=r\omega \left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610a2564823b8defefeeecbe611e585aca6af86a)
![{\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}=r\alpha \left[{-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f27d7325d8770cf13ee8446c138f086d328e25d8)
![{\displaystyle +\,r\alpha ^{2}t^{2}\left[{\left({-\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85262543608f244520a74930287c29b567f7430)
![{\displaystyle {\overrightarrow {a}}=\left[{-r\alpha \left({\sin \varphi }\right)-r\omega ^{2}\left({\cos \varphi }\right)}\right]{\overrightarrow {i}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5796d2f39e4a3a173a01ac6885e4fd4703696c98)
![{\displaystyle +\left[{r\alpha \left({\cos \varphi }\right)-r\omega ^{2}\left({\sin \varphi }\right)}\right]{\overrightarrow {j}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f61d1f3b5ba7920a08d07a4d4628620cad7e77e3)


































































































































































































































































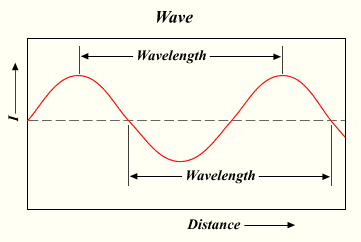

























































































![{\displaystyle L_{f}=L_{0}[1+\alpha _{L}(T_{f}-T_{0})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/097fa172836b860d72f6ff2bfa0d8347c15d9f24)













































































































































































![{\displaystyle W=-\int _{A}^{B}\kappa {\frac {q_{1}\cdot q_{2}}{r^{2}}}\cdot dr=\left[\kappa {\frac {q_{1}\cdot q_{2}}{r}}\right]_{r_{A}}^{r_{B}}=\kappa {\frac {q_{1}\cdot q_{2}}{r_{B}}}-\kappa {\frac {q_{1}\cdot q_{2}}{r_{A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d21aa2aca990569d29a15280cad3f9419e04522)
![{\displaystyle W=\int _{\infty }^{r}\kappa {\frac {q_{1}\cdot q_{2}}{r^{2}}}\cdot dr=\left[\kappa {\frac {q_{1}\cdot q_{2}}{r}}\right]_{\infty }^{r}=\kappa {\frac {q_{1}\cdot q_{2}}{r}}-\kappa {\frac {q_{1}\cdot q_{2}}{r_{A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d06ec4734a1f6792fe2ad7007fc1ae8e2a749bbc)













































































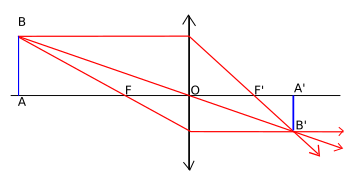

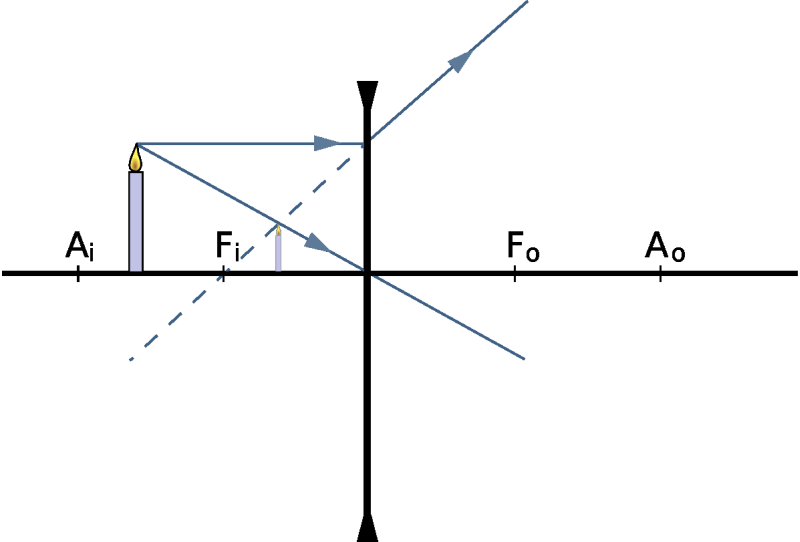

![{\displaystyle \displaystyle \psi '[D]={\frac {1}{f'[m]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47483600b6b3c94fed105067e4cc5e8ad564aff1)


































































