Administración de empresas/Estadística para los negocios/Prueba de hipótesis (estadística)

PRUEB

A DE HIPÓTESIS (ESTADÍSTICA)

Administración de empresas Proyecto de Aprendizaje Herramientas

Índice de contenidos

Datos bibliográficos (dar click para más información)
D. MURA, JOSEPH Administración: Una aproximación íntegra Estadística para los negocios Prueba de hipótesis (estadística) 2015 En: https://es.wikibooks.org/wiki/Administración_de_empresas FUNDACIÓN WIKIMEDIA - PROYECTO WIKILIBROS, bajo licencia CC BY-SA 3.0

Esta obra está bajo la licencia CC BY-SA 3.0
(dar click para más información)

Esta obra está bajo la licencia CC BY-SA 3.0

Usted es libre de:

Compartir — copiar y redistribuir el material en cualquier medio o formato

Adaptar — remezclar, transformar y crear a partir del material para cualquier finalidad, incluso comercial.

Bajo las condiciones siguientes:

Reconocimiento — Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.

CompartirIgual — Si remezcla, transforma o crea a partir del material, deberá difundir sus contribuciones bajo la misma licencia que el original.

Administración de empresas/Estadística para los negocios/Índice de contenidos

Los principios tratados en este recuadro representan a los principios por los cuales se guía el libro. Aunque no se mencionen explícitamente en cada parte, se encuentran, aún así, ímplicitos.

La administración depende del contexto.
El recurso más valioso es el tiempo.
Las personas no son un recurso.
El éxito no es alcanzable directamente, o sea, no se puede pretender alcanzarlo mediante un plan de acción o la consecución de esfuerzos; sino que puede nacer o no como consecuencia de los resultados hechos o nuestras acciones.

Para pruebas de hipótesis con valores cualitativos ver: Prueba χ² (Chi-cuadrado)

Es un procedimiento estadístico que permite aceptar o rechazar una afirmación hecha con respecto a una cantidad cuantitativa de datos determinada.

El procedimiento consta de seis (6) pasos.

Hipótesis estadísticas

Se les denomina así a los supuestos (hipótesis) realizados con respecto a un parámetro o estadístico (media, proporción, entre otros).

En este paso se definen dos tipos de hipótesis:

H_o: Hipótesis nula
H₁: Hipótesis alterna (de la cual se sospecha pudiera ser cierta, es planteada por el investigador)

Planteamiento con una variable

Este tipo de desarrollo va de la forma: "¿Se podría afirmar que el promedio de tiempo que se demora una persona en vestirse es de 10 minutos?".

En el cual se desea averiguar de una variable si la cantidad inducida es correcta o falsa.

Dependiendo de cómo se plantee la incógnita, se pueden distinguir tres casos:

CASO I	CASO II	CASO III
*H_o: U = 10 min *H₁: U ≠ 10 min	*H_o: U = 10 min *H₁: U > 10 min	*H_o: U = 10 min *H₁: U < 10 min
El tiempo promedio que se demora una persona en vestirse no es igual o es diferente a 10 minutos	El tiempo promedio que se demora una persona en vestirse es más o superior a 10 minutos	El tiempo promedio que se demora una persona en vestirse es menos o inferior a 10 minutos

Planteamiento con dos variables o por comparación

Este tipo de desarrollo va de la forma: "¿Se podría afirmar que las ganancias de las empresas medianas han crecido este año con respecto al año anterior?".

En el cual se compara un valor predefinido con respecto a una suposición entre una variable con otra variable para determinar si esta es correcta o falsa.

Dependiendo de cómo se plantee la incógnita, se pueden distinguir tres casos:

CASO I	CASO II	CASO III
*H_o: U₁ = U₂ *H₁: U₁ ≠ U₂	*H_o: U₁ = U₂ *H₁: U₁ > U₂	*H_o: U₁ = U₂ *H₁: U₁ < U₂
Las ganancias de las empresas medianas en este año no son iguales o son diferentes al año anterior	Las ganancias de las empresas medianas en este año son más o superiores al año anterior	Las ganancias de las empresas medianas en este año son menos o inferiores al año anterior

Nivel de significancia (α)

Se le conoce así al error máximo adoptado al momento de rechazar la hipótesis nula (H_o) cuando es verdadera.

Dependiendo del tipo de de significación que se da al estudio, hay tres grados:

α = 0.01 → Muy significativo o de significación del 1%
α = 0.05 → Significativo o de significación del 5%
α = 0.10 → Poco significativo o de significación del 10% (rara vez usado)

Valor de la distribución 'Z' o 't'

En este paso se procede a ubicar el intervalo de confianza para poder rechazar o aceptar H_o.

Hay dos formas de encontrar dicho valor: mediante la tabla " Z " o la tabla " t ".

Para definir cuál es la tabla en la que se buscará la información, se debe de considerar el número de datos con los que se cuenta.

Si la cantidad de datos sobrepasa o es igual a 30, se usará la tabla " Z "
Si la cantidad de datos es menor a 30, se usará la tabla " t ".

Ejemplo:

"De una muestra de 30 alumnos..." - Se usa la tabla Z.

"Se encuestó a 14 personas..." - Se usa la tabla t.

Determinar el intervalo de confianza

El intervalo de confianza es el punto que separa a la Región de Aceptación y Rechazo.

Una variable

Tabla Z

Véase: Tabla de la distribución Z para valores de este tipo

Para hallar el intervalo en esta tabla se sigue la siguiente fórmula:

$Z=\alpha$
Donde: α = Nivel de significancia
Ejemplo: Nivel de significancia del 1 % $Z=0.01(000)$ Se procede a buscar el valor en la tabla Z 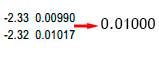tabla z ejemplo Y se toma el valor más cercano al que buscamos. $0.00990->Z=-2.33$

Tabla t

Véase: Tabla de la distribución t para valores de este tipo

Para hallar el intervalo en la tabla t-student se sigue la siguiente fórmula:

Para cuando H1 es " < " o " > "	Para cuando H1 es " ≠ "
$t=(n-1),({\frac {\alpha }{1}})$	$t=(n-1),({\frac {\alpha }{2}})$
Donde: α = Nivel de significancia n = Cantidad de datos	Donde: α = Nivel de significancia n = Cantidad de datos
Ejemplo: Nivel de significancia del 1 % con 22 datos $t=(22-1),({\frac {0.01}{1}})$ $t=21,0.01$ Se procede a buscar el valor en la tabla t $t=2.518$	Ejemplo: Nivel de significancia del 1 % con 22 datos $t=(22-1),({\frac {0.01}{2}})$ $t=21,0.005$ Se procede a buscar el valor en la tabla t $t=2.831$

Dos variables

Tabla Z

Véase: Tabla de la distribución Z para valores de este tipo

Para hallar el intervalo en esta tabla se sigue la siguiente fórmula:

Para usar esta fórmula, por lo menos n₁ o n₂ tienen que tener un valor mayor o igual a 30

n₁ ≥ 30
n₂ ≥ 30

$Z=\alpha$
Donde: α = Nivel de significancia
Ejemplo: Nivel de significancia del 1 % con 34 (n₁) y 65 (n₂) datos $n_{1}\geq 34$ $n_{2}\geq 65$ Como ambos datos son mayores o iguales a 30, se realiza el procedimiento habitual $Z=0.01(000)$ Se procede a buscar el valor en la tabla Z tabla z ejemplo Y se toma el valor más cercano al que buscamos. $0.00990->Z=-2.33$

Tabla t

Véase: Tabla de la distribución t para valores de este tipo

Para hallar el intervalo en la tabla t-student se sigue la siguiente fórmula:

Para usar esta fórmula, tanto n₁ como n₂ tienen que tener un valor inferior a 30

n₁ < 30
n₂ < 30

$t=(n_{1}+n_{2}-2),({\frac {\alpha }{1}})$	$t=(n_{1}+n_{2}-2),({\frac {\alpha }{2}})$
Donde: α = Nivel de significancia n = Cantidad de datos	Donde: α = Nivel de significancia n = Cantidad de datos
Ejemplo: Nivel de significancia del 1 % con 10 (n₁) y 7 (n₂) datos $n_{1}\geq 10$ $n_{2}\geq 7$ Como ambos datos son mayores o iguales a 30, se realiza el procedimiento habitual $t=(10+7-2),({\frac {0.01}{1}})$ $t=15,0.01$ Se procede a buscar el valor en la tabla t $t=2.602$	Ejemplo: Nivel de significancia del 1 % con 10 (n₁) y 7 (n₂) datos $n_{1}\geq 10$ $n_{2}\geq 7$ Como ambos datos son mayores o iguales a 30, se realiza el procedimiento habitual $t=(10+7-2),({\frac {0.01}{2}})$ $t=15,0.005$ Se procede a buscar el valor en la tabla t $t=2.947$

Estadístico de prueba 'Z' o 't'

Se le conoce como Estadístico de Prueba al valor que resulta luego de aplicar una determinada fórmula a la información de la muestra tomada y que se utiliza para rechazar o aceptar la Hipótesis Nula (H_o) a través del Valor de la Distribución.

A continuación se muestran fórmulas detalladas para cada tipo de caso:

Una media o promedio

Para muestras mayores o igual a 30

$Z={\frac {{\bar {X}}-u}{\sqrt {\frac {\sigma ^{2}}{n}}}}$

Donde:

${\bar {X}}$ = Promedio parcial (de la muestra)
$\sigma$ = Desviación poblacional total
$u$ = Valor de la hipótesis
$n$ = Número de datos

Para muestras menores a 30

$t={\frac {{\bar {X}}-u}{\sqrt {\frac {S}{n}}}}$

Donde:

${\bar {X}}$ = Promedio parcial (de la muestra)
$S$ = Desviación de la muestra
$u$ = Valor de la hipótesis
$n$ = Número de datos

Una proporción o porcentaje

Para muestras mayores o igual a 30

$Z={\frac {{\hat {P}}-P_{0}}{\frac {P_{0}(1-P_{0})}{n}}}$

Donde:

${\hat {P}}$ = Proporción de la muestra

Se puede conseguir de la siguiente forma, si el problema no lo da

{\hat {P}}={\frac {X}{n}}

$X$ = Valor numérico de la muestra
$P_{0}$ = Proporción poblacional (total)
$n$ = Número de datos

Para muestras menores a 30

$t={\frac {{\hat {P}}-P_{0}}{\frac {{\hat {P}}(1-{\hat {P}})}{n}}}$

Donde:

${\hat {P}}$ = Proporción de la muestra

Se puede conseguir de la siguiente forma, si el problema no lo da

{\hat {P}}={\frac {X}{n}}

$X$ = Valor numérico de la muestra
$P_{0}$ = Proporción poblacional (total)
$n$ = Número de datos

Diferencia de dos medias o promedios

$Z={\frac {({\bar {X_{1}}}-{\bar {X_{2}}})-({\bar {U_{1}}}-{\bar {U_{2}}})}{\sqrt {{\frac {\sigma _{1}^{2}}{n_{1}}}+{\frac {\sigma _{2}^{2}}{n_{2}}}}}}$

Donde:

${\bar {X}}_{1}$ = Promedio de la primera variable
${\bar {X}}_{2}$ = Promedio de la segunda variable
${\bar {U}}_{1}$ = Porcentaje de la primera variable (si no se especifica es 100 (%))
${\bar {U}}_{2}$ = Porcentaje de la segunda variable (si no se especifica es 100 (%))
$\sigma _{1}$ = Desviación de la primera variable
$\sigma _{2}$ = Desviación de la segunda variable
$n_{1}$ = Número de datos de la primera variable(total)
$n_{2}$ = Número de datos de la segunda variable(total)

Diferencia de proporciones o porcentajes

$Z={\frac {({\hat {U_{1}}}-{\hat {U_{2}}})-(U_{1}-U_{2})}{\sqrt {[U(1-U)]\quad ({\frac {1}{n_{1}}}+{\frac {1}{n_{2}}})}}}$

donde:

$U={\frac {X_{1}+X_{2}}{n_{1}+n_{2}}}$

Donde:

${\hat {U}}_{1}$ = Promedio de la primera variable en proporción (por ejemplo: 0.30)
${\hat {U}}_{2}$ = Promedio de la segunda variable en proporción

Se puede conseguir de la siguiente forma, si es un porcentaje

{\hat {U_{1}}}={\frac {X_{1}}{n_{1}}}

o

{\hat {U_{2}}}={\frac {X_{2}}{n_{2}}}

${\bar {X}}_{1}$ = Promedio de la primera variable en porcentaje (por ejemplo: 30 (%))
${\bar {X}}_{2}$ = Promedio de la segunda variable en porcentaje (por ejemplo: 30 (%))
$U_{1}$ = Porcentaje de la primera variable (si no se especifica es 100 (%))
$U_{2}$ = Porcentaje de la segunda variable (si no se especifica es 100 (%))
$n_{1}$ = Número de datos de la primera variable(total)
$n_{2}$ = Número de datos de la segunda variable(total)

Región de aceptación y rechazo

Una vez obtenidos los datos necesarios para poder realizar el procedimiento estadístico, se deberán de colocar en un gráfico que ilustre cómo se plantea; se determina si se acepta o se niega la hipótesis nula (H_o).

**Cuando...**
H₁: ≠	H₁: <	H₁: >
Área de aceptación y rechazo desigual	Área de aceptación y rechazo menor	Área de aceptación y rechazo mayor

Los valores se sustituyen por cada uno de los puntos mencionados en la gráfica correspondiente. Puede resultarte algo parecido a esto:

Nivel de significancia del 1 %, menos de 30 datos y cuando H₁ es mayor

En este caso se rechaza H_o, por lo que se acepta H₁

El Valor de la Distribución puede ir tanto en el lado negativo como en el positivo, su signo también se acomoda al lugar en el que se encuentra.

Nivel de significancia del 1 %, menos de 30 datos y cuando H₁ es desigual

En este caso se acepta H_o, por lo que se rechaza H₁

Decisión

Important icon

Los niveles de significancia deben ser reemplazado por su similar literal

α = 0.01 o de significación del 1% → Muy significativo
α = 0.05 o de significación del 5% → Significativo
α = 0.10 o de significación del 10% → Poco significativo(rara vez usado)

Es la parte final del procedimiento de prueba de hipótesis, en la que redactamos una conclusión de todo el estudio realizado.

Esta parte tiene que incluir necesariamente: El nivel de significancia, la inclusión de Ho ó H1 y su aceptación o rechazo.

Ejemplo de una plantilla de redacción:

Se puede afirmar muy significativamente que el número de personas que asisten al supermercado no ha aumentado.

Ejemplos según el gráfico:

Se rechaza H_o
Se puede afirmar significativamente que el número de personas que asisten al supermercado ha disminuido

Se acepta H_o
Se puede afirmar significativamente que el número de personas que asisten al supermercado no ha cambiado