1.4.1 Si  e
e  son dos conjuntos cualesquiera, la diferencia de
son dos conjuntos cualesquiera, la diferencia de  e
e  es el conjunto
es el conjunto  (también simbolizado por
(también simbolizado por  ) definido por
) definido por
 y
y  .
.
Es decir,  consiste de todos los elementos que están en
consiste de todos los elementos que están en  pero no en
pero no en  . Este conjunto se representa por el área sombreada en el siguiente diagrama:
. Este conjunto se representa por el área sombreada en el siguiente diagrama:
 Diferencia de
Diferencia de  e
e  , o entre A y B en este caso
, o entre A y B en este caso
Ejercicio: Probar que  e
e  son conjuntos disjuntos si y solo si
son conjuntos disjuntos si y solo si  .
.
Sean  ,
,  y
y  conjuntos cualesquiera. Entonces
conjuntos cualesquiera. Entonces
( D-1 ) 
( D-2 ) 
( D-3 ) 
( D-4 ) 
( D-5 ) 
( D-6 ) 
( D-7 ) 
( D-8 )  si y solo si
si y solo si 
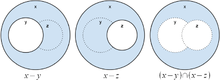 Ver diagrama
Ver diagrama
1.4.2. Si  es un subconjunto de
es un subconjunto de  , entonces el subconjunto de
, entonces el subconjunto de  ,
,
 ,
,
se dice conjunto complementario de  en
en  . En el siguiente diagrama se representa este conjunto como el area sombreada:
. En el siguiente diagrama se representa este conjunto como el area sombreada:
 Complemento de
Complemento de  en
en  , o de A en U en este caso
, o de A en U en este caso
Sean  e
e  subconjuntos de un conjunto
subconjuntos de un conjunto  . Se cumplen
. Se cumplen
( C-1 ) 
( C-2 ) 
( C-3 )  (conmutatividad)
(conmutatividad)
( C-4 ) 
( C-5 ) 
( C-6 ) 
( C-7 ) 
( C-8 ) 
( C-9 ) 
Los enunciados ( C-7 ) y ( C-8 ) se conocen como leyes de De Morgan.
1.4.3. En ocasiones, para evitar complejidades notacionales, escribiremos  en lugar de
en lugar de  cuando del contexto se sobreentienda cual es el conjunto
cuando del contexto se sobreentienda cual es el conjunto  .
.
Capítulo anterior: Unión e intersección de conjuntos
Capítulo siguiente: Conjuntos potencia



































