Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Lunar/Teoría de los Eclipses Lunares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Teoría de los Eclipses Lunares y Cálculo de los Elementos Besselianos
editarOcurrencia de un Eclipse Lunar
editarHabiendo hallado por interpolación [1] a β (1), siendo la distancia angular en [°] desde el centro de la Luna al centro del Cono de la Sombra Terrestre (Umbra) en la Oposición (Ascensiones Rectas del Sol y de la Luna exactamente opuestas) [2] es decir en la Sizigia (fase lunar llena) y también hallado su instante, se procede determinar que tipo de Eclipse Lunar ocurre según las siguientes condiciones:
Para los Eclipses Lunares con la Umbra:
- Si β < 0,89165277777 entonces hay con seguridad un Eclipse Lunar Parcial o Total (Umbra).
- Si 0,89165277777 <= β <= 1,06363333333 entonces hay dudas si hay un Eclipse Lunar Parcial o Total (Umbra).
- Si β > 1,06363333333 entonces no hay un Eclipse Lunar Parcial o Total (Umbra).
Para los Eclipses Lunares con la Penumbra:
- Si β < 1,44471944444 entonces hay con seguridad un Eclipse Lunar Parcial o Total (Penumbral).
- Si 1,44471944444 <= β <= 1,60763333333 entonces hay dudas si hay un Eclipse Lunar Parcial o Total (Penumbral).
- Si β > 1,60763333333 entonces no hay un Eclipse Lunar Parcial o Total (Penumbral).
Contactos Exteriores e Interiores de la Luna con la Penumbra y la Umbra
editar
Contactos Exteriores e Interiores de la Luna con la Penumbra en E y en I.
Contactos Exteriores e Interiores de la Luna con la Umbra en F y en H.
El Eclipse Máximo ocurrirá cuando la Luna esté en o muy próxima a G.
Vp es el vértice del Cono Penumbral de la Tierra.
Vu es el vértice del Cono de la Sombra (Umbra) de la Tierra.
(*) Los astros y sus distancias no están a escala.
Ecuaciones Fundamentales y Cálculos de los Elementos Besselianos. Ejemplos prácticos según el Eclipse Lunar Total del 21.01.2019
editarEfemérides de la Luna y del Sol
editarSabiendo que la Oposición Sol-Luna, en Ascensión Recta, ocurre a las 05:13:08 hs. (GMT = Greenwich Meridian Time) [1] tomamos 7 horas para los cálculos respectivos. T₀ = 5 hs. es la hora central y anterior más cercana a tal oposición, luego se realizan los cálculos para ±3 hs. a partir de esa T₀, es decir para las 2 hs., 3 hs., 4 hs., 5 hs., 6 hs., 7 hs. y 8 hs. (GMT).
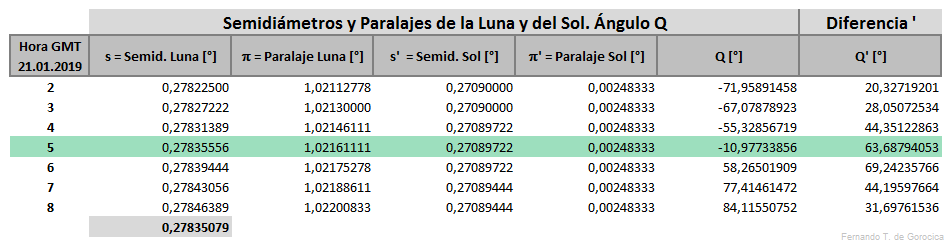
Ambos astros están en Coordenadas Ecuatoriales Geocéntricas tomadas de las Efemérides diarias (00:00 GMT), y publicadas, por ejemplo, por The Astonomical Almanac donde las Ascensiones Rectas (α) de la Luna y las del Sol están en el formato Hora, Minutos y Segundos, y las Declinaciones (δ) de la Luna y las del Sol en el formato °, ' y ". También desde estas efemérides se toman la Paralaje Ecuatorial Horizontal de la Luna π en [°], el semidiámetro s de la Luna en [°], la Paralaje Ecuatorial Horizontal del Sol π' en [°] y el semidiámetro s' del Sol en [°]. Observar que se mantienen casi constantes en las 7 horas.
Calcular Q en [°] que es la distancia angular desde el centro de la Luna al centro de la Umbra (cono de sombra terrestre) en el instante dado, entonces
- Q = Atan(Cos(δ) * Seno(α - α') / (Cos(δ') * Seno(δ) + Seno(δ') * Cos(δ) * Cos(α - α'))) (2) [3]
siendo negativo (-) antes de la Oposición (en Ascensión Recta, Q = 0°) y positivo (+) luego de la misma.
Primer y Último contacto Exterior e Interior de la Luna con la Penumbra y la Umbra
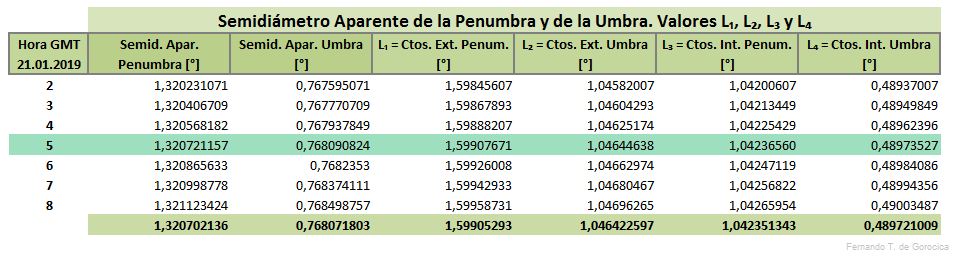
editarCalcular primero el Semidiámetro aparente de la Penumbra en [°]
- Semid. Penumbra = 1,02 * (0,99983652982 * π + s' + π') (3)
Luego el Semidiámetro aparente de la Umbra en [°]
- Semid. Umbra = 1,02 * (0,99983652982 * π - s' + π') + s (4)
Para el Primer y Último Contacto Exterior de la Luna con la Penumbra en [°], calcular
- L₁ = 1,02 * (0,99983652982 * π + s' + π') + s (5)
Para el Primer y Último Contacto Exterior de la Luna con la Umbra en [°], calcular
- L₂ = 1,02 * (0,99983652982 * π - s' + π') + s (6)
Para el Primer y Último Contacto Interior de la Luna con la Penumbra en [°], calcular
- L₃ = 1,02 * (0,99983652982 * π + s' + π') - s (7)
Para el Primer y Último Contacto Interior de la Luna con la Umbra en [°], calcular
- L₄ = 1,02 * (0,99983652982 * π - s' + π') - s (8)
En todos los 6 casos se tomará el promedio para los cálculos posteriores.
Cálculo de los valores ε, x e y
editarCalcular ε, x e y todos en ["]
- ε = ((Seno(2 * δ') * (Seno((α - α' + 180) * 1800))^2) / Seno(1)) (9)
- x = (α - α' + 180) * Cos(δ) * 3600 (10)
- y = (δ + δ') * 3600 - ε (11)
Los incrementos horarios de x y de y, es decir x' e y', se hallarán sacando el promedio en las columnas "diferencias" según la siguiente tabla:
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de un Eclipse Lunar |
| 01 | 02 | 03 |
| 04 |
Notas de referencia
editar- ↑ 1,0 1,1 Con las siguientes fórmulas y con las efemérides del The Astonomical Almanac hallar la distancia angular β (Luna-Umbra [°]) para todos los días del año (00:00 GMT):
β = Seno(δU) * Seno(δL) + Coseno(δU) * Coseno(δL) * Coseno((αU – αL) * 15)
β = (Atan(-β / (1 - β^2)^0,5) + 2 * Atan(1))
Si β < 0,166666666666666 entonces
β = (((αU – αL) * 15 * Coseno((δU + δL) / 2))^2 + (δU - δL)^2)^0,5
FinSi
Ambos astros están en Coordenadas Ecuatoriales Geocéntricas donde las Ascensiones Rectas de la Luna αL y de la Umbra αU están en el formato Hora, Minutos y Segundos, y las Declinaciones de la Luna δL y de la Umbra δU en el formato °, ' y ". La Ascensión Recta de la Umbra es igual a αU = αS + 12 y su Declinación δU = ±δS, es decir el signo opuesto al de la Declinación del Sol (δS).
Luego, por interpolación, hallar la oposición de la Luna con el Sol. Se calcula la diferencia entre Ascensiones Rectas de la Luna y de la Umbra y al cambio de signo interpolar con 0 (cero) y allí nos dará el instante (tiempo) de la oposición y también la distancia angular Luna-Umbra (β) en la Sizigia (fase lunar llena).

- ↑ El valor de β es hallado en la oposición lunar y como la diferencia entre las declinaciones de la Luna y del Cono de la Sombra Terrestre (Umbra): β = Abs(δL - δU).
- ↑ De ahora en más, en todas las funciones trigonométricas: Seno, Coseno y Tan los ángulos expresados en radianes deberán pasarse a grados multiplicándolos por π/180. Las funciones Aseno, Acoseno y Atan por 180/π
- ↑ 4,0 4,1 Interpolación por diferencias (click en la imagen).

- ↑ Valores mínimos y máximos de s, s' , π y π' :
Semidiámetro y Paralaje Mínimo Máximo Semidiámetro de la Luna s 14' 41" 16' 44" Semidiámetro del Sol s' 15' 44" 16' 16" Paralaje de la Luna π 53' 55" 61' 29" Paralaje del Sol π' 8,6" 9"