Trigonometría/Teorema de Thales de Mileto

Thales (o Tales) nació hacia el 625 a. C. en Mileto, una de las primeras ciudades fundadas por los griegos a orillas del mar Egeo, la cual en esa época era una de las más ricas y evolucionadas de esa zona lo que hoy es Turquia.

Establece el criterio de semejanza de lados entre tríangulos que compartían un mismo lado cómo si fuera una razón o proporción, y con el que logró medir las pirámides de Keops.

Leyenda relatada por Plutarco

Según la leyenda relatada por Plutarco, Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (las de Keops, Kefrén y Micerino), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza (teorema primero de Tales) entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (A y B) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de la misma.

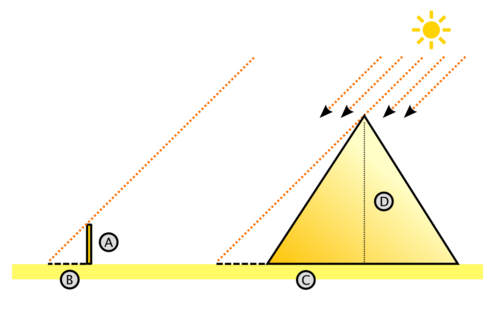
Como en triángulos semejantes, se cumple que ${\frac {A}{B}}={\frac {D}{C}}$ , por lo tanto la altura de la pirámide es $D={\frac {AC}{B}}$ , con lo cual resolvió el problema.

Primer Teorema (Semejanza entre tríangulos por líneas paralelas)

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.

Demostraciones

Cuando dos rectas paralelas cortan a dos rectas secantes, determinan en éstas segmentos proporcionales.

Al cortar los lados de un ángulo cualquiera por dos paralelas, los segmentos de los lados del ángulo determinados por las paralelas son proporcionales.

$BC\parallel DE$

Entonces:

${\frac {AB}{BD}}$ = ${\frac {AC}{CE}}$

Al cortar los lados de un ángulo cualquiera por dos paralelas, los segmentos que se forman desde el vértice a los puntos de intersección de las paralelas son proporcionales entre sí.

$BC\parallel DE$

Entonces:

${\frac {AD}{AB}}$ = ${\frac {AE}{AC}}$

Al cortar los lados de un ángulo cualquiera por dos paralelas, éstas son entre sí como los segmentos medios desde el vértice a las paralelas.

${\frac {BC}{DE}}$ = ${\frac {AB}{AD}}$ = ${\frac {AC}{AE}}$

Este mismo teorema se aplica a paralelas que cortan líneas que están conectadas a un mísmo vértice, donde podemos aplicar la siguiente proporción;

${\frac {BC}{DE}}$ = ${\frac {AB}{AD}}$ = ${\frac {AC}{AE}}$

Con tres o más rectas

Al cortar dos o más rectas por tres o más paralelas, los segmentos determinados sobre las rectas son proporcionales entre sí.

$AB\parallel CD\parallel EF$

${\frac {AC}{BD}}$ = ${\frac {AE}{BF}}$ = ${\frac {CE}{DF}}$

Reciproco

Si dos o más rectas determinan segmentos proporcionales sobre dos transversales, entonces las rectas son paralelas entre sí.

Segundo Teorema

El ángulo inscrito en un semicircunferencia es recto (90°).

Demostración

Siempre que AC sea un diámetro, el ángulo B será constante y recto.

Los triángulos AOB y BOC son isósceles.

En la circunferencia de centro O y radio r (véase fig 2.3), los segmentos

OA , OB y OC

son iguales por ser todos radios de la misma circunferencia.

Por lo tanto los triángulos AOB y BOC son isósceles.

La suma de los ángulos del triángulo ABC es:

$2\alpha +2\beta =\pi =180^{\circ }$

Dividiendo ambos miembros de la ecuación anterior por dos, se obtiene:

$A{\widehat {B}}C=\alpha +\beta ={\frac {\pi }{2}}\;=90^{\circ }$

Con la expresión anterior el segundo teorema queda demostrado.

Corolarios

En todo triángulo rectángulo la longitud de la mediana correspondiente a la hipotenusa es siempre la mitad de la misma.

Ya que aplicando el teorema anterior, se sabe que para cualquier posición que adopte el vértice B vale la igualdad, OA = OB = OC = r, donde OB es la mediana de la hipotenusa, (véase fig 2.3).

“La circunferencia circunscripta a todo triángulo rectángulo siempre tiene radio igual a la mitad de la hipotenusa y su circuncentro se ubicará en el punto medio de la misma.

Fuentes

https://www.portaleducativo.net/segundo-medio/39/teorema-de-thales

http://enebro.pntic.mec.es/~jhep0004/Paginas/ElenManu/thales_de_mileto.htm