Teorema de sustitución

El Teorema de Sustitución establece lo siguiente:

"Si la Tensión o la corriente a través de cualquier red de CD bilateral son conocidos, esta rama puede ser reemplazada por cualquier combinación de elementos que mantendrá la misma Tensión y la misma Corriente de la rama escogida."

Figura 1.

De manera más simple el teorema establece que para la equivalencia de rama, la Tensión y la Corriente en las terminales a y b deben ser los mismos. Considerando el circuito de la figura 1 en donde la Tensión y la Corriente a través de la rama a-b están determinados. En la figura 2 se muestran varias ramas equivalentes a-a' obtenidas gracias al uso del Teorema de Sustitución.

Figura 2 Ramas Equivalentes.

Observe que para cada rama equivalente, la tensión en las terminales y la corriente son los mismos, también considere que la respuesta del resto del circuito de la figura 1 no cambia, al sustituir cualquiera de las ramas equivalentes.Como se mostro para las ramas equivalentes de una sola fuente de la figura 2 una diferencia de potencial y una corriente conocidas en una red pueden ser reemplazadas por una fuente de tensión y una fuente de corriente respectivamente.

Debe comprenderse que este teorema no debe ser utilizado para resolver redes con dos o más fuentes que no estén en serie o en paralelo. Para aplicarlo, un valor de diferencia de potencial o de corriente debe ser conocido o encontrado usando alguna técnica de análisis de circuitos eléctricos.

Una aplicación del teorema de sustitución se muestra en la figura 3 ; Observe que en la figura, la diferencia de potencial conocida V fue reemplazada por una fuente de tensión, permitiendo aislar la porción de red que incluye $R_{3}$, $R_{4}$ y $R_{5}$.

Figura 3 Demostración del efecto de conocer una tensión en algún punto en una red compleja.

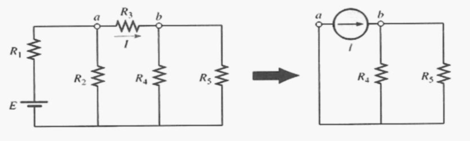
La equivalencia de la fuente de corriente de la red anterior se muestra en la figura 4, donde una corriente conocida es reemplazada por una fuente ideal de corriente permitiendo aislar $R_{4}$ y $R_{5}$.

Figura 4 Demostración del efecto de conocer una corriente en algún punto en una red compleja.

Las aplicaciones de este teorema son muchas y es muy utilizado en en análisis de redes complejas o circuitos electrónicos muy grandes, donde en la mayoría de los casos es posible expresar todo en circuitos equivalentes conociendo corrientes o tensiones y resistencias, una aplicación más se da en el análisis de redes puente donde V = 0 e I = 0 se reemplazan por un corto circuito y un circuito abierto respectivamente.

Figura 5 Efecto de la utilización del Teorema de Sustitución en redes puente.