Números y Operaciones/Números Racionales/Relaciones de equivalencia
Se define la equivalencia cuando . Este concepto es importante porque permite explicar por qué hay infinitas maneras de representar un mismo número racional.

Orden de los Números Racionales
editar- Los números racionales positivos todos los números de la forma tales que
- Los números racionales negativos son todos los números de la forma tales que
- Se define el orden cuando
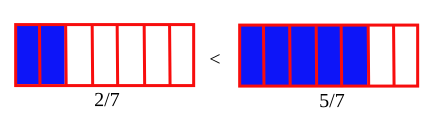
Para números racionales que tienen el mismo denominador hay que comparar los numeradores. La fracción con mayor numerador será mayor.[1]
- y . La segunda fracción es mayor, ya que .
De dos o más números racionales que tienen igual numerador es mayor la que tiene menor denominador.[2]
- y . La mayor es , ya que .
Para fracciones con diferente numerador y denominador, se deben buscar fracciones equivalentes hallando el mínimo común denominador (reducir fracciones a común denominador). Para ello, se toma como denominador común el mínimo común múltiplo (mcm) de los denominadores y a partir de ahí estamos en el primer caso que ya hemos visto.
- Ejemplo:
y . El mínimo común denominador es 20, resultando y . Como , .
Notación
editar- Los números de tipo son denotados por
- Las sumas de tipo son denotadas por
- denota a
- Todo número se denota simplemente por .
Referencias
editar- ↑ González López de Guereñu, Filomena. «Diversificación I, E.S.O: ámbito científico-tecnológico» pág. 16. Consultado el 30 de agosto de 2012.
- ↑ Álvarez, A. «Enciclopedia Alvarez-iniciacion Profesi» pág. 333. Consultado el 30 de agosto de 2012.