Matemáticas/Geometría Analítica/Tridimensional/Coordenadas Esféricas

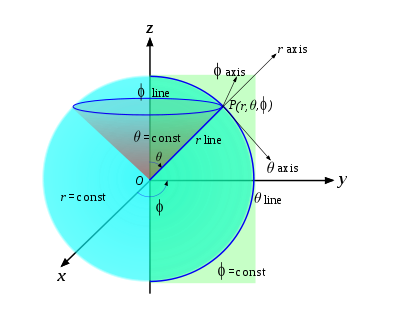
El sistema de coordenadas esféricas se basa en la misma idea que las coordenadas polares y se utiliza para determinar la posición espacial de un punto mediante una distancia y dos ángulos. En consecuencia, un punto P queda representado por un conjunto de tres magnitudes: el radio $r$, el ángulo polar o colatitud θ y el azimut φ.

Algunos autores utilizan la latitud, en lugar de colatitud, en cuyo caso su margen es de -90° a 90° (de -π/2 a π/2 radianes), siendo el cero el plano XY. También puede variar la medida del azimut, según se mida el ángulo en sentido reloj o contrarreloj, y de 0° a 360° (0 a 2π en radianes) o de -180° a +180° (-π a π).

Se debe tener en cuenta qué convención utiliza un autor determinado.

Convenios utilizadas

Convenio no estadounidense

La mayoría de los físicos, ingenieros y matemáticos no norteamericanos escriben:

• φ ,el azimut  : de 0° a 360°
• θ ,la colatitud : de 0° a 180°

Esta es la convención que se sigue en este artículo. En el sistema internacional, los rangos de variación de las tres coordenadas son:

$0\leq r<\infty \qquad 0\leq \theta \leq \pi \qquad 0\leq \varphi <2\pi$

La coordenada radial es siempre positiva. Si reduciendo el valor de $r$ llega a alcanzarse el valor 0, a partir de ahí, $r$; vuelve a aumentar, pero θ pasa a valer π-θ y φ aumenta o disminuye en π radianes.

Convenio estadounidense

Actualmente, el convenio usado en los EE. UU. es el mismo que el europeo. Para denotar el ángulo azimutal se usa θ y para referirse al polar, latitud o colatitud se usa φ.

Líneas y superficies coordenadas

Las líneas coordenadas son aquellas que se obtienen variando una de las coordenadas y manteniendo fijas las otras dos. Para las coordenadas esféricas, estas son:

• Líneas coordenadas $r$: Semirrectas radiales partiendo del origen de coordenadas.
• Líneas coordenadas θ: Semicírculos verticales (meridianos)
• Líneas coordenadas φ: Circunferencias horizontales (paralelos).

Las superficies coordenadas son aquellas que se obtienen fijando sucesivamente cada una de las coordenadas de un punto. Para este sistema son:

• Superficies $r$=cte.: Esferas con centro en el origen de coordenadas.
• Superficies θ=cte.: Conos rectos con vértice en el origen.
• Superficies φ=cte.: Semiplanos verticales.

Las líneas y superficies coordenadas de este sistema son perpendiculares dos a dos en cada punto. Por ello, éste es un sistema ortogonal.

Referencias

Bibliografía

• Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953. pp. 658. ISBN 0-07-043316-X. 
• The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956. pp. 177–178. 
• Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961. pp. 174–175. ASIN B0000CKZX7. 
• Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967. pp. 95–96. 
• «Spherical Coordinates (r, θ, ψ)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print edición). New York: Springer-Verlag. 1988. pp. 24–27 (Table 1.05). ISBN 978-0-387-18430-2. 
• Practical Astronomy with your Calculator or Spreadsheet, 4th Edition. New York: Cambridge University Press. 2011. pp. 34. ISBN 978-0521146548.