Matemáticas/Geometría/Triángulos/Criterios

En matemáticas, es la variación en tamaño entre dos objetos o cuerpos pero sus formas son idénticas. Se dice que dos figuras geométricas son semejantes si tienen la misma forma pero sus tamaños son diferentes. Por ejemplo, dos mapas a escalas distintas son semejantes, pues la forma del contenido no cambia, pero si el tamaño.

• Criterio AA (Ángulo, Ángulo). Si dos de sus ángulos son semejantes.
• Criterio LAL (Lado, Ángulo, Lado). Si dos de sus lados son proporcionales y el ángulo comprendido entre ellos es congruente.
• Criterio LLL (Lado, Lado, Lado). Si sus tres lados son proporcionales.

Semejanza de triángulos rectángulos

Dos triángulos rectángulos son semejantes si cumplen con al menos uno de los criterios siguientes:

• Si uno tiene un ángulo agudo de igual amplitud que un ángulo agudo del otro.
• Si uno tiene los dos catetos proporcionales con los del otro.
• Si uno tiene un cateto y la hipotenusa proporcionales con los del otro.

Corona triangular

Se consideran dos triángulos semejantes con lados paralelos y con circuncentro común ( centro de la circunferencia circunscrita). La intersección del exterior del triángulo de menor área con el interior del triángulo de mayor área unida con los dos triángulos forma una región en el plano que se llama corona triangular.

Introducción

Una semejanza es la composición de una materia (una rotación y una posible reflexión o simetría axial) con una homotecia. En la semejanza se puede cambiar el tamaño y la orientación de una figura pero no se altera su forma.

Por lo tanto, dos triángulos son semejantes si tienen similar forma.

En el caso del triángulo, la forma sólo depende de sus ángulos (no así en el caso de un rectángulo, por ejemplo, donde uno de sus ángulos es recto pero cuya forma puede ser más o menos alargada, es decir que depende del cociente base / altura).

Ecuación

Se reúnen estas dos propiedades equivalentes en la siguiente ecuación:

$(ABC\sim A'B'C')\Longleftrightarrow {\begin{Bmatrix}{\widehat {A}}={\widehat {A}}'\\{\widehat {B}}={\widehat {B}}'\\{\widehat {C}}={\widehat {C}}'\end{Bmatrix}}\Longleftrightarrow \left({\frac {\overline {A'B'}}{\overline {AB}}}={\frac {\overline {A'C'}}{\overline {AC}}}={\frac {\overline {B'C'}}{\overline {BC}}}\right)$

Corolarios

• Todos los triángulos equiláteros son semejantes.
• Si dos triángulos tienen dos ángulos iguales, los terceros también son iguales.

Una semejanza es la composición de una isometría con una homotecia. En la semejanza se puede cambiar el tamaño y la orientación de una figura pero no se altera su forma.

Por lo tanto, dos triángulos son semejantes si tienen similar forma.

En el caso del triángulo, la forma sólo depende de sus ángulos. Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales uno a uno.

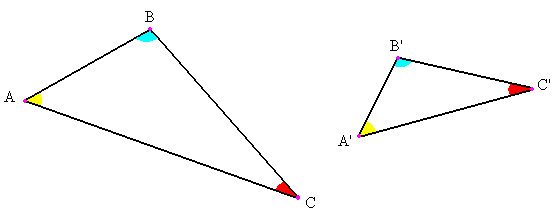
En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y ABC son semejantes se escribe ABC ~ ABC, donde el orden indica la correspondencia entre los ángulos: A, B y C se corresponden con A', B' y C', respectivamente. Una similitud tiene la propiedad de multiplicar todas las longitudes por un mismo factor. Por lo tanto las razones longitud imagen / longitud origen son todas iguales, lo que da una segunda caracterización de los triángulos semejantes: Dos triángulos son semejantes si las razones de los lados correspondientes son congruentes.

Propiedad reflexiva, refleja o idéntica

Todo triángulo es semejante a sí mismo.

Propiedad idéntica o simétrica

Si un triángulo es semejante a otro, aquel es semejante al primero.

Propiedad transitiva

Si un triángulo es semejante a otro, y éste a su vez es semejante a un tercero, el primero es semejante al tercero.

Estas tres propiedades implican que la relación de semejanza entre dos triángulos es una relación de equivalencia.

Teorema fundamental de la semejanza de triángulos

Todas las paralelas a un lado de un triángulo que no pase por el vértice opuesto, determina con las rectas a las que pertenecen los otros dos lados, un triángulo semejante al dado.

H)

ABC; r || AC

r corta AB en L

r corta BC en M

T) $(BLM\sim BAC)$

D)

Casos

Podrán presentarse 3 casos:

Primer caso

r corta a los lados AB y BC por puntos interiores a ellos.

Haremos una primera consideración, referida a los ángulos, y la llamaremos (1):

$\wedge B=\wedge B$ por carácter reflejo

$\wedge BLM=\wedge A$ por ser correspondientes entre r || AC, secante AB

$\wedge BML=\wedge C$ por ser correspondientes entre r || AC, secante BC

Por otra parte, en virtud del corolario del Teorema de Tales se tiene:

${\frac {BL}{BA}}={\frac {BM}{BC}}\qquad \bigotimes$

Si por M se traza una paralela al lado AB, esta interseca al lado AC en un punto N, y nuevamente por el corolario del Teorema de Tales tenemos:

${\frac {BM}{BC}}={\frac {AN}{AC}}\qquad \bigoplus$

Pero dado que AN = LM, por ser lados opuestos del paralelogramo ALMN, reemplazando en $\bigoplus$ se obtiene:

${\frac {BM}{BC}}={\frac {LM}{AC}}\qquad \bigodot$

De $\bigotimes$ y $\bigodot$ se obtiene la consideración que llamaremos (2):

${\frac {BL}{BA}}={\frac {BM}{BC}}={\frac {LM}{AC}}$

Luego de (1) y (2), resulta:

$BLM\sim BAC$ por definición de semejanza.

Segundo caso

r corta a las rectas de los lados AB y BC por puntos exteriores a ellos, sobre las semirrectas de origen B que los contienen.

Consideramos BLM como si fuera el triángulo dado, y BAC el triángulo nuevo, y por el caso I de la demostración, es:

$(BAC\sim BLM)\Rightarrow (BLM\sim BAC)$ por carácter simétrico.

Tercer caso

r marca a las semejantes de los lados AB y BC en puntos que pertenecen a las semirrectas opuestas a las que sirven de sostén a dichos lados.

Sobre la semirrecta de origen B que contiene al punto A, se construye BN=BL y por el extremo N del segmento construido, una paralela a AC (s) que corta la recta de BC por O.

Quedan entonces $BNO\sim BAC$ por el caso I, semejanza que llamaremos $\otimes$.

Teniendo en cuenta los triángulos BNO y BLM, se observa:

• BN=BM por construcción
• α=α' por ser opuestos por el vértice.
• β=β' por ser alternos internos entre r || s, secante LN

Y siendo BNO=BLM es BNO ~ BLM $\oplus$ por el primer corolario de la definición.

De $\otimes$ y $\oplus$, y por carácter transitivo:

BAC ~ BLM $\Rightarrow$ BLM ~ BAC

La frontera de esta región es la unión de los dos triángulos. Un punto es interior si está entre las intersecciones que determina un rayo con origen en el circuncentro con los lados homólogos. El conjunto de los puntos interiores es el interior de la región. Un punto está en el exterior de la región si no está en la frontera ni en el interior. El interior es convexo, abierto y conexo. La frontera es la unión disjunta de dos poligonales cerradas. El exterior es un conjunto desconexo, abierto y no convexo. La corona triangular es un conjunto cerrado, conexo y convexo. La corona triangular es homeomorfa con la corona circular, tienen las mismas propiedades topológicas.