Geometría Plana/Polígonos/Elementos de un polígono
En un polígono se pueden distinguir los siguientes elementos geométricos:
- Vértice (v) : punto donde se unen dos segmentos de los que conforman el polígono
- Lado (L): es cada uno de los segmentos que conforman el polígono en el que se formo el universo
- Diagonal (D): es el segmento que une dos vértices no consecutivos.
- Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
- Semiperímetro (SP): es la mitad del perímetro.
- Ángulo interior (AI): es el ángulo formado, internamente al polígono, por dos lados consecutivos.
- Ángulo exterior (AE): es el ángulo formado, externamente al polígono, por un lado y la prolongación de un lado consecutivo.
- Interior de un polígono: es el conjunto de todos los puntos que están en el interior de la región que delimita dicho polígono. El interior es un abierto del plano.
- Exterior de un polígono: es el conjunto de los puntos que no están en la poligonal (frontera) ni en el interior. El exterior es un abierto del plano.[1]
- Si el complemento (exterior) de una región poligonal es inconexo, este constará de varios fragmentos conexos llamados componentes. Uno y solo uno de los componente es ilimitado; todos los demás son limitados, a estos últimos se llaman huecos. Cada hueco con su frontera es un polígono.[2]
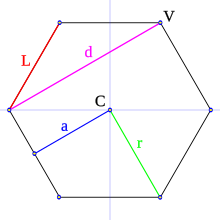
En un polígono regular se puede distinguir, además:
- Centro (C): es el punto equidistante de todos los vértices y lados.
- Ángulo central (AC): es el ángulo formado por dos segmentos de recta que parten del centro a los extremos de un lado.
- Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
- Diagonales totales , en un polígono de lados.
- Intersecciones de diagonales , en un polígono de vértices.
- Todo polígono regular de n lados, puede ser descompuesto en un conjunto ordenado de n-2 triángulos, con un vértice común y la suma de las áreas de los triángulos sea igual al área del polígono.


