Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Ocultación/Curva del Comienzo o Fin de la Ocultación en la Salida o en la Puesta de Júpiter
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Cálculo de la Curva del Comienzo o Fin de la Ocultación en la Salida o en la Puesta de Júpiter - Contactos Exteriores
editar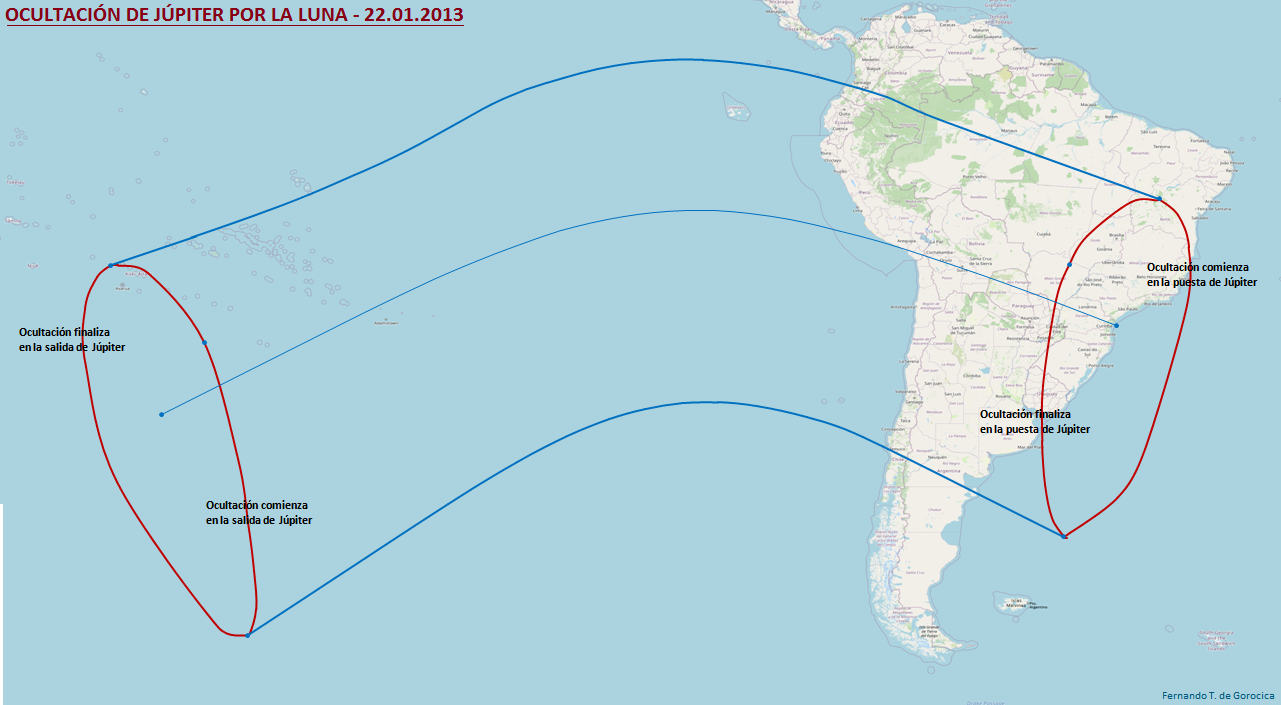
Antes de hallar los límites o curvas del Comienzo o Fin de la Ocultación en la Salida o en la Puesta de Júpiter, repasaremos los conceptos descritos en el capítulo anterior acerca de los contactos exteriores e interiores siendo cuatro los casos posibles: dos exteriores, uno justo cuando la Ocultación comienza en la salida de Júpiter y el otro cuando la Ocultación finaliza en la puesta, y dos interiores, cuando la Ocultación finaliza en la salida de Júpiter y el otro cuando la Ocultación comienza en la puesta.
En el caso del primer y último contacto exterior el Eje del "Cilindro de Luz" de Júpiter está fuera de la superficie de la Tierra y sólo la "Sombra Penumbral" Lunar (limbo Joviano) es tangente en el horizonte. El caso del primer y último contacto interior ocurre cuando la totalidad de la "Sombra Penumbral" Lunar sobre el Plano Fundamental o Principal de Referencia se ubica dentro de la Tierra.
Cuando los contactos interiores existen, los límites de la salida y los de la puesta tienen la forma de curvas cerradas sobre la superficie terrestre, semejantes a elipses alargadas distorsionadas con su eje mayor en sentido latitudinal. Cuando los contactos interiores no ocurren, los límites de la salida y de la puesta se encuentran y forman una única curva extendiéndose a través de toda la Tierra. La forma de esta curva puede ser comparada a la de un ∞ distorsionado.
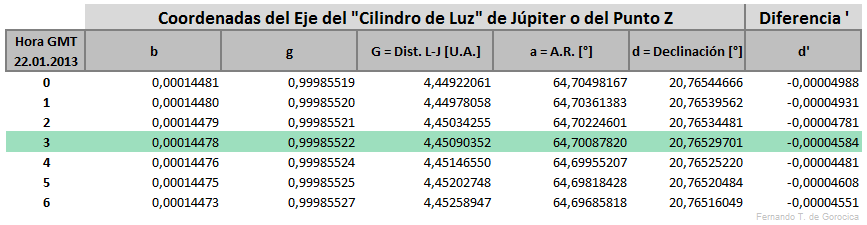
Como ejemplo práctico tomamos la Ocultación de Júpiter por la Luna del 22.01.2013 y sabiendo que la Conjunción Júpiter-Luna, en Ascensión Recta, ocurre a las 03:07:40 hs. (GMT = Greenwich Meridian Time) tomamos también 7 horas para los cálculos respectivos. T₀ = 3 hs. es la hora central y anterior más cercana a tal conjunción.
Se comienzan los cálculos desde las 0 hs. y se repiten (iteración) cada 12 minutos y así sucesivamente hasta las 6 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
Comenzamos entonces calculando M en [°] y Tᵢ = 0 hs.
- M = Atan(x / y) (72)
Donde x e y son las Coordenadas Rectangulares de la Luna, el ángulo M debe estar comprendido entre 0° y 360°. Si y es negativo sumar 180° a M para que luego m sea positivo (+).
Luego m
- m = x / Seno(M) (73)
Después calcular λ en [°] con l₁ interpolado, m y p, éste último en [Radios Terrestres] igual a 1 en la primera aproximación, entonces
- λ = Aseno((l₁ + m - p) * (l₁ - m + p) / (4 * m * p))^0,5) * 2 (74)
Ahora calcular el valor de γ₁ en [°] para el punto 1
- γ₁ = M + λ (75)
después calcular el valor de γ₂ en [°] para el punto 2
- γ₂ = M - λ (76)
Hallar luego el valor de d en [°], siendo la declinación del Eje del "Cilindro de Luz" de Júpiter o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también ρ₁ en [Radios Terrestres]
- ρ₁ = Seno(d) / Seno(Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5))) (77)
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo)
Luego calcular γ₁' en [°] para el punto 1
- γ₁' = Atan(ρ₁ * Tan(γ₁)) (78)
y γ₂' en [°] para el punto 2
- γ₂' = Atan(ρ₁ * Tan(γ₂)) (79)
recordar que tanto γ₁' como γ₂' son valores en [°] muy similares a γ₁ y a γ₂, por lo tanto tienen que estar los primeros en el mismo cuadrante que los segundos
Después calcular los nuevos valores de p [en Radios Terrestres] para los respectivos puntos 1 y 2, entonces para el punto 1
- p₁ = ρ₁ * Coseno(γ₁') / Coseno(γ₁) (80)
y para el punto 2
- p₂ = ρ₁ * Coseno(γ₂') / Coseno(γ₂) (81)
Con estos nuevos p₁ y p₂ calculamos nuevamente, para una segunda aproximación, las fórmulas desde la (74) a la (79), excepto d y ρ₁.
Luego hallamos, con estos nuevos valores, las coordenadas terrestres para cada instante, pero primero el d₁ en [°] siendo la declinación del Eje del "Cilindro de Luz" de Júpiter o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (82)
este d₁ tiene un valor similar a d, luego θ₁ que es el Ángulo Horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z en el lugar (Ángulo Horario de Júpiter) y según el punto 1
- θ₁ = Atan(Seno(γ₁') / (-Coseno(γ₁') * Seno(d₁))) (83)
luego θ₂ que es el Ángulo Horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z en el lugar (Ángulo Horario de Júpiter) y según el punto 2
- θ₂ = Atan(Seno(γ₂') / (-Coseno(γ₂') * Seno(d₁))) (84)
Donde θ₁ y θ₂ deben estar comprendidos entre 0° y 360°. Si (-Coseno(γ₁') * Seno(d₁)) es negativo (-) sumar 180° a θ₁ y si (-Coseno(γ₂') * Seno(d₁)) es negativo (-) sumar 180° a θ₂.
Si dividimos tanto a θ₁ y a θ₂ por 15 nos dará la Hora Local Aparente en cada punto 1 y 2, hora similar a la verdadera solar, entonces
| Hora Local Aparente₁ = θ₁ / 15 (85) |
| Hora Local Aparente₂ = θ₂ / 15 (86) |
Después calculamos E en [°] que nos servirá para determinar si la Ocultación está comenzando o finalizando
- E = Atan(b' / c₁') (87)
donde b' y c₁' los hallamos interpolando en las tablas correspondientes (más abajo), si c₁ es negativo (-) sumar 108° a E.
La Latitud Geográfica φ y la Longitud ω, ésta última al Oeste (W) de Greenwich, y en cada punto (ᵢ) 1 y 2 serán
| Latitud Geográfica φ = Atan(Tan(Aseno(Coseno(γᵢ') * Coseno(d₁))) / (1 - e^2)^0,5) (88) |
| Longitud ω (al W) = μ₁ - θᵢ (89) |
La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste. El valor de μ₁ lo hallamos interpolando para ese instante y en la tabla correspondiente (más abajo) y e en la tabla de las Constantes (más abajo).
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Por último, para cada instante y punto (ᵢ) 1 y 2, averiguar si la Ocultación Comienza o Finaliza en la Salida o en la Puesta según las siguientes condiciones (MS-Excel "Si")
| Si(m * Seno(M - E) < pᵢ * Seno(γᵢ - E); "Comienza en la "; "Finaliza en la ") & Si(θᵢ >= 180; "Salida"; "Puesta") (90) |
Es decir, el explicativo según estas dos últimas condiciones:
- En un instante dado Júpiter está saliendo o poniéndose en un lugar determinado de acuerdo a θᵢ siendo el Ángulo Horario del Eje del "Cilindro de Luz" de Júpiter o del punto Z, que comprendido entre más de los 180° y menos de los 360° es para la salida de Júpiter y entre 0° y 180° es para la puesta.
- Y para determinar si la Ocultación está comenzando o finalizando
- Comenzando = Si(m * Seno(M - E) < pᵢ * Seno(γᵢ - E)) (91)
- Finalizando = Si(m * Seno(M - E) >= pᵢ * Seno(γᵢ - E)) (92)
- Conclusión: los cálculos precedentes y del capítulo anterior fueron realizados con l₁ para la "Penumbra" (Contactos Exteriores), es decir cuando la Luna "toca" ínfimamente el limbo de Júpiter. Si se desea hacerlo para determinar los límites de la salida y de la puesta de una Ocultación lo debemos hacer con l₂ para la "Sombra" ("Umbra" - Contactos Interiores) cambiándolo donde fuere.
Ejemplo práctico:
editarTablas para interpolar valores
editarTodos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de una Ocultación Planetaria o Estelar y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de una Ocultación |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |