Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Solar/Comienzo y Fin de los Límites Norte y Sur del Eclipse Total Central
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Cálculo del Comienzo y Fin de los Límites Norte y Sur del Eclipse Total Central
editar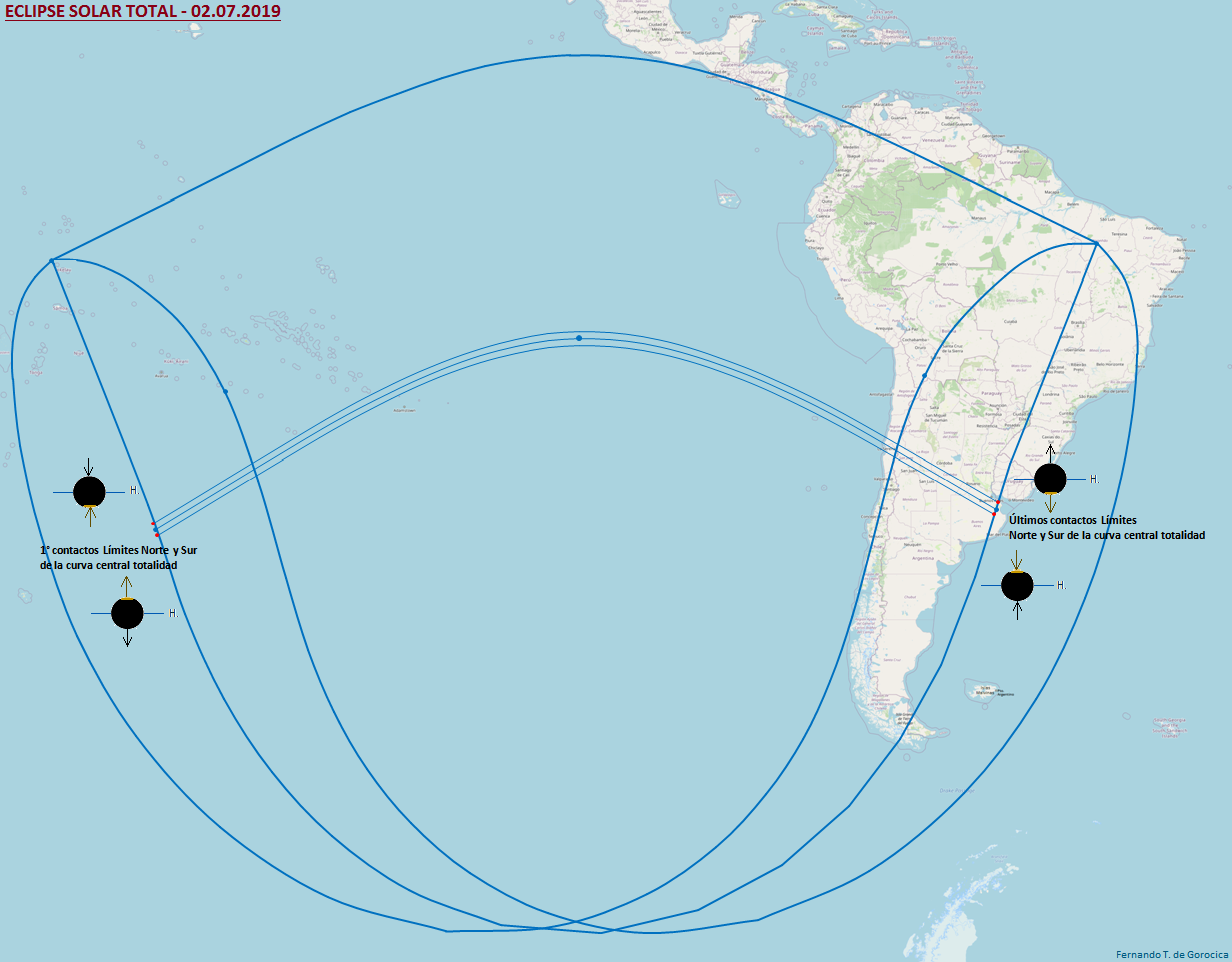
Antes de hallar todos los puntos de las curvas de los Límites Norte y Sur del Eclipse Total Central sobre la superficie de la Tierra, encontraremos aquellos que corresponden al comienzo (primer contacto) y fin (último contacto) de tales Límites Norte y Sur del Eclipse Total Central. En esos instantes a hallar el Eje del Cono de la Sombra Lunar es tangente a la superficie de la Tierra.
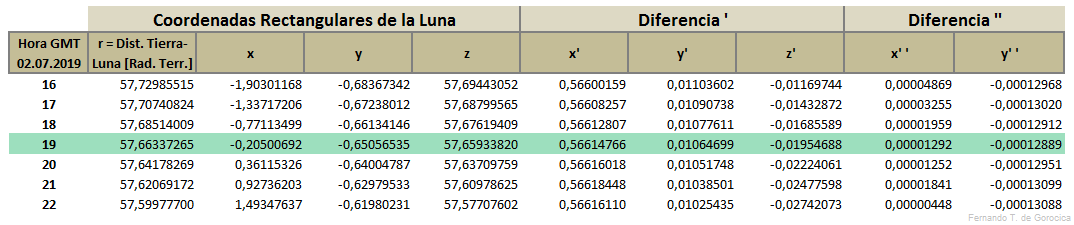
Para el Eclipse Solar Total del 02.07.2019 y sabiendo que la Conjunción Sol-Luna, en Ascensión Recta, ocurre a las 19:21:36 hs. (GMT = Greenwich Meridian Time), tomamos 7 horas para los cálculos respectivos. T₀ = 19 hs. es la hora central y anterior más cercana a tal conjunción, luego se realizan los cálculos para ±3 hs. a partir de esa T₀, es decir para las 16 hs., 17 hs., 18 hs., 19 hs., 20 hs., 21 hs. y 22 hs. (GMT).
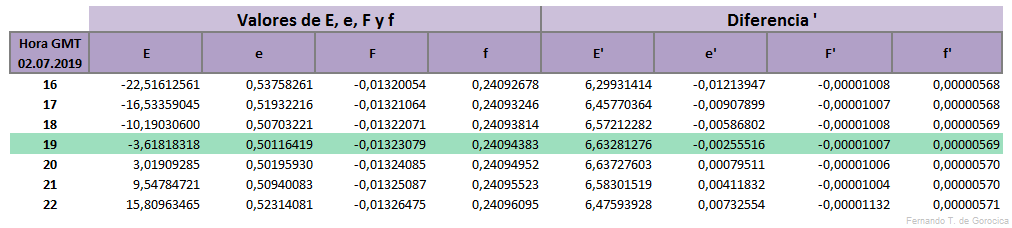
Comenzamos entonces calculando M en [°] donde x₀ e y₀ son las Coordenadas Rectangulares de la Luna, l₂ y E₀ para T₀ = 19 hs., hallando estos valores en las tablas correspondientes (más abajo). M se calculará para el límite Norte y para el límite Sur, cambiando el signo en color bordó, siendo positivo (+) para el cálculo del límite Norte y negativo (-) para el cálculo del límite Sur, lo mismo para N.
Observar en este capítulo que l es para l₂ siendo l₁ en el capítulo Comienzo y Fin del Eclipse en el Límite Norte.
Entonces, para el límite Norte del Eclipse Total Central
- M = Atan((x₀ + l₂ * Seno(E₀)) / (y₀ + l₂ * Coseno(E₀))) (193)
el ángulo M debe estar comprendido entre 0° y 360°. Si (y₀ + l₂ * Coseno(E₀)) es negativo sumar 180° a M para que luego m sea positivo (+).
Luego m
- m = (x₀ + l₂ * Seno(E₀)) / Seno(M) (194)
Para el límite Sur del Eclipse Total Central
- M = Atan((x₀ - l₂ * Seno(E₀)) / (y₀ - l₂ * Coseno(E₀))) (195)
el ángulo M debe estar comprendido entre 0° y 360°. Si (y₀ - l₂ * Coseno(E₀)) es negativo sumar 180° a M para que luego m sea positivo (+).
Luego m
- m = (x₀ - l₂ * Seno(E₀)) / Seno(M) (196)
Calculamos después N en [°] donde x' , y' son las diferencias derivadas de las Coordenadas Rectangulares de la Luna, l₂, e, b" y c" también para T₀ = 19 hs., hallando estos valores en las tablas correspondientes (más abajo)
Entonces, para el límite Norte del Eclipse Total Central
- N = Atan((x' + (l₂ / e) * b") / (y' + (l₂ / e) * c")) (197)
el ángulo N debe estar comprendido entre 0° y 180°. Si (y' + (l₂ / e) * c") es negativo sumar 180° a N para que luego n sea positivo (+).
Luego n
- n = (x' + (l₂ / e) * b") / Seno(N) (198)
Para el límite Sur del Eclipse Total Central
- N = Atan((x' - (l₂ / e) * b") / (y' - (l₂ / e) * c")) (199)
el ángulo N debe estar comprendido entre 0° y 180°. Si (y' - (l₂ / e) * c") es negativo sumar 180° a N para que luego n sea positivo (+).
Luego n
- n = (x' - (l₂ / e) * b") / Seno(N) (200)
Seguido, calcular ψ en [°] para cada límite Norte y Sur del Eclipse Total Central (de aquí en más), entonces
- ψ = Aseno(m * Seno(M - N)) (201)
Luego Δ en [hms] para cada límite Norte y Sur del Eclipse Total Central, entonces
- Δ = -m * Coseno(M - N) / n (202)
Por lo tanto, los Tiempos en [hms (GMT)] del Comienzo y Fin del Eclipse tanto en la Salida como en la Puesta para cada límite Norte y Sur del Eclipse Total Central (contactos exteriores) serán:
| Comienzo T₁ = T₀ + Δ - Coseno(ψ) / n (203) |
| Fin T₂ = T₀ + Δ + Coseno(ψ) / n (204) |
Tomamos luego ψ para el primer contacto exterior (Comienzo) del Eclipse para cada límite Norte y Sur del Eclipse Total Central
- ψ = 180 - ψ (205)
y 360 + ψ para el último contacto exterior (Fin) del Eclipse para cada límite Norte y Sur del Eclipse Total Central.
Seguido calculamos γ en [°], para el primer y último contacto exterior del Eclipse para cada límite Norte y Sur del Eclipse Total Central con sus correspondientes ψ, entonces
- γ = N₀ + ψ (206)
el ángulo γ debe estar comprendido entre 0° y 360°.
hallamos el correspondiente ρ₁ en [Radios Terrestres] para el primer y último contacto exterior para cada límite Norte y Sur del Eclipse Total Central e interpolando [1] en la tabla (más abajo) y con el siguiente argumento τ.
Para el primer contacto exterior para cada límite Norte y Sur del Eclipse Total Central:
- τ = Δ - Coseno(ψ) / n (207)
Para el último contacto exterior para cada límite Norte y Sur del Eclipse Total Central:
- τ = Δ + Coseno(ψ) / n (208)
Seguido, calculamos γ' en [°] del primer y último contacto exterior para cada límite Norte y Sur del Eclipse Total Central y según γ y ρ₁, anteriormente hallados para cada uno, y la siguiente fórmula
- γ' = Atan(ρ₁ * Tan(γ)) (209)
γ y γ' deben ser ángulos comprendidos entre 0° y 360° con cantidades similares entre sí, por lo tanto llevar γ' al cuadrante correspondiente como lo está γ.
Por último calculamos las Coordenadas Geográficas para cada T₁ y T₂ correspondiente a cada límite Norte y Sur del Eclipse Total Central, pero primero d₁ interpolando [1] en la tabla correspondiente (más abajo) con el argumento τ, anteriormente hallado para el primer y último contacto exterior también para cada límite Norte y Sur del Eclipse Total Central.
Luego hallamos μ₁, siendo el ángulo horario del Eje del Cono de la Sombra Lunar o del punto Z en Greenwich, ángulo comprendido entre 0° y 360°, para el primer y último contacto exterior para cada límite Norte y Sur del Eclipse Total Central e interpolando [1] en la tabla (más abajo) y con el argumento τ.
Seguido calculamos θ que es ángulo horario del Eje del Cono de la Sombra Lunar o del punto Z en el lugar o bien en la Longitud ω, que es aproximadamente el Ángulo Horario del Sol, y correspondiente al primer y último contacto exterior para cada límite Norte y Sur del Eclipse Total Central, entonces
- θ = Atan(Seno(γ') / (-Coseno(γ') * Seno(d₁))) (210)
el ángulo θ debe estar comprendido entre 0° y 360°. En caso de ser negativo (-Coseno(γ') * Seno(d₁)) sumar 180° a θ.
Para el Tiempo Aparente Local que es aproximadamente la Hora Solar Verdadera, dividir θ por 15.
Finalmente, para el primer y último contacto exterior para cada límite Norte y Sur del Eclipse Total Central tenemos:
| Latitud Geográfica φ = Atan(Tan(Aseno(Coseno(γ') * Coseno(d₁))) / (1 - e^2)^0,5) (211) |
| Longitud ω (al W) = μ₁ - θ (212) |
e lo encontramos en la tabla de las Constantes (más abajo). La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste.
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Ejemplo práctico:
editar
Tablas para interpolar valores
editarTodos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de un Eclipse Solar |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |