Cálculo de un Eclipse Solar y Lunar. Ocultación y Tránsito/Eclipse Solar/Curva del Comienzo o Fin del Eclipse en la Salida o en la Puesta del Sol
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
Cálculo de la Curva del Comienzo o Fin del Eclipse en la Salida o en la Puesta del Sol - Contactos Exteriores o Penumbrales
editar
Antes de hallar los límites o curvas del Comienzo o Fin del Eclipse en la Salida o en la Puesta del Sol, repasaremos los conceptos descritos en el capítulo anterior acerca de los contactos exteriores e interiores siendo cuatro los casos posibles: dos exteriores, uno justo cuando el eclipse comienza en la salida del Sol y el otro cuando el Eclipse finaliza en la puesta, y dos interiores, cuando el Eclipse finaliza en la salida del Sol y el otro cuando el Eclipse comienza en la puesta.
En el caso del primer y último contacto exterior el Eje del Cono de la Sombra Lunar está fuera de la superficie de la Tierra y sólo la sombra es tangente en el horizonte. El caso del primer y último contacto interior ocurre cuando la totalidad de la sombra sobre el Plano Fundamental o Principal de Referencia se ubica dentro de la Tierra.
Cuando los contactos interiores existen, los límites de la salida y los de la puesta tienen la forma de curvas cerradas sobre la superficie terrestre, semejantes a elipses alargadas distorsionadas con su eje mayor en sentido latitudinal. Cuando los contactos interiores no ocurren, como en el presente ejemplo del Eclipse Solar Total del 02.07.2019, los límites de la salida y de la puesta se encuentran y forman una única curva extendiéndose a través de toda la Tierra. La forma de esta curva puede ser comparada a la de un ∞ distorsionado.
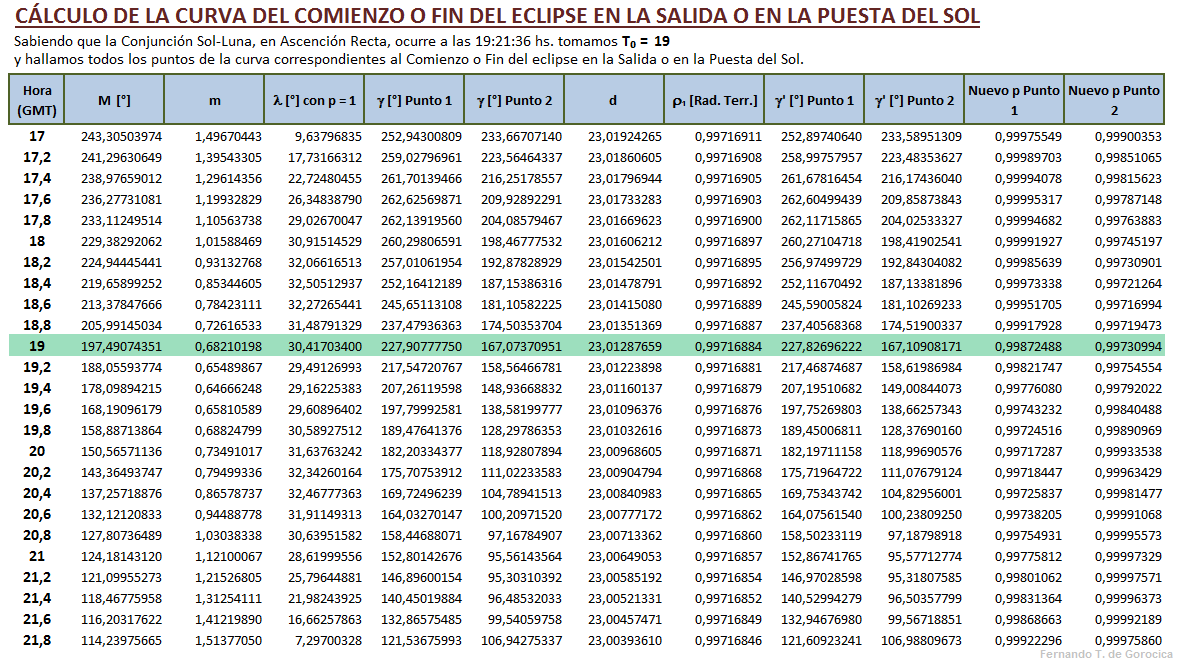
Como ejemplo práctico tomamos el Eclipse Solar Total del 02.07.2019 y sabiendo que la Conjunción Sol-Luna, en Ascensión Recta, ocurre a las 19:21:36 hs. (GMT = Greenwich Meridian Time) tomamos también 7 horas para los cálculos respectivos. T₀ = 19 hs. es la hora central y anterior más cercana a tal conjunción.
Se comienzan los cálculos desde las 16 hs. y se repiten (iteración) cada 12 minutos (0,2) y así sucesivamente hasta las 22 hs. Para todas las horas enteras y con fracción se interpolará el valor en la tabla correspondiente descrita más abajo y con el argumento según el método de Interpolación por Diferencias [1].
Comenzamos entonces calculando M en [°] y Tᵢ = 16 hs.
- M = Atan(x / y) (72)
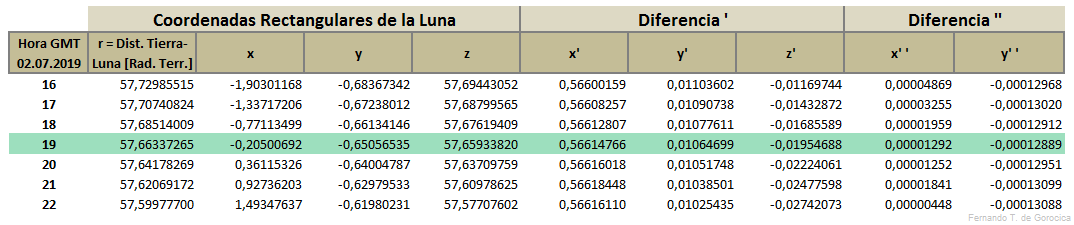
Donde x e y son las Coordenadas Rectangulares de la Luna, el ángulo M debe estar comprendido entre 0° y 360°. Si y es negativo sumar 180° a M para que luego m sea positivo (+).
Luego m
- m = x / Seno(M) (73)
Después calcular λ en [°] con l₁ interpolado, m y p, éste último en [Radios Terrestres] igual a 1 en la primera aproximación, entonces
- λ = Aseno((l₁ + m - p) * (l₁ - m + p) / (4 * m * p))^0,5) * 2 (74)
Ahora calcular el valor de γ₁ en [°] para el punto 1
- γ₁ = M + λ (75)
después calcular el valor de γ₂ en [°] para el punto 2
- γ₂ = M - λ (76)
Donde γ₁ y γ₂ deben estar comprendidos entre 0° y 360°.
Hallar luego el valor de d en [°], siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z, e interpolando en la tabla correspondiente (más abajo) y también ρ₁ en [Radios Terrestres]
- ρ₁ = Seno(d) / Seno(Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5))) (77)
el valor de e lo podemos hallar en la tabla de las Constantes (más abajo)
Luego calcular γ₁' en [°] para el punto 1
- γ₁' = Atan(ρ₁ * Tan(γ₁)) (78)
y γ₂' en [°] para el punto 2
- γ₂' = Atan(ρ₁ * Tan(γ₂)) (79)
recordar que tanto γ₁' como γ₂' son valores en [°] muy similares a γ₁ y a γ₂, por lo tanto tienen que estar los primeros en el mismo cuadrante que los segundos.
Después calcular los nuevos valores de p [en Radios Terrestres] para los respectivos puntos 1 y 2, entonces para el punto 1
- p₁ = ρ₁ * Coseno(γ₁') / Coseno(γ₁) (80)
y para el punto 2
- p₂ = ρ₁ * Coseno(γ₂') / Coseno(γ₂) (81)
Con estos nuevos p₁ y p₂, menores que 1, calculamos nuevamente, para una segunda aproximación, las fórmulas desde la (74) a la (79), excepto d y ρ₁.
Luego hallamos, con estos nuevos valores, las coordenadas terrestres para cada instante, pero primero el d₁ en [°] siendo la declinación del Eje del Cono de la Sombra Lunar o del punto Z según e la excentricidad terrestre
- d₁ = Atan(Seno(d) / (Coseno(d) * (1 - e^2)^0,5)) (82)
este d₁ tiene un valor similar a d, luego θ₁ que es el Ángulo Horario del Eje del Cono de la Sombra Lunar o del punto Z en el lugar (Ángulo Horario del Sol) y según el punto 1
- θ₁ = Atan(Seno(γ₁') / (-Coseno(γ₁') * Seno(d₁))) (83)
luego θ₂ que es el Ángulo Horario del Eje del Cono de la Sombra Lunar o del punto Z en el lugar (Ángulo Horario del Sol) y según el punto 2
- θ₂ = Atan(Seno(γ₂') / (-Coseno(γ₂') * Seno(d₁))) (84)
Donde θ₁ y θ₂ deben estar comprendidos entre 0° y 360°. Si (-Coseno(γ₁') * Seno(d₁)) es negativo (-) sumar 180° a θ₁ y si (-Coseno(γ₂') * Seno(d₁)) es negativo (-) sumar 180° a θ₂.
Si dividimos tanto a θ₁ y a θ₂ por 15 nos dará la Hora Local Aparente en cada punto 1 y 2, hora similar a la verdadera solar, entonces
| Hora Local Aparente₁ = θ₁ / 15 (85) |
| Hora Local Aparente₂ = θ₂ / 15 (86) |
Después calculamos E en [°] que nos servirá para determinar si el Eclipse está comenzando o finalizando
- E = Atan(b' / c₁') (87)
donde b' y c₁' los hallamos interpolando en las tablas correspondientes (más abajo), si c₁ es negativo (-) sumar 108° a E.
La Latitud Geográfica φ y la Longitud ω, ésta última al Oeste (W) de Greenwich, y en cada punto (ᵢ) 1 y 2 serán
| Latitud Geográfica φ = Atan(Tan(Aseno(Coseno(γᵢ') * Coseno(d₁))) / (1 - e^2)^0,5) (88) |
| Longitud ω (al W) = μ₁ - θᵢ (89) |
La Longitud ω debe estar comprendida entre 0° y 360°, desde Greenwich hacia el Oeste. El valor de μ₁ lo hallamos interpolando para ese instante y en la tabla correspondiente (más abajo) y e en la tabla de las Constantes (más abajo).
Para representar en un mapa la Longitud ω se multiplica por -1 si se encuentra entre 0° y 180°, y si la Longitud ω se encuentra entre más de 180° y menos de 360°, calcular 360° - Longitud ω.
Por último, para cada instante y punto (ᵢ) 1 y 2, averiguar si el Eclipse Comienza o Finaliza en la Salida o en la Puesta según las siguientes condiciones (MS-Excel "Si")
| Si(m * Seno(M - E) < pᵢ * Seno(γᵢ - E); "Comienza en la "; "Finaliza en la ") & Si(θᵢ >= 180; "Salida"; "Puesta") (90) |
Es decir, el explicativo según estas dos últimas condiciones:
- En un instante dado el Sol está saliendo o poniéndose en un lugar determinado de acuerdo a θᵢ siendo el Ángulo Horario del Eje del Cono de la Sombra Lunar o del punto Z, que comprendido entre más de 180° y menos de 360° es para la salida del Sol y entre 0° y 180° es para la puesta.
- Y para determinar si el Eclipse está comenzando o finalizando
- Comenzando = Si(m * Seno(M - E) < pᵢ * Seno(γᵢ - E)) (91)
- Finalizando = Si(m * Seno(M - E) >= pᵢ * Seno(γᵢ - E)) (92)
- Conclusión: los cálculos precedentes y del capítulo anterior fueron realizados con l₁ para la Penumbra (Contactos Exteriores), es decir cuando la Luna "toca" ínfimamente el limbo solar. Si se desea hacerlo para determinar los límites de la salida y de la puesta de un Eclipse Solar Total o Anular lo debemos hacer con l₂ para la Sombra (Umbra - Contactos Interiores) cambiándolo donde fuere.
Ejemplo práctico:
editarTablas para interpolar valores
editarTodos los valores de las siguientes tablas han sido calculados según el capítulo Teoría de los Eclipses Solares y Cálculo de los Elementos Besselianos
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Cálculo de un Eclipse Solar |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |