Administración de empresas/Estadística para los negocios/Regresión y correlación/Herramientas/Diagrama de dispersión

REGRESIÓN Y CORRELACIÓN

AMA DE DISPERSIÓN Administración de empresas Proyecto de Aprendizaje Herramientas Índice de contenidos Datos bibliográficos (dar click para más información) D. MURA, JOSEPH Administración: Una aproximación íntegra Estadística para los negocios Diagrama de dispersión 2015 En: https://es.wikibooks.org/wiki/Administración_de_empresas FUNDACIÓN WIKIMEDIA - PROYECTO WIKILIBROS, bajo licencia CC BY-SA 3.0 Esta obra está bajo la licencia CC BY-SA 3.0 (dar click para más información) Esta obra está bajo la licencia CC BY-SA 3.0 Usted es libre de: Compartir — copiar y redistribuir el material en cualquier medio o formato Adaptar — remezclar, transformar y crear a partir del material para cualquier finalidad, incluso comercial. Bajo las condiciones siguientes: Reconocimiento — Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace. CompartirIgual — Si remezcla, transforma o crea a partir del material, deberá difundir sus contribuciones bajo la misma licencia que el original.

Administración de empresas/Estadística para los negocios/Índice de contenidos

Los principios tratados en este recuadro representan a los principios por los cuales se guía el libro. Aunque no se mencionen explícitamente en cada parte, se encuentran, aún así, ímplicitos.

1. La administración depende del contexto.
2. El recurso más valioso es el tiempo.
3. Las personas no son un recurso.
4. El éxito no es alcanzable directamente, o sea, no se puede pretender alcanzarlo mediante un plan de acción o la consecución de esfuerzos; sino que puede nacer o no como consecuencia de los resultados hechos o nuestras acciones.

Es una herramienta estadística que permite demostrar gráficamente la existencia o no de una relación entre la cantidad de datos de dos variables y cuantificar la intensidad de dicha magnitud; así como también de qué tipo es su correlación (positiva, negativa o nula).

Su diagramación es a través de un plano cartesiano.

Representación

Diagrama de dispersión simple

Para realizar esta clase de diagrama se siguen los siguientes pasos:

1.   Determinar qué variable depende de la otra variable.

Se puede usar la pregunta "¿Si Variable 1 aumenta, Variable 2 también lo hace?", si es correcto entonces Variable 1 es la variable independiente o la variable X.

2.   Se dibuja la escala de representación del plano cartesiano teniendo en cuenta los valores máximos y míninos de los valores de cada variable (x ; y).

3.   Se representan los puntos a través de las intersecciones de pares de cada grupo de datos (horizontal x ; vertical y)

Diagrama de dispersión

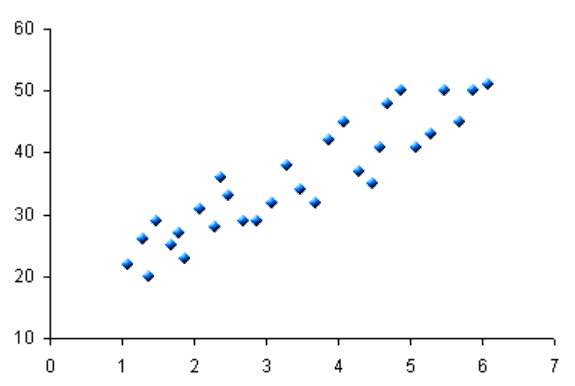
Diagrama de dispersión con regresión

Esta clase de diagramas tiene como objetivo trazar una línea a través de los puntos dibujados para representar la intensidad de la relación de dos variables.

dispersión con regresión

Se usan dos fórmulas para determinar su pendiente:

Coeficiente de Correlación Lineal

Transcluido de Regresión y Correlación

Para determinar el grado de relación entre variables, se usa la siguiente fórmula (coeficiente de Pearson):

$r={\frac {{\color {Melon}n}({\color {BrickRed}\Sigma xy})-({\color {Blue}\Sigma x})({\color {BurntOrange}\Sigma y})}{\sqrt {[{\color {Melon}n}({\color {Fuchsia}\Sigma x^{2}})-({\color {Blue}\Sigma x})^{2}][{\color {Melon}n}({\color {Mahogany}\Sigma y^{2}})-({\color {BurntOrange}\Sigma y})^{2}]}}}$

Donde:

${\color {BrickRed}\Sigma xy}$ = Suma total de los valores multiplicados entre X e Y
${\color {Blue}\Sigma x}$ = Suma total de solamente los valores de X
${\color {Fuchsia}\Sigma x^{2}}$ = Suma total de los valores de X al cuadrado
${\color {BurntOrange}\Sigma y}$ = Suma total de solamente los valores de Y
${\color {Mahogany}\Sigma y^{2}}$ = Suma total de los valores de Y al cuadrado
${\color {Melon}n}$ = Número de valores tomados (en pares). Se puede determinar mediante
el número de filas cuando los datos se ordenan verticalmente y en pares.

• Dependiendo del resultado obtenido a través de la fórmula, se le asigna un grado de relación:

Valores	Relación
de    ± 0.80    a    ± 0.99	Muy alta
de    ± 0.60    a    ± 0.79	Alta
de    ± 0.40    a    ± 0.59	Moderada
de    ± 0.20    a    ± 0.39	Baja
de    ± 0.01    a    ± 0.19	Muy baja

Regresión lineal simple

Transcluido de Regresión y Correlación

Esta fórmula se utiliza para determinar la pendiente del gráfico.

Modelo de estimación:

${\hat {y}}={\color {Red}B_{o}}+{\color {OliveGreen}B_{1}}({\hat {x}})$

${\color {OliveGreen}B_{1}}={\frac {{\color {Melon}n}({\color {BrickRed}\Sigma xy})-({\color {Blue}\Sigma x})({\color {BurntOrange}\Sigma y})}{[{\color {Melon}n}({\color {Fuchsia}\Sigma x^{2}})-({\color {Blue}\Sigma x})^{2}]}}$

${\color {Red}B_{o}}={\bar {y}}-{\color {OliveGreen}B_{1}}({\bar {x}})$

Donde: ${\color {BrickRed}\Sigma xy}$ = Suma total de los valores multiplicados entre X e Y ${\color {Blue}\Sigma x}$ = Suma total de solamente los valores de X ${\color {Fuchsia}\Sigma x^{2}}$ = Suma total de los valores de X al cuadrado ${\color {BurntOrange}\Sigma y}$ = Suma total de solamente los valores de Y ${\color {Melon}n}$ = Número de valores tomados (en pares). Se puede determinar mediante el número de filas cuando los datos se ordenan verticalmente y en pares.

Donde: ${\color {OliveGreen}B_{1}}$ = Valor obtenido en la fórmula B1 ${\bar {y}}$ = Promedio de todos los valores de la variable Y ${\bar {x}}$ = Promedio de todos los valores de la variable X

Tipos de diagrama

Dispersión positiva o creciente

dispersión positiva

Dispersión positiva débil

Dispersión positiva débil

Dispersión negativa o decreciente

dispersión negativa

Dispersión negativa débil

dispersión negativa débil

Dispersión nula

Dispersión nula

Ejemplo

Un establecimiento desea ampliar el número de cajas que posee.

Se ha recolectado información del tiempo de espera de sus clientes y el número de cajas, los datos se muestran a continuación:

Tiempo de espera	Número de cajas
17.1	5
21.3	4
10.2	8
19.4	4

Desarrollo

1.   Se determina qué variable depende de otra.

Se puede usar la pregunta "¿Si Variable 1 aumenta, Variable 2 también lo hace?", si es correcto entonces Variable 1 es la variable independiente o la variable X.

2.   Se realiza un cuadro para determinar los valores que se usarán en la fórmula.

Tiempo de espera (Y)	Número de cajas (X)	XY	X²	Y²
17.1	5	85.5	25	292.41
21.3	4	63.9	9	453.69
10.2	8	81.6	64	104.04
19.4	4	77.6	16	376.36
_____________	_____________	_____________	_____________	_____________
68	20	308.6	114	1226.5

3.   Con los datos, reemplazar en la fórmula y determinar la correlación.

$r={\frac {{\color {Melon}4}({\color {BrickRed}308.6})-({\color {Blue}20})({\color {BurntOrange}68})}{\sqrt {[{\color {Melon}4}({\color {Fuchsia}114})-({\color {Blue}20})^{2}][{\color {Melon}4}({\color {Mahogany}1226.5})-({\color {BurntOrange}68})^{2}]}}}$
$r=-0.99$
La relación entre el Número de Cajas y el Tiempo de Espera es muy alta

4.   Con los datos, se procede a diagramar el gráfico.

Gráfica de dispersión

5.    Ahora, determinamos el modelo de regresión lineal y le añadimos la línea de regresión para determinar su correlación gráficamente.

${\hat {y}}={\color {Red}B_{o}}+{\color {OliveGreen}B_{1}}({\hat {x}})$

${\color {OliveGreen}B_{1}}={\frac {{\color {Melon}4}({\color {BrickRed}308.6})-({\color {Blue}20})({\color {BurntOrange}68})}{[{\color {Melon}4}({\color {Fuchsia}114})-({\color {Blue}20})^{2}]}}$ ${\color {OliveGreen}B_{1}}={\color {OliveGreen}-2.24}$

${\color {Red}B_{o}}=17-{\color {OliveGreen}-2.24}({\bar {5}})$ ${\color {Red}B_{o}}={\color {Red}28.2}$

• Por lo que se tiene que el modelo de estimación es...

$y={\color {Red}28.2}\;{\color {OliveGreen}-2.24}(x)$

Gráfica de dispersión con regresión